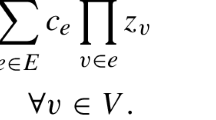Abstract.
We introduce the notion of a halfspace matrix, which is a sign matrix A with rows indexed by linear threshold functions f, columns indexed by inputs x ∈ {− 1, 1}n, and the entries given by A f,x = f(x). We use halfspace matrices to solve the following problems.
In communication complexity, we exhibit a Boolean function f with discrepancy Ω(1/n 4) under every product distribution but \(O(\sqrt{n}/2^{n/4})\) under a certain non-product distribution. This partially solves an open problem of Kushilevitz and Nisan (1997).
In learning theory, we give a short and simple proof that the statisticalquery (SQ) dimension of halfspaces in n dimensions is less than 2\((n + 1)^2\) under all distributions. This improves on the \(n^{O(1)}\) estimate from the fundamental paper of Blum et al. (1998). We show that estimating the SQ dimension of natural classes of Boolean functions can resolve major open problems in complexity theory, such as separating PSPACE \(^{cc}\) and PH \(^{cc}\).
Finally, we construct a matrix \(A \in \{-1, 1\}^{N \times N^{\text{log} N}}\) with dimension complexity logN but margin complexity \(\Omega(N^{1/4}/\sqrt{\log N})\). This gap is an exponential improvement over previous work. We prove several other relationships among the complexity measures of sign matrices, omplementing work by Linial et al. (2006, 2007).
Similar content being viewed by others
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript received 28 August 2007
Rights and permissions
About this article
Cite this article
Sherstov, A.A. Halfspace Matrices. comput. complex. 17, 149–178 (2008). https://doi.org/10.1007/s00037-008-0242-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00037-008-0242-4
Keywords.
- Linear threshold functions
- communication complexity
- complexity measures of sign matrices
- complexity of learning