Symmetry-induced ambiguity in orientation estimation from RGB images

Abstract

The estimation of object orientation from RGB images is a core component in many modern computer vision pipelines. Traditional techniques mostly predict a single orientation per image, learning a one-to-one mapping between images and rotations. However, when objects exhibit rotational symmetries, they can appear identical from multiple viewpoints. This induces ambiguity in the estimation problem, making images map to rotations in a one-to-many fashion. In this paper, we explore several ways of addressing this problem. In doing so, we specifically consider algorithms that can map an image to a range of multiple rotation estimates, accounting for symmetry-induced ambiguity. Our contributions are threefold. Firstly, we create a data set with annotated symmetry information that covers symmetries induced through self-occlusion. Secondly, we compare and evaluate various learning strategies for multiple-hypothesis prediction models applied to orientation estimation. Finally, we propose to model orientation estimation as a binary classification problem. To this end, based on existing work from the field of shape reconstruction, we design a neural network that can be sampled to reconstruct the full range of ambiguous rotations for a given image. Quantitative evaluation on our annotated data set demonstrates its performance and motivates our design choices.

1 Introduction

A core component in many modern computer vision pipelines is pose estimation. Pose estimation is the process of predicting the position and orientation (pose) of objects in images, relative to the camera. This information allows, e.g., a robotic system to build an internal map of its surroundings, capturing where objects are in relation to itself. In turn, this allows the system to approach, grab, avoid, or otherwise interact with objects in its environment. Though the performance of recent works on pose estimation has been impressive, there are still a number of key challenges to overcome [1, 2]. One such challenge, which has seen an increased amount of attention in recent years, is the influence of ambiguity. More specifically, some objects may appear visually identical from different viewpoints, causing images to map to poses in a one-to-many fashion. This phenomenon mainly occurs as a consequence of symmetries that can be present in the observed object, or be induced by self-occlusion or occlusions caused by the environment. Moreover, in some cases, the environment cannot be controlled, and objects can appear in uncertain configurations. Examples of such tasks include autonomous driving [3], collaborating with humans [4], and robotic grasping of objects in dynamic environments [5, 6].

Traditionally, pose estimation techniques have been designed to predict only a single output pose. As such, these methods fail to report the multitude of possibly correct poses for symmetric objects. Moreover, when approached naively, the presence of ambiguities can be detrimental to the performance of single-output techniques. Deep neural networks, which are common-place in pose estimation, are known to minimize the penalty between their single prediction and all ambiguous poses appearing in the data set. As a consequence, such networks will converge to a conditional average pose, which renders them often meaningless for this situation.

Recent works have addressed symmetry-induced ambiguity to various degrees. Methods in the first category aim to prevent symmetries from disturbing the training process of neural networks. One approach is to apply canonicalization of symmetric poses, mapping all symmetric poses to a single canonical pose [7,8,9]. However, this approach requires upfront knowledge about the exact symmetries present in objects, which becomes infeasible when considering the complex ambiguities caused by occlusions. A different approach is to apply symmetry-aware loss functions, like the ShapeMatch-Loss [10], which uses a polygonal mesh to automatically identify symmetric poses. Nevertheless, this loss cannot deal with symmetry-breaking textures or induced symmetries. Furthermore, since only a single pose is predicted, no information about possible ambiguities can be deduced from the output, which would be valuable in downstream tasks like robotic grasping and next-best view prediction.

A more recent, second category of works addresses symmetry-induced ambiguity indirectly as a cause of uncertainty. When considering a probability distribution over the possible poses for an observed object, symmetric poses appear as equally probable outputs. Several recent works have used Bingham distributions [11,12,13], Von Mises distributions [14], and Matrix Fisher distributions [15] to output such distributions. While these methods are indirectly able to predict multiple poses, their distributions require computationally expensive normalization and complex parameterizations. Moreover, the choice of distributions limits the expressivity of the algorithm. Non-parametric distributions can address this issue [16, 17], but often require discretization over the space of poses.

As part of the second category, inspired by recent advances in implicit shape reconstruction [18], Murphy et al. [19] propose to encode a probability density function in a shallow fully-connected neural network. In doing so, they provide a non-parametric output density that can take arbitrarily complex shapes, and does not require discretization of the space of poses. Sampling from the distribution, however, still requires the brute force computation of a normalization constant by means of sampling a grid of poses.

Though recent work has addressed symmetry-induced ambiguity, we improve upon these results by exploring different ways of performing pose estimation on symmetric objects. Specifically, given a single RGB image, our goal is to predict not just a single correct pose, but rather a range of multiple possibly correct poses under symmetry-induced ambiguity. However, we note that rotational symmetries are the most common source of ambiguity in pose estimation. Therefore, we do not perform full 6D pose estimation, but rather focus on the subproblem of orientation estimation. Finally, no prior knowledge on the types of symmetries present in observed objects is assumed to be available, and our method should be able to work with inherent symmetries as well as induced symmetries.

Towards this goal, we propose to model orientation estimation as a binary classification problem: rather than predicting rotations directly, or predicting a normalized distribution over rotations, our model instead predicts whether an object in a given rotation could have resulted in a given image. The model can be sampled to reconstruct the full range of ambiguous rotations for a given image. Predictions can be interpreted directly and do not require expensive normalization. We also provide new annotations for part of the recently introduced SYMSOL II data set [19]. For every recreated image, we provide the complete set of possible orientations when considering rotational symmetries. In doing so, we create the first orientation estimation data set with annotated symmetry information, covering symmetries induced through self-occlusion.

2 Preliminaries

This section introduces the main concepts and provides some background information.

2.1 Symmetries in 6D object pose estimation

The problem of pose estimation is to determine the pose of an object relative to a camera, given some RGB image of that object. Position can be represented by a vector $t \in \mathbb {R}^{3}$, giving the translation relative to the camera. Moreover, orientation can be represented by a rotation matrix $R \in SO(3),$ representing a rotation with respect to the camera frame. Together, the translation and rotation yield six degrees of freedom and are referred to as the 6D pose of an object. Hence the name—6D pose estimation.

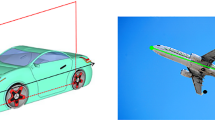
One of the main complexities in pose estimation is symmetry. In practise, many objects exhibit rotational symmetries, making them appear identical from different viewpoints. Several types of rotational symmetries can be distinguished. Firstly, symmetries can be discrete or continuous. A cube, for example, has a discrete number of symmetric orientations, while a cylinder has a continuous symmetry about its central axis, see Fig. 2b. Moreover, we distinguish between symmetric objects and nearly symmetric objects. Symmetric objects have global symmetries, that are inherent to the object. In contrast, nearly symmetric objects have a symmetry breaking feature, meaning they have no inherent symmetries. Nevertheless, if the symmetry breaking feature becomes occluded, a symmetry can be induced (Fig. 1). In pose estimation, these symmetries result in orientation ambiguity, as multiple rotations result in the same observed image. Therefore, in the presence of symmetries, images can map to poses in a one-to-many fashion.

Fig. 1

Nearly symmetric objects, like mugs, can appear symmetric under occlusion. Consequently, they can produce single-valued symmetry sets (a) or multi-valued symmetry sets (b) depending on the view

This mapping is formalized in what are called symmetry sets [20]. For an image showing an object of interest, there exists a set of poses, for which the shape and appearance of the object projected on the image are indistinguishable across the poses. This set of poses is referred to as the symmetry set of the image. Let $\mathcal {I}$ be the space of all images, then the symmetry set of an image $I \in \mathcal {I}$ is defined as

$$\begin{aligned} S_{SE(3)}(I) = \left\{ (t, R) \in SE(3): \mathcal {R}(t, R) = I \right\} .\end{aligned}$$

(1)

here $\mathcal {R}$ is defined as an abstract ‘rendering’ function $\mathcal {R}: SE(3) \rightarrow \mathcal {I}$, which can take a 6D pose and produce an image. Many details are abstracted in this function, such as the geometry of the rendered object, lighting conditions, and other environment variables. Importantly, we assume that the object of interest is visible in I. If it were not visible, an S(I) would contain an infinite number poses, all of which would transform the object outside the view of the camera.

Dealing with the ambiguity caused by these rotational symmetries is the prime focus of our work. Since rotational symmetries only pertain to orientation, we restrict the pose estimation problem to orientation estimation. More specifically, instead of estimating full 6D poses, we assume the translation is fixed, and only predict orientation. In this context, the definition of a symmetry set, used throughout the paper, becomes

$$\begin{aligned} S(I) = \left\{ R \in SO(3): \mathcal {R}(R) = I \right\} \,\end{aligned}$$

(2)

where $\mathcal {R}$ is defined only over the rotation manifold $\mathcal {R}: SO(3) \rightarrow \mathcal {I}$.

Fig. 2

A cube (a) has a discrete number of symmetric orientations. In contrast, a cylinder (b) yields continuous symmetry for rotations around its central axis. Axes of symmetry are shown as dashed lines

2.2 Uncertainty and ambiguity

Though there are many different ways of performing pose estimation, most modern methods rely on deep learning. Large data sets of images with annotated object poses are used to train neural networks. When considering the robustness of a neural network, uncertainty is a commonly-used term. When a network produces output, it is desirable for that output to be accompanied by some measure of certainty, such that the quality of the output can interpreted before it is put to use. For example, if an input is given to a network, which is completely unlike any of the inputs used during training, the network may produce incorrect output. In pose estimation, this can occur when, e.g., an object appears under different lighting conditions in the real world compared to the training data. In this case, it is desirable for the network to present its output with low confidence.

Symmetry in pose estimation is often addressed as a source of uncertainty. When an image can map to multiple different poses, any individual pose should be output with low confidence. After all, the network is uncertain as to which of the poses in the symmetry set is correct. However, this interpretation only holds for models that output a single pose. In contrast, if a model properly represents the one-to-many mapping between images and poses, symmetries do not have to cause uncertainty. If a given image closely resembles the training set, a network could output all possible symmetries with high confidence.

To avoid confusion, it is important to understand the difference between ambiguity and uncertainty. Ambiguity is an inherent property of the problem domain. An image can map to multiple poses, making the problem of pose estimation ambiguous. Uncertainty, on the other hand, is an emergent property of the neural network and its training process. When a network is unable to make a prediction with high confidence, we speak of uncertainty. Ambiguity can be a source of uncertainty if the network is ill-equipped to deal with it. However, if the model is designed with the ambiguity in mind, a high degree of ambiguity can exist without any uncertainty.

2.3 Axis-angle representation

Besides rotation matrices, another useful way of representing rotations is as an axis-angle pair. Following Euler’s rotation theorem, every 3D rotation can be represented as a rotation around a single axis [21]. Therefore, any rotation can be described by a pair $(n, \alpha )$, where n is a unit vector in $\mathbb {R}^3$ and $\alpha \in [0, 2 \pi )$, which describes a rotation by $\alpha$ radians around axis n. Alternatively, rotation vectors offer a more compact representation, taking the angle $\alpha$ and encoding it in the magnitude of n. A rotation is then described by a single vector $n' \in \mathbb {R}^3$, with $|n'| \in [0, \pi ]$, which represents a rotation of $|n'|$ radians around the axis codirectional with $n'$.

Note how the angle of rotation is now restricted to a maximum of $\pi$ radians. This is, however, no restriction in the expressivity of rotation vectors, since a rotation of $-\alpha$ radians around an axis n is equal to a rotation of $\alpha$ radians around the axis $-n$. An important consequence of this is the equivalence between the rotation vectors $n'$ and $-n'$ when $|n'| = \pi$, which makes the mapping from SO(3) to rotation vectors ambiguous. Nevertheless, with this antipodal symmetry taken into account, rotation vectors are particularly useful for visualization, since they lie completely in $\mathbb {R}^3$. As rotation vectors occupy a ball with radius $\pi$ and its center on the origin, a plot of rotation vectors is called a $\pi$-ball plot. Figure 3 shows several examples. Note how rotations around the same axis, with respect to the identity rotation, appear on a straight line 3a. In contrast, rotations around the same axis with respect to a different reference frame can occur as arcs (3c).

Fig. 3

Examples of $\pi$-ball plots showing rotation vectors. Each plot shows 20 rotations around the x-, y-, and z-axis of a different local reference frame. For each axis, the 20 rotations have their rotation angles equally spaced from 0 to $2\pi$ radians. Rotations around the x-, y-, and z-axis are colored red, green, and blue respectively. In plot (a), all rotations are relative to the identity rotation, which lies at the origin. In plot (b), the local reference frame is rotated by $\frac{\pi }{2}$ radians around the z-axis relative to the identity. In plot (c), the local reference frame is further rotated by $\frac{\pi }{2}$ radians around the x-axis relative to (b)

3 Related works

Symmetry-induced ambiguity has been addressed by recent works to varying extents. Among these, most related to our proposed method, is the category of works addressing ambiguity under the broader concept of uncertainty. The most prominent line of work in this direction aims at outputting probability distributions over poses, rather than predicting poses directly. More specifically, given an image, the conditional distribution over poses given the image is predicted. In this setting, symmetry- induced ambiguity manifests as multiple output poses with equal probability in the conditional distribution. An accurate estimation of this distribution could, therefore, be used to detect and explain symmetries present in an image. We distinguish between methods that output parametric and non-parametric distributions.

3.1 Parametric distributions

One option is to use parametric distributions from directional statistics to estimate the conditional pose distribution. The benefit of having a small set of parameters is that they are easily interpretable and can be estimated by a neural network directly. Multiple such distributions have been used by recent works including the Von Mises distribution [14], Bingham distribution [11,12,13], and Matrix Fisher distribution [15]. Both the Bingham and Matrix Fisher distributions require the computation of a normalizing constant during training, requiring expensive interpolation [11, 13] and approximation [15] schemes.

While Mohlin et al. [15] output the parameters of a single Matrix Fisher distribution, others have moved in the direction of outputting mixtures of multiple distributions. The latter allows for estimating multimodal distributions, which are a common occurrence when symmetry-induced ambiguities are involved. Prokudin et al. [14] show how to construct a mixture model with an infinite number of mixing components using a conditional variational autoencoder (CVAE). Their architecture is based on biternion networks [22], which output 2D rotations in the form of 2D vectors $(\cos (\varphi ), \sin (\varphi ))$, where $\varphi$ is an angle of rotation. These vectors are coined biternions in [22], and correspond to unit quaternions around a fixed reference axis. Hence, the CVAE can only predict 2D poses, and is applied to 2D head pose estimation in the paper. Nevertheless, the authors do create a 3D implementation, where each axis is predicted separately. Deng et al. [13] propose Deep Bingham Networks (DBNs), which output parameters for a mixture of Bingham distributions. Mode collapse is prevented by using a ‘Winner Takes All’ (WTA) strategy during training.

While these parametric distributions form a convenient and interpretable output format for neural networks, their expressiveness is limited. By choosing a specific distribution, or mixture thereof, an assumption is made on the shape of the conditional pose distribution. In the presence of symmetry-induced ambiguity, the conditional distribution is uniform over all symmetric poses and is often multimodal. However, all the aforementioned techniques struggle to accurately represent this uniformity, as they use non-uniform priors.

3.2 Non-parametric distributions

Non-parametric distributions provide an alternative that does not make assumptions on the shape of the predicted distribution. As such, they have the potential to more accurately represent the complex conditional pose distributions caused by symmetries. We highlight three important works from this category.

Deng et al. [17] use a Rao-Blackwellized particle filter to track the posterior distribution over object poses over time. To this end, the posterior is decomposed into separate translation and rotation components. The space of rotations is discretized into 191 thousand bins and the likelihood of a given discretized pose with respect to a given observation is determined by code-book matching. An augmented auto-encoder [23] is used to this end, which embeds observed and pre-rendered images into a shared embedding space, in which similarity scores can be computed. Poor translation estimates also result in poor similarity scores, in turn allowing for the computation of likelihoods for translation hypotheses.

Okorn et al. [16] similarly use code-book matching to create a discretized non-parametric histogram distribution over rotations. Rather than using an auto-encoder, they instead learn a comparison function between features of pre-rendered images and observed images. Likelihoods can be computed for each of the discretized rotations by inferring this learned similarity metric. These likelihoods can, furthermore, be interpolated to create a continuous distribution.

A more recent method, known as OVE6D [24], utilizes an encoder to generate embeddings that indicate similarity in orientation as well. In this approach, in-plane orientations are disregarded initially and computed efficiently at a later stage in the pipeline. This methodology enables the use of a reduced set of templates, decreasing storage size and computation time.

Another intriguing method [25] uses representation learning to evaluate orientations by employing two distinct encoders. One for query images (the RGB-encoder) and one for proposed orientations (the SO(3)-encoder). Both encoders map their inputs to a space where proximity indicates similarity in projection. To achieve this, the SO(3)-encoder is trained to generate an encoding with the same values as the RGB-encoder would for an image where the given rotation was applied to the target object.

Regression-based methods minimize pose discrepancy by selecting the closest candidate within a set of ambiguous poses [26] or regressing to a predefined set of geometric features based on symmetry annotations [27].

Most recently, Hsiao et al. [28] introduced a score-based diffusion method to solve the pose ambiguity problem in RGB-based object pose estimation. Although the method shows superior accuracy and effectiveness in resolving pose ambiguity encountered in 6D object pose estimation, it has difficulties with occlusions caused by the environment and/or the object itself.

Implicit-pdf [19] takes a rather different approach. The authors estimate conditional rotation distributions as un-normalized functions over the combined space of images and rotations, which can be parameterized by a neural network. The architecture is divided into two conceptual stages, where the first embeds images into feature vectors using a CNN, and the second concatenates such an embedding with an encoded rotation matrix, which is fed into a shallow fully connected network. The small size of the second stage allows for efficiently evaluating multiple sample rotations for a single image. Using these samples, a normalizing constant can be approximated, which is used to turn the un-normalized output into a proper probability distribution.

As discussed above, implicit-pdf does not require discretizing the rotation space. Moreover, the predicted probability distribution can be inferred using the full expressive power of a multi-layer neural network. Hence, it can be almost arbitrarily complex. These desirable features make implicit-pdf one of the primary groundworks for our propsed classification model.

3.3 Multiple-hypothesis prediction

Manhardt et al. [20] take a different approach. They propose a model that produces multiple pose hypotheses for a single image. To this end, they train a network with duplicated output layers using a ‘Winner Takes All’ strategy. The range of predicted hypotheses can be interpreted as a Bingham distribution. How close the hypotheses lie together, moreover, serves as an indication of the presence of ambiguity. More specifically, if there is no ambiguity, all hypotheses will lie close together. If there is ambiguity, the hypotheses will be spread out. By performing further analyses, the axis of symmetry can even be reconstructed from a set of hypotheses.

Compared to the other works mentioned above, these multiple-hypothesis prediction (MHP) models come with a desirable set of properties. They neither require complex parameterization, nor the manual canonicalization of poses before or during the training process. Moreover, they are able to directly predict a set of multiple, possibly symmetric, poses.

4 Method

In this section we propose a new network design in which we model orientation estimation as a binary classification problem.

4.1 Binary classification

Unlike methods which represent symmetry-induced ambiguity by predicting probability distributions over SO(3), we represent symmetry sets implicitly through a classifier. That is, a model would not output (a discrete set of) rotations directly, but instead classify a given rotation as being part of the symmetry set or not, when conditioned to a given image. More formally, we wish to find a classifier

$$\begin{aligned} \mathcal {C}: SO(3) \times \mathcal {I} \rightarrow \{0, 1\} \,\end{aligned}$$

(3)

which takes a rotation R and an image I as inputs, and classifies whether or not $R \in S(I)$. Assuming such a classifier $\mathcal {C}$ exists, it is easy to see how it would facilitate the reconstruction of symmetry sets. Note how the classifier accepts the full space of SO(3) as an input domain. Hence, for a given image I, $\mathcal {C}$ can be queried with an arbitrary number of rotations sampled at a continuous resolution. Consequently, S(I) can be reconstructed at arbitrary resolution, e.g., in as far as computational constraints allow.

Furthermore, the existence of $\mathcal {C}$ would also facilitate convenient sampling of intersections of symmetry sets. Let $I_i \in \mathcal {I},$$1 \le i \le N,$ be images of the same object, but taken from different view points. Moreover, assume that rotations in the symmetry sets for all images are defined relative to some common frame of reference. Then, as mentioned before, the intersection $\bigcap _{i=1}^{N} S(I_n)$ gives the set of rotations that fit all observations. Note that a given rotation $R \in SO(3)$ is in this set if and only if it is in each of the separate symmetry sets. More formally,

$$\begin{aligned} R \in \bigcap _{i=1}^{N} S(I_i) \iff \bigwedge _{i=1}^{N} R \in S(I_i) .\end{aligned}$$

(4)

Assuming $\mathcal {C}$ to be a perfectly accurate classifier, we could test whether R is in the symmetry set of an image image $I_i$ by checking $\mathcal {C}(R, I_i) = 1$. Therefore, R is in the intersection if and only if $\bigwedge _{i=1}^{N} \mathcal {C}(R, I_i) = 1$.

The rest of this section details how such a classifier $\mathcal {C}$ can be parameterized by a neural network. The design is based on that of occupancy networks, which will be explained first.

4.2 Review on occupancy networks

The idea we propose is closely related to recent works in 3D shape reconstruction, as well as the work by Murphy et al. [19]. In 2019, both Mescheder et al [18] and Chen et al. [29] presented similar works in which 3D shape reconstruction is modeled as a binary classification problem. Both note how a shape can be seen as the set of all points $p \in \mathbb {R}^3$ that are located within the boundaries of the object. In other words, the object occupies all such points $p \in \mathbb {R}^3$. Hence, shapes can be described by a so-called occupancy function

$$\begin{aligned} o: \mathbb {R}^3 \rightarrow \{0, 1\} \,\end{aligned}$$

(5)

which classifies whether a given point is occupied by the object or not. Now, given an image $I \in \mathcal {I}$, the shape of the object in I can be output as an occupancy function. While the idea is quite simple, it is not immediately clear how to output such an occupancy function.

The solution proposed in [18, 29] is to replace the discrete output domain $\{0, 1\}$ of the occupancy function, by the interval [0, 1]. Values in this range are then interpreted as probabilities, such that the output represents the probability that a given point is occupied by the object. By setting a threshold $\mathcal {T}$, a mapping can then be made back to the original classification domain. Furthermore, rather than creating a separate mapping from images to occupancy functions, the two stages are merged into a single function, i.e.,

$$\begin{aligned} f: \mathbb {R}^3 \times \mathcal {I} \rightarrow [0, 1].\end{aligned}$$

(6)

In this formulation, function f directly evaluates the occupancy for a given point $p \in \mathbb {R}^3$ with respect to the object in a given image $I \in \mathcal {I}$. Now, f is in the traditional form of classification problems used in deep learning and can be approximated by a neural network. Mescheder et al. call such a network an Occupancy Network.

4.3 Application to orientation estimation

With the concept of occupancy networks briefly presented, we revisit the formulation of pose estimation as a binary classification problem. At first glance, the context of 3D shape reconstruction seems completely different from orientation estimation. However, we can draw parallels between the two, where the reconstruction of symmetry sets is analogous to a shape reconstruction problem on the rotation manifold.

4.3.1 Shapes of symmetry sets

Analogous to how an object can be seen as a set of 3D points, which together occupy bounded regions in Euclidean space, a symmetry set can be seen as a set of rotations, which together occupy bounded regions on the surface of the rotation manifold. The most notable difference is the input space. In contrast to objects, symmetry sets are constrained to the rotation manifold.

Hence, an occupancy function describing a symmetry set can be formulated as

$$\begin{aligned} o: SO(3) \rightarrow \{0, 1\} .\end{aligned}$$

(7)

Fig. 4

Different types of symmetries correspond to differently-shaped symmetry sets. Discrete symmetries (left) yield symmetry sets consisting of singular points, continuous symmetries around a single axis (middle) trace a continuous loop, and continuous multi-axial symmetries (right) trace a volume. Though symmetry sets are actually defined on the rotation manifold, a simplified 3D interpretation is depicted here for clarity

Whereas objects typically occupy a single continuous volume in $\mathbb {R}^3$, symmetry sets can take on very different shapes. We note how different types of symmetries result in symmetry sets with different properties. Interpretations of this effect are depicted in Fig. 4. If an image I depicts an object with discrete symmetries, then S(I) will be a finite set. Moreover, the elements of S(I) likely lie apart, thus creating a finite number of disconnected singular points on the rotation manifold. If instead I depicts an object with a continuous symmetry, S(I) will be an infinite set and trace a continuous shape over the manifold. In this case, two notable cases can be distinguished: the object is symmetric (i) around a single axis, or (ii) around multiple. Take for example a cone, which is symmetric only around a single axis. In this case, S(I) traces a continuous loop around SO(3). Importantly, however, this loop is infinitely thin, causing it to have zero volume. Only when the object has a continuous multi-axial symmetry, will the symmetry set occupy a patch with non-zero volume. Corona et al. [30] proved that such multi-axial symmetries only occur for spheres, making them very rare in practice. Their proof only pertains to global symmetries, however, and does not cover occlusion-induced symmetries. Nevertheless, we conjecture that multi-axial symmetries can only be induced if an object appears like a perfect sphere under some occlusion.

Since discrete and single-axis symmetries are very common, the shapes of symmetry sets often consist of thin structures. For such structures to be accurately modeled, the occupancy function must produce sharp peaks. However, recent analyses [31] has shown that the high frequencies required to produce these peaks are difficult to model using an MLP. This will be an important consideration when designing an occupancy network for modeling symmetry sets.

4.3.2 Network design

With the above analogy to 3D shape reconstruction, we can apply the concept of an occupancy network to orientation estimation. Our network design is based on that of occupancy networks and is heavily inspired by the design of Murphy et al. [19]. Conceptually, we use a two-stage process. The first stage extracts features from a given image, embedding it into a low-dimensional vector. The second stage uses the embedding in combination with a given rotation to evaluate an occupancy function on SO(3), conditioned on the image, see Eq. (7). Similar to Eq. (6), these two stages are combined into a single function formulated as

$$\begin{aligned} f_{\theta }: SO(3) \times \mathcal {I} \rightarrow [0, 1]\,\end{aligned}$$

(8)

parameterized by a neural network with parameters $\theta$. Note that the output domain is changed from $\{0, 1\}$ to [0, 1] to fit the traditional formulation of a binary classification problem. An output value can be interpreted as the probability that a given rotation $R \in SO(3)$ is in the symmetry set S(I) of a given image $I \in \mathcal {I}$.

4.3.3 Representing rotations

Our formulation operates on rotations instead of 3D Euclidean coordinates. In practice, this requires picking a suitable representation for rotations to be used as inputs for the neural network.

Following conclusions by Murphy et al. [19] who tested various rotation representations, we pick orthogonal matrices for representing input rotations, thus changing the formulation in Eq. (8) to

$$\begin{aligned} f_{\theta }: \mathbb {R}^9 \times \mathcal {I} \rightarrow [0, 1].\end{aligned}$$

(9)

4.3.4 Positional encoding

To address the issue of thin shapes common in symmetry sets, we apply a Positional Encoding (PE) to all input rotations before feeding them to the MLP. As mentioned in Sect. 4.3.1, MLP networks have been shown to have difficulties learning high frequency functions, which have sharp local fluctuations [31]. Nevertheless, to properly represent thin symmetry sets, we require our MLP to produce sharp peaks in the occupancy function.

Recent work has addressed this issue by manually mapping input values to vectors in a higher dimensional space using high frequency functions. The resulting vector is then used as input to the network instead. Mildenhall et al. [32] first showed how this technique helped in reconstructing fine details in shapes. Murphy et al. [19] have subsequently shown its successful application to input rotations. The most popular mapping applies a function $\gamma: \mathbb {R} \rightarrow \mathbb {R}^{2F}$, defined as

$$\begin{aligned} \gamma (x)&= \bigg ( \sin \left( 2^0 \pi x \right), \cos \left( 2^0 \pi x \right), \cdots \nonumber \\&\quad \sin \left( 2^{F - 1} \pi x \right), \cos \left( 2^{F-1} \pi x \right) \bigg ) \,\end{aligned}$$

(10)

where $x \in \mathbb {R}$, and F is the number of frequencies. Higher values of F exponentially increase the frequency with which inputs are embedded. Furthermore, note that $\gamma$ is applied to individual input values. In our use-case, that means $\gamma$ is applied separately to each of the 9 values making up an input rotation matrix. Therefore, we effectively create a mapping from $\mathbb {R}^9$ to $\mathbb {R}^{9 \cdot 2F}$.

Fig. 5

Schematic overview of the occupancy network used to reconstruct symmetry sets; see text for details

4.3.5 Final design

Putting everything together, we arrive at the architecture described in Fig. 5. Images are first embedded into a lower-dimensional vector of size E using a pre-trained ResNet model. The embedding is subsequently concatenated with the positional encoding of a query rotation, and fed to an MLP model. Note that the positional encoding contains $9 \cdot 2F$ values, since Eq. (10) contains both a sine and a cosine for each frequency. This makes the total combined input size for the MLP model $E + 9 \cdot 2F$. Finally, the output of the MLP model is passed through a Sigmoid function, which ensures that its value lies in the domain [0, 1].

4.3.6 Training strategy

When applying the training process of a traditional occupancy network to the proposed network a problem appears, since both positive and negative samples are required to train a classifier. Specifically, the training data must cover examples of both occupied and unoccupied points. In the occupancy network, these samples are provided by randomly sampling points inside the bounding volume of an object and testing whether they lie inside or outside the object shape. This is possible because the shape of the object is known through a provided CAD model. The problem appears when we try to do the same for symmetry sets. Random samples cannot be checked to lie inside or outside the symmetry set, because no ground truth representation of the symmetry set is assumed to be available. Unlike object shapes, which are relatively easy to recreate using 3D modeling tools, symmetry sets are too difficult to annotate. In the presence of self-occlusion, for example, the exact shapes of symmetry sets can vary dramatically from one image to the next. It is in fact this very complex relationship between images and symmetry sets that motivated the design of the network in the first place.

The only data that we assume to be available during training consists of image-rotation pairs, where each image is annotated only with the corresponding ground truth pose. In terms of a classification problem, this means only a single, positive sample is available for each image. More formally, such a data set $\mathcal {D}$ can be described as

$$\begin{aligned} \mathcal {D} = \left\{ (I_i, R_i): 1 \le i \le N, I_i \in \mathcal {I}, R_i \in SO(3) \right\} \,\end{aligned}$$

(11)

where N denotes the number of pairs in the data set. With only this information, training the proposed network like an occupancy network seems impossible. Nevertheless, we find that by restricting the supported types of symmetries to only discrete and continuous single-axis, a training strategy for the proposed network can be formulated using only image-rotation pairs.

4.3.7 Restricting to discrete and single-axis symmetries

The proposed training strategy relies on a particular property of discrete and single-axis symmetries, namely that they have zero volume on the rotation manifold. As a consequence, an image I that exhibits an object with only a discrete or continuous single-axis symmetry, or a combination thereof, will produce a symmetry set with zero volume. Hence, a random rotation $R_i$ sampled uniformly from SO(3) falls inside S(I) with probability zero. It can, therefore, be assumed that for any such $R_i$ it holds that $R_i \notin S(I)$.

With this key observation, we turn back to the training process of our occupancy network. It is no longer necessary to have annotated ground truth symmetry sets, now that any randomly sampled rotation is known to fall outside the symmetry set.

This is also problematic, since the network would only be given negative samples. We address this as follows. Rather than using only randomly-sampled rotations, we additionally evaluate the network at the ground truth rotation. Given an image-pose pair (I, R), this means R is manually added along side with K randomly-sampled rotations, in order to introduce a positive sample. More formally, we define the loss for a single image-rotation pair to be

$$\begin{aligned} \mathcal {L}(I, R) = H \left( f_{\theta }(I, R), 1 \right) + \sum _{i=1}^{K} H \left( f_{\theta }(I, R_i), 0 \right) \,\end{aligned}$$

(12)

where H refers to the binary cross-entropy loss function

$$\begin{aligned} H(o', o) = - o \log (o') - (1-o) \log (1 - o') .\end{aligned}$$

(13)

Note that $o = 1$ results in the second term becoming zero and $o = 0$ results in first term becoming zero. Hence, Eq. (12) can be rewritten to

$$\begin{aligned} \mathcal {L}(I, R) = - \log \left( f_{\theta }(I, R) \right) + \sum _{i=1}^{K} - \log \left( 1 - f_{\theta }(I, R_i) \right) .\end{aligned}$$

(14)

Fig. 6

Parameters from a trained multiple-hypothesis prediction (MHP) network can be used as pre-trained weights for the first stage of a binary classification model

4.3.8 Pre-training the first stage

Initial experiments using the loss from Eq. (14) showed inconsistent results. During training, the network has a tendency get stuck in a local optimum. More specifically, it gets stuck outputting 0 for all inputs. Considering Eq. (14), this strategy achieves an optimal score on all K negative samples, at the expense of very poor score on the ground truth rotation.

Further experimentation has showed that pre-training the first stage of the proposed network as a multiple-hypothesis prediction (MHP) model [20] helped to increase robustness; see also Fig. 6. A quantitative evaluation to substantiate this claim is presented in Sect. 5.6.1. For more details on MHP models and their appjlication to orientation estimation, we refer the reader to the supplementary material.

5 Evaluation

This section details experiments that evaluate the newly proposed binary classification network for orientation estimation.

5.1 Data set

To evaluate the proposed model, a data set is required that covers objects with different types of symmetries, and only pertains to orientation estimation. Furthermore, each image in the data set should be annotated with a single ground truth orientation for training, but also its full ground truth symmetry set for evaluation. Since the proposed model is specifically designed to reconstruct symmetry sets, its quality can not properly be evaluated without full annotations. Additionally, the proposed binary classification model makes an additional assumption that further constrains the data set. Namely, all objects can only exhibit discrete symmetries or single-axis symmetries. In practise, this excludes spheres, or objects that can appear perfectly spherical under occlusion. Since such objects are quite rare, this additional requirement is not particularly restrictive.

Considering the requirements above, we choose the SYMSOL data set proposed by Murphy et al. [19] for evaluation. It contains two subsets: SYMSOL I and SYMSOL II, covering symmetric and nearly-symmetric objects, respectively. The objects are synthetically-rendered and placed in the center of each image, thus ignoring translation. Objects are observed from a stationary camera, under constant lighting. Though the complexity of the objects and their presentation is limited in SYMSOL, the relation between viewpoint and symmetry set is still intricate due to occlusion-induced symmetries. Hence, we believe that an evaluation using this data set properly emphasises the models ability to reconstruct symmetry sets, rather than its ability to locate objects in visual clutter.

Full symmetry set annotations¹ are provided for SYMSOL I, but not for SYMSOL II. Hence, we present a recreation of marked tetrahedron and marked cylinder data sets with computed symmetry sets for every image. To achieve this, we exploit the known symmetries of the corresponding shapes without markings and apply a process for accepting or rejecting candidate orientations to form symmetry sets. For more details on this process we refer to the supplementary material. Note that we do not cover the marked sphere data set, as it contains multi-dimensional symmetry sets. Examples are shown in Fig. 7.

Fig. 7

Example symmetry sets from the annotated recreation of SYMSOL II. Images are shown with their respective symmetry sets in $\pi$-ball plots

5.2 Classification setup

The proposed model predicts whether a given rotation belongs or not to the symmetry set of a given image. This makes the model a function over the combined space of rotations and images, i.e.,

$$\begin{aligned} f_{\theta }: SO(3) \times \mathcal {I} \rightarrow [0, 1] .\end{aligned}$$

(15)

However, when considering only a single image $I \in \mathcal {I}$, we are left with a classification problem solely over SO(3). In this context, the network predicts whether a given rotation is inside the symmetry set S(I). Therefore, conceptually, every image is associated with its own instance of a classification problem over just the space of SO(3). For a fixed image I, the model becomes a function

$$\begin{aligned} f_{\theta }^{I}: SO(3) \rightarrow [0, 1] .\end{aligned}$$

(16)

For the rest of this evaluation, we measure the performance of the proposed model on a per-image basis, and compute average metrics over all images in the data set.

Since the proposed model predicts two classes, we can evaluate its performance using established metrics for evaluating binary classification models. To this end, it is productive to formulate our problem in the terminology used in the related literature. Consider the model as a classifier

$$\begin{aligned} \mathcal {C}_{\theta }^{I}: SO(3) \rightarrow \{0, 1\} \,\end{aligned}$$

(17)

for a fixed image $I \in \mathcal {I}$. This model is said to classify samples from SO(3) into two classes: the positive class (1) and the negative class (0). Here, a sample $R \in SO(3)$ is said to be in the positive class when $R \in S(I)$, and in the negative class when $R \notin S(I)$. Note, however, that our network does not predict this class directly, but rather outputs the probability of a sample being positive. To convert this output probability to a binary prediction, we set a probability threshold $\mathcal {T}$, such thatNow, to evaluate a model’s performance on an image, we take a set of samples for which their classes are known and compare them to predictions made by the model.

5.3 Evaluation metric

To evaluate the results, we use the popular F-measure, i.e.,

$$\begin{aligned} \mathcal {F} = 2 \cdot \frac{\mathcal {R} \cdot \mathcal {P}}{\mathcal {R} + \mathcal {P}} \,\end{aligned}$$

(18)

defined as the harmonic mean of recall$\mathcal {R}$ and precision$\mathcal {P}.$ Here, recall refers to the fraction of known positive samples that are correctly predicted by the model. Precision is defined as the fraction samples that are predicted to positive that are truly positive. Note that the F-measure does not depend on the number of correctly predicted negative samples. This is desirable, as the samples used in this evaluation are also very imbalanced. Even the largest symmetry sets in the data set only consist of 720 rotations, whereas we use a much larger set of negative samples, see below.

5.4 Generating samples

For every image I, a set of sample rotations is required that covers both the positive and negative class. Finding positive samples that lie inside the symmetry set S(I) is simple. Note that the full (discretized) symmetry set is available for every image in our annotated version of the SYMSOL data set. All elements of these annotated symmetry sets can be used directly as positive samples for evaluation.

However, negative samples cannot be deduced directly from the annotated data. But, since our classification model (and data set) are restricted to objects with discrete symmetries or single-axis continuous symmetries (Sect. 4.3.3), we can assume that all images have symmetry sets with zero volume. Consequently, any rotation sampled uniformly from SO(3) will fall outside the symmetry set with probability 1, and will therefore be a negative sample. With this knowledge, an arbitrary number of negative samples can be generated for every image.

However, for the sake of reproducibility of our evaluation results, it would be desirable to use a deterministic set of samples, rather than a random one. Moreover, the local density of randomly-generated samples inevitably varies across the rotation manifold. Therefore, a peak in the output of the network can coincide with a different number of samples, depending on this random local density. Consequently, two equally-sized peaks may incur a significantly different penalty. For these reasons, rather than generating a random set of samples, we instead follow Murphy et al. [19] and adopt a technique for generating equivolumetric grids on SO(3) developed by Yershova et al. [21]. This technique generates a deterministic grid of rotations on SO(3), such that all grid cells have the same volume. Moreover, the grid can be generated at multiple hierarchical levels, each level containing exponentially more points. In this evaluation, we use the fourth hierarchical level, which is composed of 294 thousand rotations. Therefore, there are many times fewer positive samples than negative samples. This grid will be referred to by the symbol $\mathcal {G}$ in the rest of this section.

Note that the rotations in $\mathcal {G}$ are not distributed uniformly. In contrast, they are placed deterministically, and in a regular pattern with uniform density on SO(3). Nevertheless, for the rotations in $\mathcal {G}$ to be considered proper negative samples, they must fall outside the symmetry set of every image. Since the images in the SYMSOL dataset were generated using rotations that are themselves uniformly sampled, the relative orientation of $\mathcal {G}$ with respect to any such rotation is also random. In turn, the probability of the symmetry set of any image aligning with $\mathcal {G}$ is still zero. Hence, all rotations in $\mathcal {G}$ are still guaranteed to be proper negative samples, as they fall inside any symmetry set from SYMSOL with probability zero.

Finally, to see how precision $\mathcal {P}$ relates to the classification of symmetry sets, see Fig. 8. For a given image I, the classifier predicts certain regions of SO(3) as either positive or negative, with the decision boundary depending on the threshold $\mathcal {T}$. Samples from $\mathcal {G}$ that fall inside the decision boundary are predicted as false positives. Intuitively, the tighter the decision boundary fits around the symmetry set, the fewer false positives will be predicted, and the higher the precision $\mathcal {P}$ will be.

Fig. 8

An illustration showing how the decision boundary relates to precision for both discrete (a) and continuous (b) symmetries. The enclosed blue area represents the region of SO(3) predicted as positive. Green squares represent samples from S(I) that are predicted positive. In (b) the green line represents the true continuous symmetry set. Circles represent the grid $\mathcal {G}$, where gray circles are true negative predictions and red circles are false positive predictions

5.5 Implementation details

The binary classification models were implemented in PyTorch,² according to the network design outlined in Sect. 4.3.2. The 18-layer version of ResNet was used as the first stage of the network, which is the smallest available size. Given that the images in the SYMSOL dataset show objects in a simplistic synthetic setting, this size is sufficient to achieve good performance. The red, green, and blue channels of images are normalized using mean 0.485, 0.456, and 0.406 and standard deviation 0.229, 0.224, and 0.225 respectively before being input to the ResNet model, with the purpose of being compatible with pre-trained versions of ResNet available in PyTorch.³ Finally, the output of the ResNet model is converted to the embedding by a fully connected layer with ReLU activation, where the embedding size E was fixed at 256.

The second stage MLP network was implemented with two hidden layers, each with 256 neurons and ReLU activations. The output layer consists of a single neuron with logistic sigmoid activation, which forces the output to lie in the range [0, 1].

All networks were trained for a total of 30 epochs. Training for additional epochs was not found to significantly improve convergence. The batch size was set at 32, with larger batch sizes being found to result in worse F-measure scores. Network parameters were optimized using the ADAM optimizer. The learning rate starts at $1e^{-3}$, and is lowered to $1e^{-4}$ after epoch 15, and then to $1e^{-5}$ after epoch 25.

Finally, it was found to be beneficial to freeze the parameters of the ResNet model, as well as the layer connecting it to the embedding, at the start of training. At this point, the weights of the second stage MLP are still set to their randomly-initialized values. When using a pre-trained MHP network in the first stage (Fig. 6), its weights are already meaningful. Therefore, the idea is to first let the second stage converge while keeping the first stage constant. After some time, the weights of the first stage are unfrozen, and the network is trained end-to-end. Here, we choose to unfreeze after the $4^{th}$ epoch.

5.6 Results

The evaluation of the proposed binary classification model is separated into two different experiments. The first one is an ablation study, in which we motivate the use of a positional encoding described in Sect. 4.3.2, as well as the use of a pre-trained MHP model in the first stage (Sect. 4.3.3). The second experiment studies how the performance of the final model is influenced by the number of samples K used during training.

5.6.1 Ablation

The goal of this ablation study is to test whether pre-training of the first stage and the addition of a positional encoding actually increase performance. To this end, we train the proposed model in various configurations.

As a baseline, we use a model with both positional encoding and pre-trained weights from an MHP model in the first stage. This baseline is compared against two other models, that each change one component with respect to the baseline. The first uses no positional encoding. The second one uses no MHP pre-training, but instead, it uses the default weights for ResNet-18 pre-trained on the ImangeNet classification data set. All models are trained with $K=256$ samples during training. F-measure scores for all models are shown in Table 1

Table 1 Mean F-measure scores for different ablations of the binary classification model

The baseline model consistently shows good performance with respect to the other models, achieving top scores for all but the icosahedron and cone. In general, differences in scores are largest on objects with discrete symmetries.

5.6.2 Positional encoding

Observations regarding the positional encoding mostly agree with those of Murphy et al. [19]. For objects with continuous symmetries, specifically the cone and cylinder from SYMSOL I, the positional encoding has an almost negligible impact on performance. On the cone object, performance even slightly improves over the baseline model. However, whereas Murphy et al. observed a slight decrease in performance on all objects with continuous symmetries, our data does not support this conclusion in a general sense.

In contrast, for object with discrete symmetries, the benefits are evident. Models for the tetrahedron, as well as the icosahedron from SYMSOL I, failed to train at all without the positional encoding. More specifically, they fail to converge to a meaningful solution, getting stuck outputting 0 for all inputs. Convergence for the cube and marked tetrahedron did not get stuck in the same way, but performance was significantly worse than that of the baseline. Figure 9 shows how the model without positional encoding is unable to produce a tight decision boundary around the symmetry set, in contrast to the baseline.

Fig. 9

$\pi$-Ball plots showing the difference between using positional encoding (PE) and not using it. Classifiers are evaluated on images from the marked tetrahedron data set from SYMSOL II. For each classifier, only positive predictions are shown

5.6.3 Pre-training

Similar to the use of positional encoding, differences in performance between various types of pre-training mostly show up for discrete symmetries. Unlike the models without positional encoding, all models with no MHP pre-training achieve F-measure scores that lie reasonably close to the baseline. However, for several such models, the training process had to be altered for the networks to train at all. Similar to the configuration without positional encoding, these networks got stuck outputting 0 for all inputs. In general, training networks without MHP pre-training was found to be a delicate process. Robustness of the training process greatly improved when adding the pre-training step.

5.6.4 Training sample sizes

Another important variable in the training process is the number of samples K used during training. To re-iterate, for a given image-pose pair (I, R), the loss used to train the network $f_{\theta }$ is given by Eq. (14), where K specifies the number of randomly sampled rotations used as negative samples. The higher K, the more densely these negative samples cover SO(3). To study the impact of K on performance, we train the baseline model from the previous section with different values of K on the SYMSOL II data set. Specifically, the values 64, 128, 256, 512, and 1024 are used. Figure 10 shows how the mean F-measure changes.

Fig. 10

Plots of mean F-measure and mean precision scores for the baseline model over the sample size K used during training. Results are shown for the SYMSOL II data set, where tetX and cylO refer to the marked tetrahedron and marked cylinder respectively. A threshold of $\mathcal {T}=0.8$ is used for all models

The plots show how increasing the sample size significantly improves F-measure scores. These improved scores can be attributed mostly to increases in precision, see Fig. 10b. Recall stays mostly the same, with a marginal decrease for higher values of K. Between the marked cylinder and marked tetrahedron, the latter enjoys the largest increase in scores. This is consistent with earlier results, where objects with discrete symmetries were found to be challenging for the classifier to deal with.

Deeper investigation gives an explanation for improved scores on the marked tetrahedron. In order to precisely classify its discrete symmetries, the network must produce very sharp peaks in its output. This way, the decision boundary fits tightly around the individual symmetries, thus increasing precision. With a denser sampling of rotations during training, it becomes more likely for these samples to appear in close proximity to the symmetries of the tetrahedron. Consequently, the network is incentivized to tighten its decision boundary around these symmetries, as to correctly distinguish them from the random negative samples during training. Therefore, it is intuitive that precision increases for higher values of K.

Figure 11 illustrates this effect, by zooming in on one of the peaks generated in the output of the network. A one-dimensional slice of rotations is taken along the object-local x-axis, and the output of the network is computed at each rotation. These plots give a clear example of how larger values of K result in sharper output peaks, thus increasing precision.

Fig. 11

Plots zooming in on a single output peak produced by various binary classification models on an image of the marked tetrahedron. Each model is trained with a different number of training samples K. The output is shown over a one-dimensional slice of rotations taken along the object local x-axis, centered on the ground truth rotation. Relative angles on the x-axis are shown in radians

5.6.5 Summary

The proposed binary classification network is able to faithfully reconstruct symmetry sets for images of the SYMSOL data set. This is true for both the simplistic symmetry sets created by globally symmetric objects, as well as more complicated sets created by nearly symmetric objects.

An ablation study shows how the addition of a positional encoding, as well as a pre-trained first stage, help increase (i) the robustness of the training process and (ii) the F-measure scores of the model. The positional encoding is found to be particularly influential, allowing networks to produce tight decision boundaries around discrete symmetric rotations.

Increasing the sample size parameter K during training is shown to further increase precision. Increasing the number K incentivizes the network to produce sharper peaks in its output. The benefits of this are most significant for discrete symmetries, where the decision boundary is preferably as tight as possible. In practise, retrieving the entire symmetry set is, however, not feasible, since it may contain a huge number of poses. Nevertheless, the proposed binary classification model represents an improvement with respect to the small number of discrete hypotheses provided by an MHP model. Although the model is more expressive than an MHP one, it can compute an arbitrary number of hypotheses. In theory, with an infinite number of diverse hypotheses, the full symmetry set could be reconstructed. In practise, a number can be taken according to computational constraints, or use-case specific needs. Another option is to adaptively sample the rotation manifold, i.e., increase the number of samples in the promixity of the (discrete) symmetries of an object and decrease it far away.

6 Conclusion

In this paper we addressed the issues posed by rotational symmetries in orientation estimation. Existing literature in pose estimation either uses manual canonicalization of symmetric poses, or symmetry-aware loss functions based on object CAD models, to predict a single correct pose. Other work treats ambiguity as a cause of uncertainty, predicting distributions over poses. The former approach gives no information on the set of possibly correct poses under ambiguity, called the symmetry set, and does not scale to symmetries induced by occlusions. The latter often requires parameterization and computationally expensive normalization to obtain a complex distribution on SO(3).

Ground truth symmetry set annotations for every image are required to evaluate orientation estimation algorithms on symmetric objects and nearly-symmetric objects. To this end, we have introduced a data set with annotated symmetry sets covering nearly-symmetric objects under self-occlusion. This data set is based on the SYMSOL II data set introduced in earlier work. Known patterns in the symmetries are exploited to generate candidate rotations for the symmetry set of every image.

In this work, we we model orientation estimation as a binary classification problem on the combined space of images and SO(3). Our solution is based on existing work in implicit shape reconstruction and pose distribution estimation, but requires a restriction to only discrete and single-axis symmetries. The resulting network is able to learn accurate decision boundaries, separating symmetry sets from the rest of SO(3) at continuous resolution. Quantitative metrics show the performance of the model on our annotated data set, and confirm the benefit of design choices in an ablation study.

Regarding limitations, our method requires ground truth symmetry set annotations which are not readily available. Furthermore, our method only considers orientation and does not handle translation. Finally, generating negative samples for training our model, in particular for objects with discrete symmetries, is relatively expensive if accurate reconstructions of symmetry sets are required; also the inference time is negatively affected in this situation.

6.1 Future work

Future research could apply the method to object tracking or extend to a multi-view framework. In both cases, information from multiple view points can be combined by intersecting, or otherwise combining, the symmetry sets predicted from different images.

Though our binary classification model shows good performance on the simplistic SYMSOL data set, further research is required into its robustness when objects appear in more complex synthetic environments, and ultimately, in real images. To this end, our methodology of using rendered segmentation maps to compute symmetry set annotations can be further exploited. We believe that the same methodology can be applied to objects in much more complicated environments, like the synthetic images used in the BOP challenge [2].

Finally, the proposed training strategy only works when symmetry sets have zero volume. More analysis is required to define a category of objects that can satisfy this requirement when considering occlusion-induced symmetries.