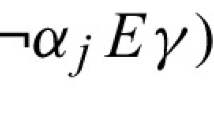Skip to main content
Springer Nature Link
Log in

On vectorizations of unary generalized quantifiers

  • Published:
Archive for Mathematical Logic Aims and scope Submit manuscript

Abstract

Vectorization of a class of structures is a natural notion in finite model theory. Roughly speaking, vectorizations allow tuples to be treated similarly to elements of structures. The importance of vectorizations is highlighted by the fact that if the complexity class PTIME corresponds to a logic with reasonable syntax, then it corresponds to a logic generated via vectorizations by a single generalized quantifier (Dawar in J Log Comput 5(2):213–226, 1995). It is somewhat surprising, then, that there have been few systematic studies of the expressive power of vectorizations of various quantifiers. In the present paper, we consider the simplest case: the cardinality quantifiers C S . We show that, in general, the expressive power of the vectorized quantifier logic \({{\rm FO}(\{{\mathsf C}_S^{(n)}\, | \, n \in \mathbb{Z}_+\})}\) is much greater than the expressive power of the non-vectorized logic FO(C S ).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Dawar A.: Generalized quantifiers and logical reducibilities. J. Log. Comput. 5(2), 213–226 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ebbinghaus, H.D.: Extended logics: the general framework. In: Model-Theoretic Logics, Perspect. Math. Logic, pp. 25–76. Springer, New York (1985)

  3. Graham R.L., Rothschild B.L., Spencer J.H.: Ramsey Theory. 2nd edn. Wiley-Interscience Series in Discrete Mathematics and Optimization. Wiley, New York (1990) (A Wiley-Interscience Publication)

    Google Scholar 

  4. Gurevich, Y.: Toward logic tailored for computational complexity. In: Computation and Proof Theory (Aachen, 1983), Lecture Notes in Math., vol. 1104, pp. 175–216. Springer, Berlin (1984). doi:10.1007/BFb0099486. http://dx.doi.org/10.1007/BFb0099486

  5. Gurevich, Y.: Logic and the challenge of computer science. In: Trends in Theoretical Computer Science (Udine, 1984), Principles Comput. Sci. Ser., vol. 12, pp. 1–57. Computer Sci. Press, Rockville, MD (1988)

  6. Hella L.: Definability hierarchies of generalized quantifiers. Ann. Pure Appl. Log. 43(3), 235–271 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  7. Hella L., Krynicki M.: Remarks on the Cartesian closure. Z. Math. Logik Grundlag. Math. 37(6), 539–545 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hella, L., Luosto, K.: Finite generation problem and n-ary quantifiers. In: Krynicki, M., Mostowski, M., Szczerba, L.W. (eds.) Quantifiers: Logics, Models and Computation, vol. I, pp. 63–104. Kluwer (1995)

  9. Hella L., Nurmonen J.: Vectorization hierarchies of some graph quantifiers. Arch. Math. Log. 39(3), 183–207 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kaila R.: On probabilistic elimination of generalized quantifiers. Random Struct. Algorithms 19(1), 1–36 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  11. Kolaitis, P.G.: Implicit definability on finite structures and unambiguous computations. In: Fifth Annual IEEE Symposium on Logic in Computer Science (Philadelphia, PA, 1990), pp. 168–180. IEEE Comput. Soc. Press, Los Alamitos, CA (1990)

  12. Kolaitis P.G., Väänänen J.A.: Generalized quantifiers and pebble games on finite structures. Ann. Pure Appl. Log. 74(1), 23–75 (1995)

    Article  MATH  Google Scholar 

  13. Krynicki M.: Notion of interpretation and nonelementary languages. Z. Math. Logik Grundlag. Math. 34(6), 541–552 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lindström P.: First order predicate logic with generalized quantifiers. Theoria 32, 186–195 (1966)

    MathSciNet  MATH  Google Scholar 

  15. Lothaire M.: Combinatorics on Words, Encyclopedia of Mathematics and its Applications, vol. 17. Addison-Wesley, Reading, Mass (1983)

    Google Scholar 

  16. Lothaire M.: Algebraic Combinatorics on Words, Encyclopedia of Mathematics and its Applications, vol. 90. Cambridge University Press, Cambridge (2002)

    Google Scholar 

  17. Luosto K.: Hierarchies of monadic generalized quantifiers. J. Symb. Log. 65(3), 1241–1263 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  18. Makowsky J.A., Shelah S., Stavi J.: Δ-logics and generalized quantifiers. Ann. Math. Log. 10(2), 155–192 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  19. Nešetřil J., Väänänen J.A.: Combinatorics and quantifiers. Comment. Math. Univ. Carolin. 37(3), 433–443 (1996)

    MathSciNet  MATH  Google Scholar 

  20. Väänänen, J.: A hierarchy theorem for Lindström quantifiers. In: Furberg, T.W.M., Åberg, C. (eds.) Logic and Abstraction, vol. Acta Philosophica Gothoburgesia 1, pp. 317–323 (1986)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, University of Helsinki, PL 68 (Gustaf Hällströmin katu 2b), 00014, Helsinki, Finland

    Kerkko Luosto

Authors
  1. Kerkko Luosto
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Kerkko Luosto.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luosto, K. On vectorizations of unary generalized quantifiers. Arch. Math. Logic 51, 241–255 (2012). https://doi.org/10.1007/s00153-011-0262-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00153-011-0262-7

Keywords

Mathematics Subject Classification (2000)