Abstract
We study Basic Arithmetic, \(\textsf{BA}\) introduced by Ruitenburg (Notre Dame J Formal Logic 39:18–46, 1998). \(\textsf{BA}\) is an arithmetical theory based on basic logic which is weaker than intuitionistic logic. We show that the class of the provably total recursive functions of \(\textsf{BA}\) is a proper sub-class of the primitive recursive functions. Three extensions of \(\textsf{BA}\), called \(\textsf{BA}+\mathsf U\), \(\mathsf {BA_{\mathrm c}}\) and \(\textsf{EBA}\) are investigated with relation to their provably total recursive functions. It is shown that the provably total recursive functions of these three extensions of \(\textsf{BA}\) are exactly the primitive recursive functions. Moreover, among other things, it is shown that the well-known MRDP theorem does not hold in \(\textsf{BA}\), \(\textsf{BA}+\mathsf U\), \(\mathsf {BA_{\mathrm c}}\), but holds in \(\textsf{EBA}\).
Similar content being viewed by others
Notes
In the literature, the term “geometric logic" is usually used for a logic with infinitary disjunction, and the formulas with only finitary disjunction are called coherent geometric formulas. In this paper, we only work with finitary languages, and only nullary and binary disjunction (\(\bot \) and \(\vee \), respectively) are included in the language, which are sufficient for making up all the finitary disjunctions. Also, derivability in geometric logic is often considered in a context of a finite sequence of variables, which for example allows for an empty domain of discourse when considering semantics. We will use the term “geometric" only for reference to the finitary part of the language and logic, and consider derivability without variable contexts.
This notation “\({{\,\textrm{Th}\,}}\)" is different from that used in [12], which is for sequents and not just sentences.
Every \(\exists _1^+\) formula is geometric, and every gemetric formula is equivalent to a \(\exists _1^+\) formula over geometric logic, which is the weakest logic we are considering. We could simply skip this definition, and work only with geometric formulas instead. Our purpose of the definition is only to use the notation that already has been used in the literature.
The reader interested in the main results of the next Sections may safely skip this Subsection, with the exception that the formula \({\textbf {A}} _{\mathrm c}\) first introduced in Proposition 3.24 will appear repeatedly later on.
We can take \(C(x,y,z)\equiv 2z=(x+y)\cdot S(x+y)+2y\), and then formalize the usual arguments for the desired properties of the Cantor pairing function (totality, uniqueness and bijectivity) inside \({\mathsf I}\mathsf \Sigma _1\).
The program of a partial recursive function shows how it is defined in terms of zero successor and projection functions by repeatedly applying composition, primitive recursion and minimization. Note that by choosing a suitable coding, we can assume that every natural number is the code of a program.
It is true that \({\mathbb {N}}\models {\textbf {PR}} (n)\) implies \(\varphi _n\in \varvec{\mathcal{P}\mathcal{R}}\), but not vice versa. However, for every primitive recursive function f there is a natural number n such that \(\varphi _n=f\) and \({\mathbb {N}}\models {\textbf {PR}} (n)\).
Note the slight difference between the current definition and the usual negative translation, in which \(A^{\mathrm g}=\lnot \lnot A\) for atomic A.
References
Ardeshir, M., Hesaam, B.: An introduction to basic arithmetic. Logic J. IGPL 16, 1–13 (2008)
Ardeshir, M., Khaniki, E., Shahriari, M.: A counter-example to polynomially bounded realizability of Basic Arithmetic. Notre Dame J. Formal Logic 60, 481–489 (2019)
Buss, S.R.: Intuitionistic validity in T-normal Kripke structures. Ann. Pure Appl. Logic 59, 159–173 (1993)
Buss, S.R.: An Introduction to Proof Theory. In: Buss, S.R. (ed.) Handbook of Proof Theory, pp. 1–78. Elsevier, Amsterdam (1998)
Gaifman, H., Dimitracopoulos, C.: Fragments of arithmetic and the MRDP theorem. In: Logic and Algorithmic, Monographie 30 de L’Enseignement Mathematique, pp. 187–206
Ghasemloo, K.: The provably total functions of \({{\sf I}}\exists ^{+}\) (in Persian), MSc. thesis, Department of Mathematical Sciences, Sharif University of Thechnology (2008)
Hajek, P., Pudlak, P.: Metamathematics of First-Order Arithmetic. Springer, Berlin (1998). (2nd printing)
Kaye, R.: Diophantine Induction. Ann. Pure Appl. Logic 46(1), 1–40 (1990)
Kaye, R.: Models of Peano Arithmetic. Oxford University Press, New York (1991)
Ruitenburg, W.: Constructive logic and the paradoxes. Modern Logic 1, 271–301 (1991)
Ruitenburg, W.: Basic Logic and Fregean Set Theory. In: Barendregt, H.P., Bezem, M., Klop, J.W. (eds.) Dirk van Dalen Festschrift, Quaestiones infinitae. Utrecht University, vol. 5, pp. 121–142. Department of Philosophy, Utrecht (1993)
Ruitenburg, W.: Basic predicate calculus. Notre Dame J. Formal Logic 39, 18–46 (1998)
Salehi, S.: Provably total functions of basic arithmetic. Math. Logic Quart. 49(3), 316–322 (2003)
Salehi, S.: Polynomially bounded recursive realizability. Notre Dame J. Formal Logic 46, 407–417 (2005)
Takeuti, G.: Proof Theory, 2nd edn. Elsevier, New York (1987)
van Dalen, D.: Logic and Structure. Springer, Berlin Heidelberg (2008)
Vickers, S.: Locales and toposes as spaces. In: Aiello, M., Pratt-Hartmann, I., van Benthem, J. (eds.) Handbook of Spatial Logics, pp. 429–496. Springer, Dordrecht (2007)
Wehmeier, K.F.: Classical and intuitionistic models of arithmetic. Notre Dame J. Formal Logic 37, 452–461 (1996)
Wehmeier, K.F.: Fragments of HA based on \(\Sigma _ 1\)-induction. Arch. Math. Logic 37, 37–49 (1997)
Acknowledgements
We thank S. M. Mojtahedi for his helpful comments in our discussions, E. Jeřábek for answering our questions about models of weak theories of arithmetic and W. Ruitenberg for his comments, in particular his suggestion to us looking at the cut-off subtraction over BA.
Author information
Authors and Affiliations
Contributions
All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 The system \(\textsf{LK}\)
The system \(\textsf{LK}\) (see sections 1.2.2 and 2.3.2 of [4]) is a sequent calculus formed by the following axioms and rules: (Here, \(\Delta \), \(\Delta '\) and \(\Delta ''\) are finite lists of formulas)
1.1.1 Structural axiom

1.1.2 Structural rules

1.1.3 Logical axioms

1.1.4 Logical rules

In each rule, the formulas appearing in \(\Delta \), \(\Delta '\) or \(\Delta ''\), are called context. Other formulas which appear in the upper sequents are called active formulas, and those which appear in the lower sequents are called principal formulas. The active formula of the cut rule (Cut) is called the cut formula.
1.2 Arithmetical theories based on \(\textsf{LK}\)
Arithmetical theories over \(\textsf{LK}\) are formalized in the language of arithmetic, with the additional axioms of logic with equality (see section 2.3.3 of [4]), and axioms and rules specific to arithmetic (see section 2.4.6 of [4]):
1.2.1 Equality axioms

1.2.2 Arithmetical axioms

1.2.3 Arithmetical rule
-
 , where t is substitutable for x in A, and x is not free in \(\Delta ,\Delta '\)
, where t is substitutable for x in A, and x is not free in \(\Delta ,\Delta '\)
The formula A in the induction rule (ind) is called the induction formula. If the induction formula is restricted to a class \({\mathcal {C}}\) of formulas, the rule is called the \({\mathcal {C}}\)-induction rule.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ardeshir, M., Khaniki, E. & Shahriari, M. The provably total functions of basic arithmetic and its extensions. Arch. Math. Logic 64, 205–257 (2025). https://doi.org/10.1007/s00153-024-00939-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-024-00939-0
Keywords
- Basic logic
- Basic arithmetic
- Heyting arithmetic
- Constructive mathematics
- Provably total function
- Primitive recursive function



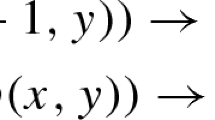
 , where t is substitutable for x in A, and x is not free in
, where t is substitutable for x in A, and x is not free in