Skip to main content
SpringerLink
Log in

Composite support vector quantile regression estimation

  • Original Paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

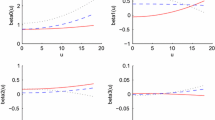
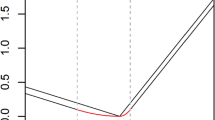
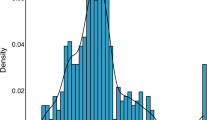
In this paper we propose a new nonparametric regression method called composite support vector quantile regression (CSVQR) that combines the formulations of support vector regression and composite quantile regression. First the CSVQR using the quadratic programming (QP) is proposed and then the CSVQR utilizing the iteratively reweighted least squares (IRWLS) procedure is proposed to overcome weakness of the QP based method in terms of computation time. The IRWLS procedure based method enables us to derive a generalized cross validation (GCV) function that is easier and faster than the conventional cross validation function. The GCV function facilitates choosing the hyperparameters that affect the performance of the CSVQR and saving computation time. Numerical experiment results are presented to illustrate the performance of the proposed method

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  • Cole T, Green P (1992) Smoothing reference centile curves: the LMS method and penalized likelihood. Stat Med 11:1305–1319

    Article  Google Scholar 

  • Craven P, Wahba G (1979) Smothing noisy data with spline functions. Numer Math 31:377–403

    Article  MATH  MathSciNet  Google Scholar 

  • Cristianini N, Shawe-Taylor J (2000) An introduction to support vector machines. Cambridge University Press, Cambridge

    Google Scholar 

  • Fan J, Gijbels I (1992) Variable bandwidth and local linear regression smoothers. Ann Stat 20:2008–2036

    Article  MATH  MathSciNet  Google Scholar 

  • Gunn S (1998) Support vector machines for classification and regression. University of Southampton, ISIS Technical Report

    Google Scholar 

  • Härdle W (1990) Applied nonparametric regression. Cambridge University Press, Cambridge

  • Heagerty P, Pepe M (1999) Semiparametric estimation of regression quantiles with application to standardizing weight for height and age in U.S. children. J R Stat Soc Ser C 48:533–551

    Article  MATH  Google Scholar 

  • Hendricks W, Koenker R (1992) Hierarchical spline models for conditional quantiles and the demand for electricity. J Am Stat Assoc 93:58–68

    Article  Google Scholar 

  • Jiang R, Zhou Z, Qian W, Shao W (2012) Single-index composite quantile regression. J Korean Stat Soc 41:323–332

    Article  MATH  Google Scholar 

  • Kai B, Li R, Zou H (2010) Local composite quantile regression smoothing: an efficient and safe alternative to local polynomial regression. J R Stat Soc Ser B 72:49–69

    Article  MathSciNet  Google Scholar 

  • Kai B, Li R, Zou H (2011) New efficient estimation and variable selection methods for semiparametric varying-coefficient partially linear models. Ann Stat 39:305–332

    Article  MATH  MathSciNet  Google Scholar 

  • Koenker R, Bassett G (1978) Regression quantiles. Econometrica 46:33–50

    Article  MATH  MathSciNet  Google Scholar 

  • Kimeldorf G, Wahba G (1971) Some results on Tchebycheffian spline functions. J Math Anal Appl 33:82–95

    Article  MATH  MathSciNet  Google Scholar 

  • Koenker R, Geling R (2001) Reappraising medfly longevity: a quantile regression survival analysis. J Am Stat Assoc 96:458–468

    Article  MATH  MathSciNet  Google Scholar 

  • Koenker R, Hallock KF (2001) Quantile regression. J Econ Perspect 15:143–156

    Article  Google Scholar 

  • Kuhn H, Tucker A (1951) Nonlinear programming. In: Proceedings of 2nd Berkeley symposium. University of California Press, Berkeley, pp 481–492

  • Li Y, Kiu Y, Zhu J (2007) Quantile regression in reproducing kernel Hilbert space. J Am Stat Assoc 103:255–268

    Article  Google Scholar 

  • Mercer J (1909) Functions of positive and negative type and their connection with theory of integral equations. Philos Trans R Soc A, 415–446

  • Powell JL (1984) Least absolute deviations estimation for the censored regression model. J Econ 25:303–325

    Article  MATH  Google Scholar 

  • Shim J, Hwang C (2009) Support vector censored quantile regression under random censoring. Comput Stat Data Anal 53:912–919

    Article  MATH  MathSciNet  Google Scholar 

  • Smola A, Schölkopf B (1998) On a kernel-based method for pattern recognition, regression, approximation and operator inversion. Algorithmica 22:211–231

    Article  MATH  MathSciNet  Google Scholar 

  • Suyekns JAK (2000) Least squares support vector machine for classification and nonlinear modelling. Neural Network World, Special Issue on PASE 2000(10):29–48

    Google Scholar 

  • Takeuchi I, Le QV, Sears TD, Smola AJ (2006) Nonparametric quantile estimation. J Mach Learn Res 7:1231–1264

    MATH  MathSciNet  Google Scholar 

  • Vapnik VN (1995) The nature of statistical learning theory. Springer, New York

    Book  MATH  Google Scholar 

  • Vapnik VN (1998) Statistical learning theory. Springer, New York

    MATH  Google Scholar 

  • Wang L (ed) (2005) Support vector machines: theory and application. Springer, Berlin, Heidelberg, New York

    Google Scholar 

  • Wei Y, He X (2006) Conditional growth charts (with discussions). Ann Stat 34:2069–2097

    Article  MATH  MathSciNet  Google Scholar 

  • Ye A, Hyndman RJ, Le Z (2006) Local linear multivariate regression with variable bandwidth in the presence of heteroscedasticity. Working paper of Department of Econometrics and Business Statistics, Monash University, Australia

  • Ying Z, Jung SH, Wei LJ (1995) Survival analysis with median regression models. J Am Stat Assoc 90:178–184

    Article  MATH  MathSciNet  Google Scholar 

  • Yuan M (2006) GACV for quantile smoothing splines. Conput Stat Data Anal 5:813–829

    Article  Google Scholar 

  • Yu K, Lu Z, Stander J (2003) Quantile regression: applications and current research area. The Statistician 52:331–350

    MathSciNet  Google Scholar 

  • Zou H, Yuan M (2008) Composite quantile regression and the oracle model selection theory. Ann Stat 36:1108–1126

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work was supported by the National Research Foundation of Korea Grant funded by the Korean Government (NRF-2012S1A3A2033330). This research was also supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology (2012000646) and (2011-0009705).

Author information

Authors and Affiliations

  1. Department of Data Science and Institute of Statistical Information, Inje University, Obang-Dong, Kimhae, 621-749, Korea

    Jooyong Shim & Kyungha Seok

  2. Department of Applied Statistics, Dankook University, Yongin, Gyeonggido, 448-701, Korea

    Changha Hwang

Authors
  1. Jooyong Shim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Changha Hwang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kyungha Seok
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kyungha Seok.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shim, J., Hwang, C. & Seok, K. Composite support vector quantile regression estimation. Comput Stat 29, 1651–1665 (2014). https://doi.org/10.1007/s00180-014-0511-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-014-0511-4

Keywords

Search

Navigation