Functional coefficient seasonal time series models with an application of Hawaii tourism data

Abstract

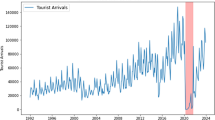
In this article, motivated by an analysis of the monthly number of tourists visiting Hawaii, we propose a new class of nonparametric seasonal time series models under the framework of the functional coefficient model. The coefficients change over time and consist of the trend and seasonal components to characterize seasonality. A local linear approach is developed to estimate the nonparametric trend and seasonal effect functions. The consistency of the proposed estimators is obtained without specifying the error distribution and the asymptotic normality of the proposed estimators is established under the $\alpha$-mixing conditions. A consistent estimator of the asymptotic variance is also provided. The proposed methodologies are illustrated by two simulated examples and the model is applied to characterizing the seasonality of the monthly number of tourists visiting Hawaii.

Appendix: Mathematical proofs

We first list all the assumptions needed for the asymptotic theory in Sect. 2.2 although some of them might not be the weakest possible. Note that the same notations in Sect. 2 are used here. Throughout this appendix, we denote by $C$ a generic constant, which may take different values at different appearances.

Assumption A

• A1. The kernel $K(u)$ is symmetric and satisfies the Lipschitz condition and $u\,K(u)$ is bounded.

• A2. For each $n$, $\{(\mathcal{X}_{t},\,\mathbf{e}_{nt})\}_{t=1}^n$ have the same joint distribution as $\{(\mathcal{X}_{t},\;\varvec{\xi }_t)\}_{t=1}^n$, where the time series $\{(\mathcal{X}_{t},\;\varvec{\xi }_t)\}$ is strictly stationary $\alpha$-mixing. Assume that there exists $\delta >0$ such that $E|\varvec{\xi }_t|^{2(1+ \delta )}<\infty$, $E|\mathcal{X}_{t}|^{4(1+\delta )}<\infty$, and the mixing coefficient $\alpha (n)=O\left( n^{-(2+\delta )(1+\delta )/\delta }\right)$.

• A3. $n\,h^{1+4/\delta }\rightarrow \infty$.

Remark 10

Let $r_{jm}(k)$ denote the $(j,m)$-th element of $\mathbf{R}(k)$. By the Davydov’s inequality (see, e.g., Corollary A.2 in Hall and Heyde 1980), Assumption A2 implies that $|r_{jm}(k)|\le C\,\alpha ^{\delta /(2+\delta )}(k)$ so that $\sum _{k=-\infty }^\infty |r_{jm}(k)|<\infty$.

Lemma A1

Under the assumptions of Theorem 1, we have

$$\begin{aligned} \hbox {Var}({\mathbf {P}}_{n0})=\nu _0\,\varvec{\Sigma }_0+o(1)\quad \text{ and }\quad \mathbf{P}_{n1}=o_p(1), \end{aligned}$$

where, for $k=0, 1$,

$$\begin{aligned} {\mathbf {P}}_{nk}=h^{1/2}\; n^{-1/2}\;\sum _{t=1}^n (s_t-s)^k\;\mathbf{e}_{nt}^*\,K_h(s_t-s) \end{aligned}$$

with $\mathbf{e}_{nt}^*=\mathcal{X}_t^T\,\mathbf{e}_{nt}$.

Proof

By the stationarity of $\{\varvec{\xi }_j\}$ and $\mathcal{X}_t$,

$$\begin{aligned} \text{ var }(\mathbf{P}_{n0})= & {} n^{-1}\,h\,\sum _{1\le k,\, l\le n}\mathbf{R}(k-l)\,K_h(s_k-s)\,K_h(s_l-s)\\= & {} n^{-1}\,h\,\mathbf{R}(0)\,\sum _{k=1}^n K_h^2(s_k-s)\\&+ 2\,n^{-1}\,h\,\sum _{1\le l<k\le n}\mathbf{R}(k-l)\,K_h(s_k-s)\,K_h(s_l-s) \\\equiv & {} \mathbf{I}_1+\mathbf{I}_2. \end{aligned}$$

Clearly, by the Riemann sum approximation of an integral,

$$\begin{aligned} \mathbf{I}_1\approx \mathbf{R}(0)\;h\,\int _0^1 K_h^2(u-s)du\approx \nu _0\,\mathbf{R}(0). \end{aligned}$$

Since $n\,h\rightarrow \infty$, there exists $c_n\rightarrow \infty$ such that $c_n/(n\,h)\rightarrow 0$. Let $S_1=\{(k,l): 1\le k-l\le c_n;\, 1\le l<k\le n\}$ and $S_2=\{(k,l):\,1\le l<k\le n\} {\setminus } S_1$. Then, $\mathbf{I}_2$ is split into two terms as $\sum _{S_1}(\cdots )$, denoted by $\mathbf{I}_{21}$, and $\sum _{S_2}(\cdots )$, denoted by $\mathbf{I}_{22}$. Since $K(\cdot )$ is bounded, then, $K_h(\cdot )\le C/h$ and $n^{-1}\sum _{k=1}^nK_h(t_k-t)\le C$. In conjunction with the Davydov’s inequality (see, e.g., Corollary A.2 in Hall and Heyde 1980), we have, for the $(j,m)$-th element of $\mathbf{I}_{22}$,

$$\begin{aligned} |\mathbf{I}_{22(jm)}|\le & {} 2n^{-1}h \;\sum _{S_2}\,|r_{jm}(k-l)|\,K_h(s_k-s)\,K_h(s_l-s)\\\le & {} C\;n^{-1}\,h\,\sum _{S_2} \alpha ^{\delta /(2+\delta )}(k-l)K_h(s_k-s)\,K_h(s_l-s)\\\le & {} C\, n^{-1}\,\sum _{k=1}^n K_h(s_k-s)\sum _{k_1>c_n}\alpha ^{\delta /(2+\delta )}(k_1)\\\le & {} C\;\sum _{k_1>c_n}\alpha ^{\delta /(2+\delta )}(k_1) \\\le & {} C\,c_n^{-\delta }\rightarrow 0 \end{aligned}$$

by Assumption A2 and the fact that $c_n\rightarrow \infty$. For any $(k,l)\in S_1$, by Assumption A1

$$\begin{aligned} |K_h(s_k-s)-K_h(s_l-s)|\le C\,h^{-1}\,(s_k-s_l)/h\le C\,c_n/(n\,h^2), \end{aligned}$$

which implies that

$$\begin{aligned} |\mathbf{I}_{212(jm)}|\equiv & {} \left| 2\,n^{-1}\,h\,\sum _{l=1}^{n-1}\sum _{1\le k-l\le c_n}r_{jm}(k-l)\,\{K_h(s_k-s)-K_h(s_l-s)\}\,K_h(s_l-s)\right| \\\le & {} C\,c_n\,n^{-2}\,h^{-1}\,\sum _{l=1}^{n-1}\sum _{1\le k-l\le c_n}|r_{jm}(k-l)|\,K_h(s_l-s)\\\le & {} C \, c_n\,n^{-2}\,h^{-1}\,\sum _{l=1}^{n-1}K_h(s_l-s)\;\sum _{k\ge 1}|r_{jm}(k)| \\\le & {} C\,c_n/(n\,h)\rightarrow 0 \end{aligned}$$

by Remark 10 and the fact that $c_n/(n\,h)\rightarrow 0$. Therefore,

$$\begin{aligned} \mathbf{I}_{21(jm)}= & {} 2\,n^{-1}\,h\,\sum _{l=1}^{n-1}\sum _{1\le k-l\le c_n}r_{jm}(k-l)\,K_h(s_k-s)\,K_h(s_l-s)\\= & {} 2\,n^{-1}\,h\,\sum _{l=1}^{n-1}K_h^2(s_l-s)\sum _{1\le k-l\le c_n}r_{jm}(k-l)+\mathbf{I}_{212(jm)} \\\rightarrow & {} 2\,\nu _0\,\sum _{k=1}^\infty r_{jm}(k). \end{aligned}$$

Thus,

$$\begin{aligned} \text{ var }(\mathbf{P}_{n0})\rightarrow \nu _0\,\left( \mathbf{R}(0)+2\,\sum _{k=1}^\infty \mathbf{R}(k)\right) =\nu _0\,\varvec{\Sigma }_0. \end{aligned}$$

On the other hand, by Assumption A1, we have

$$\begin{aligned} \text{ var }(\mathbf{P}_{n1})= & {} n^{-1}\,h\,\sum _{1\le k,\, l\le n}\mathbf{R}(k-l)\,(s_k-s)(s_l-s)K_h(s_k-s)\,K_h(s_l-s)\\\le & {} C\; n^{-1}\,h\,\sum _{1\le k,\,l\le n} |\mathbf{R}(k-l)| \\\le & {} C\;h\;\sum _{k=-\infty }^\infty |\mathbf{R}(k)|\rightarrow \mathbf{0}. \end{aligned}$$

This proves the lemma. $\square$

Proof of Theorem 1

Similar to the proof used in Lemma A1, we have

$$\begin{aligned} h^{-k}\,\mathbf{G}_k(s)=\mu _k\,\mathbf{G}+o_p(1), \end{aligned}$$

(14)

where $\mathbf{G}_k$ for $k\ge 0$ is defined in (9), so that

$$\begin{aligned} \begin{pmatrix} \mathbf{G}_0 &{}\quad \mathbf{G}_1/h\\ \mathbf{G}_1/h &{}\quad \mathbf{G}_2/h^2\\ \end{pmatrix} =\text{ diag }\{\mathbf{G}, \mu _2\,\mathbf{G}\}+o_p(1). \end{aligned}$$

We re-write $\mathbf{M}_k$ as

$$\begin{aligned} \mathbf{M}_k=\mathbf{M}_k^*+(nh)^{-1/2}\mathbf{P}_{nk}, \end{aligned}$$

where $\mathbf{M}_k$ is defined in (9), $\mathbf{P}_{nk}$ is defined in Lemma A1, and $\mathbf{M}_k^*=n^{-1}\,\sum _{t=1}^n (s_t-s)^k\,\mathcal{X}_t^T\varvec{\theta }(s_t)\,K_h(s_t-s)$. By a Taylor expansion, for any $k\ge 0$ and $s_t$ in a neighborhood of $s$,

$$\begin{aligned} \mathbf{M}_k^*=\mathbf{G}_{k}\,\varvec{\theta }(s)+\mathbf{G}_{k+1}\,\varvec{\theta }'(s)+{1\over 2}\,\mathbf{G}_{k+2}\,\varvec{\theta }''(s)+o_p(h^2), \end{aligned}$$

so that by (9),

$$\begin{aligned}&\begin{pmatrix}\widehat{\varvec{\theta }}_0\\ \widehat{\varvec{\theta }}'_1 \end{pmatrix}-\begin{pmatrix}{\varvec{\theta }}_0\\ {\varvec{\theta }}'_1 \end{pmatrix}\\&\quad ={1\over 2}\,\begin{pmatrix}\mathbf{G}_0 &{}\quad \mathbf{G}_1\\ \mathbf{G}_1 &{}\quad \mathbf{G}_2 \end{pmatrix}^{-1}\;\begin{pmatrix}\mathbf{G}_2\\ \mathbf{G}_3 \end{pmatrix}\,\varvec{\theta }''(s)+o_p(h^2) +(nh)^{-1}\begin{pmatrix}\mathbf{G}_0 &{}\quad \mathbf{G}_1\\ \mathbf{G}_1 &{}\quad \mathbf{G}_2\end{pmatrix}^{-1}\;\begin{pmatrix}\mathbf{P}_{n0}\\ \mathbf{P}_{n1}\end{pmatrix}, \end{aligned}$$

which implies that

$$\begin{aligned} \sqrt{n\,h}\;\left\{ \widehat{\varvec{\theta }}(s)-\varvec{\theta }(s)-{h^2\over 2}\,\mu _2\,\varvec{\theta }''(s)+o(h^2) \right\} =\mathbf{G}^{-1}\,\mathbf{P}_{n0}+o_p(1). \end{aligned}$$

(15)

Therefore, it follows from (15) that the term ${1\over 2}\,h^2\,\mu _2\,\varvec{\theta }''(t)$ on the right hand side of (15) serves as the asymptotic bias, and that to establish the asymptotic normality of $\widehat{\varvec{\theta }}(s)$, one only needs to establish the asymptotic normality for $\mathbf{P}_{n0}$ . To this end, the Cramér-Wold device is used. For any unit vector $\mathbf{d}\in \mathfrak {R}^d$, let $Z_{n,t}=n^{-1/2}\;h^{1/2}\;\mathbf{d}^T\;\mathbf{e}_{nt}\,K_h(s_t-s)$. Then, $\mathbf{d}^T\,\mathbf{P}_{n0}=\sum _{t=1}^nZ_{n,t}$ and by Lemma A1,

$$\begin{aligned} \text{ var }\left( \mathbf{d}^T\,\mathbf{P}_{n0}\right) =\nu _0\,\mathbf{d}^T\,\varvec{\Sigma }_0\,\mathbf{d}\;\{1+o(1)\}\equiv \theta ^2_d\; \{1+o(1)\}. \end{aligned}$$

(16)

Now, the Doob’s small-block and large-block technique is used. Namely, partition $\{1,\,\ldots , \,n\}$ into $2\,q_n+1$ subsets with large-block of size $r_n=\left\lfloor (n\,h)^{1/2}\right\rfloor$ and small-block of size $s_n=\left\lfloor (n\,h)^{1/2}/\log n\right\rfloor$, where $q_n=\left\lfloor {n\over r_n+s_n}\right\rfloor$. Then, $q_n\,\alpha (s_n)\le C\;n^{-(\tau -1)/2} \,h^{-(\tau +1)/2}\,\log ^\tau n$, where $\tau =(2+\delta )(1+\delta )/\delta$, and $q_n\,\alpha (s_n)\rightarrow 0$ by Assumption A3. Let $r_j^*=j\,(r_n+s_n)$ and define the random variables, for $0\le j\le q_n-1$,

$$\begin{aligned} \eta _j=\sum _{t=r_j^*+1}^{r_j^*+r_n}Z_{n,t},\quad \zeta _j=\sum _{t=r_j^*+r_n+1} ^{r_{j+1}^*}Z_{n,t},\quad \mathrm{and}\quad \mathbf{Q}_{n,3}=\sum _{t=r_{q_n}^*+1}^n Z_{n,t}. \end{aligned}$$

Then, $\mathbf{d}^T\,\mathbf{P}_{n0}=\mathbf{Q}_{n,1}+\mathbf{Q}_{n,2}+\mathbf{Q}_{n,3}$, where $\mathbf{Q}_{n,1}=\sum _{j=0}^{q_n-1}\eta _j$ and $\mathbf{Q}_{n,2}=\sum _{j=0}^{q_n-1}\zeta _j$. Next we prove the following four facts: (i) as $n\rightarrow \infty$,

$$\begin{aligned} E(\mathbf{Q}_{n,2})^2\rightarrow 0,\quad E(\mathbf{Q}_{n,3})^2\rightarrow 0, \end{aligned}$$

(17)

(ii) as $n\rightarrow \infty$ and $\theta ^2_d(t)$ defined as in (16), we have

$$\begin{aligned} \sum _{j=0}^{q_n-1}E\left( \eta _j^2\right) \rightarrow \theta ^2_d, \end{aligned}$$

(18)

(iii) for any $s$ and $n \rightarrow \infty$,

$$\begin{aligned} \left| E\left[ \exp (i\,s\,\mathbf{Q}_{n,1})\right] -\prod _{j=0}^{q_n-1}E\left[ \exp (i\,s\,\eta _j) \right] \right| \rightarrow 0, \end{aligned}$$

(19)

and (iv) for every $\varepsilon >0$,

$$\begin{aligned} \sum _{j=0}^{q_n-1}E\left[ \eta _j^2I\left\{ |\eta _j|\ge \varepsilon \,\theta _d\right\} \right] \rightarrow 0. \end{aligned}$$

(20)

(17) implies that $\mathbf{Q}_{n,2}$ and $\mathbf{Q}_{n,3}$ are asymptotically negligible in probability. (19) shows that the summands $\{\eta _j\}$ in $\mathbf{Q}_{n,1}$ are asymptotically independent, and (18) and (20) are the standard Lindeberg-Feller conditions for asymptotic normality of $\mathbf{Q}_{n,1}$ for the independent setup. The rest proof is to establish (17)–(20) and it can be done by following the almost same lines as those used in the Proof of Theorem 2 in Cai et al. (2000) with some modifications. This completes the Proof of Theorem 1. $\square$