Abstract
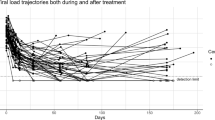
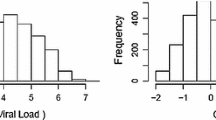
This paper presents an extension of the standard Tobit to simultaneously address segmental phases, subpopulation heterogeneity, lower limit of detection, and skewness in outcomes of human immunodeficiency virus (HIV) or acquired immunodeficiency syndrome (AIDS) longitudinal data. A major problem often encountered in an HIV/AIDS research is the development of drug resistance to antiretroviral (ARV) drug or therapy. For dealing with drug resistance problem, estimating the time at which drug resistance would develop is usually sought. Following ARV treatment, the profile of each subject’s viral load tends to follow a ‘broken stick’ like growth trajectory, indicating multiple phases of decline and increase in viral loads. Such multiple phases with multiple change-points are captured by subject-specific random parameters of growth curve models. To account subpopulation heterogeneity of drug resistance among patients, the turning-points are also allowed to differ by latent classes of patients on the basis of trajectories of observed viral loads. These features of viral longitudinal data are jointly modeled in a unified framework of segmental growth mixture Tobit mixed-effects models with skew distributions for a response variable with left censoring and skewness under the Bayesian approach. The proposed methods are illustrated using real data from an AIDS clinical study.




Similar content being viewed by others
References
Arabmazar A, Schmidt P (1982) An investigation of the robustness of the Tobit estimator to non-normality. Econometrica 50:1055–1064
Arellano-Valle RB, Genton MG (2005) On fundamental skew distributions. J Multivar Anal 96:93–116
Azzalini A, Capitanio A (1999) Statistical applications of the multivariate skew normal distributions. J R Stat Soc Ser B 61:579–602
Cudeck R, Harring JR (2010) Developing a random coefficient model for nonlinear repeated measures data. In: Chow S-M, Ferrer E, Hsieh F (eds) Statistical methods for modeling human dynamics: an interdisciplinary dialogue. Routledge, New York, pp 289–318
Dagne GA, Huang Y (2012) Bayesian inference for a nonlinear mixed-eefects Tobit model with multivariate skew-t distributions: application to AIDS studies. Int J Biostat 8(1), Article 27
Dagne GA, Huang Y (2013) Bayesian semiparametric mixture Tobit models with left-censoring, skewness and covariate measurement error. Stat Med 32:3881–3898
Gelman A, Carlin JB, Stern HS, Rubin DB (2004) Bayesian data analysis, 2nd edn. Chapman and Hall/CRC, New York
Genton MG (2004) Skew-elliptical distributions and their applications: a journey beyond normality. Chapman & Hall/CRC, Boca Raton
Greene W (2003) Econometric analysis. Prentice Hall, New Jersey
Ho DD, Neumann AU, Perelson AS, Chen W, Leonard JM, Markowitz M (1995) Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 373:123–126
Ho HJ, Lin TI (2010) Robust linear mixed models using the skew t distribution with application to schizophrenia data. Biom J 52:449–469
Hornung RW, Reed LD (1990) Estimation of average concentration in the presence of nondetectable values. Appl Occup Environ Hyg 4:46–51
Hughes JP (1999) Mixed effects models with censored data with application to HIV RNA levels. Biometrics 55:625–629
Kim YK, Muthén BO (2009) Two-part factor mixture modeling: application to an aggressive behavior measurement instrument. Struct Equ Model 16(4):602–624
Lederman MM, Connick E, Landay A, Kuritzkes DR, Spritzler J, Clair SM, Kotzin BL, Fox L, Chiozzi MH, Leonard JM, Rousseau F, Wade M, Roe JD, Martinez A, Kessler H (1998) Immunologic responses associated with 12 weeks of combination antiretroviral therapy consisting of zidovudine, lamivudine, and ritonavir: results of AIDS Clinical Trials Group Protocol 315. J Infect Dis 178:70–79
Lorimer MF, Kiermeier A (2007) Analysing microbiological data: Tobit or not Tobit? Int J Food Microbiol 116:313–318
Lunn DJ, Thomas A, Best N, Spiegelhalter D (2000) WinBUGS-a Bayesian modelling framework: concepts, structure, an extensibility. Stat Comput 10:325–337
McLachlan GJ, Peel D (2000) Finite mixture models. Wiley, New York
Muthén B (2004) Latent variable analysis: growth mixture modeling and related techniques for longitudinal data. In: Kaplan D (ed) Handbook of quantitative methodology for the social sciences. Sage, Newbury Park, pp 345–368
Nettles RE, Kieffer TL, Kwon P, Monie D, Han Y, Parsons T, Cofrancesco J Jr, Gallant JE, Quinn TC, Jackson B, Flexner C, Carson K, Ray S, Persaud D, Siliciano RF (2005) Intermittent HIV-1 viremia (blips) and drug resistance in patients receiving HAART. J Am Med Assoc 293:817–829
Ntzoufras I (2009) Bayesian modeling using WinBUGS. Wiley, New Jersey
Papasavvas E, Ortiz GM, Gross R, Sun J, Moore EC, Heymann JJ, Moonis M, Sandberg JK, Drohan LA, Gallagher B, Shull J, Nixon DF, Kostman JR, Montaner LJ (2000) Enhancement of human immunodeficiency virus type 1—specific CD4 and CD8 T cell responses in chronically infected persons after temporary treatment interruption. J Infect Dis 182(3):766–775
Paxton WB, Coombs RW, McElrath MJ, Keefer MC, Hughes J, Sinangil F, Chernoff D, Demeter L, Williams B, Corey L (1997) Longitudinal anlysis of quantitative virologic measures in human immunodeficiency virus-infected subjects with \(\ge \)400 CD4 lymphocytes: implication for applying measurements to individual patients. J Infect Dis 175:247–254
Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD (1996) HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 271:1582–1586
Ray N, Harrison JE, Blackburn LA, Martin JN, Deeks SG, Doms RW (2007) Clinical resistance to enfuvirtide does not affect susceptibility of human immunodeficiency virus type 1 to other classes of entry inhibitors. J Virol 81:3240–3250
Sahu SK, Dey DK, Branco MD (2003) A new class of multivariate skew distributions with applications to Bayesian regression models. Can J Stat 31:129–150
Schmidt P, Witte AD (1984) An economic analysis of crime and justice. Academic Press, Orlando
Schnedler W (2005) Likelihood estimation for censored random vectors. Econom Rev 24(2):195–217
Thisted RA (1988) Elements of statistical computing, numerical computation. Chapman and Hall, New York
Tobin J (1958) Estimation of relationships for limited dependent variables. Econometrica 26:24–36
Verbeke G, Lesaffre E (1996) A linear mixed-effects model with heterogeneity in random-effects population. J Am Stat Assoc 91:736–743
Wang WL, Fan TH (2012) Bayesian analysis of multivariate t linear mixed models using a combination of IBF and Gibbs samplers. J Multivar Anal 105:300–310
Wang WL, Lin TI (2014) Multivariate t nonlinear mixed-effects models for multi-outcome longitudinal data with missing values. Stat Med 33:3029–3046
Wang WL, Lin TI (2015) Bayesian analysis of multivariate t linear mixed models with missing responses at random. J Stat Comput Simul. doi:10.1080/00949655.2014.989852
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dagne, G.A. Bayesian segmental growth mixture Tobit models with skew distributions. Comput Stat 31, 121–137 (2016). https://doi.org/10.1007/s00180-015-0620-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-015-0620-8