Quasi-likelihood inference for self-exciting threshold integer-valued autoregressive processes

Abstract

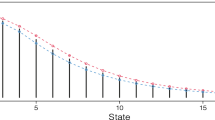
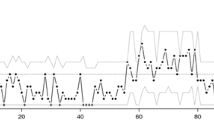
This article redefines the self-exciting threshold integer-valued autoregressive (SETINAR(2,1)) processes under a weaker condition that the second moment is finite, and studies the quasi-likelihood inference for the new model. The ergodicity of the new processes is discussed. Quasi-likelihood estimators for the model parameters and the asymptotic properties are obtained. Confidence regions of the parameters based on the quasi-likelihood method are given. A simulation study is conducted for the evaluation of the proposed approach and an application to a real data example is provided.

Appendix

Proof of Proposition 2.1

According to Theorem 3.1 of Tweedie (1975)(or Proposition 2.2 of Zheng and Basawa 2008), the sufficient condition of $\{X_t\}$ to be ergodic is that there exists a set K and a non-negative measurable function g on state space $\mathbb {N}_0$ such that

$$\begin{aligned} \int _{\mathbb {N}_0}P(x,dy)g(y)\le g(x)-1,~~x\notin K, \end{aligned}$$

(5.1)

and for some fixed B, 

$$\begin{aligned} \int _{\mathbb {N}_0}P(x,dy)g(y)=\lambda (x)\le B<\infty ,~~x\in K, \end{aligned}$$

(5.2)

where $P(x,A)=P(X_1\in A|X_0=x).$ Let $g(x)=x,$ we have

$$\begin{aligned} \int _{\mathbb {N}_0}g(y)dP(X_1=y|X_0=x_0)&=E(X_1|X_0=x_0) =\alpha _1x_0I_{0,1}+\alpha _2x_0I_{0,2}+\lambda \\&\le \alpha _{\max }x_0+\lambda , \end{aligned}$$

where $\alpha _{\max }=\max \{\alpha _1,\alpha _2\}<1.$ let $N=[\frac{1+\lambda }{1-\alpha _{\max }}]+1$, where [x] denotes the integer part of x. Then for $x_0\ge N,$ we have

$$\begin{aligned} \alpha _{\max }x_0+\lambda \le x_0-1=g(x_0)-1, \end{aligned}$$

and for $0\le x_0\le N-1,$

$$\begin{aligned} \int _{\mathbb {N}_0}g(y)dP(X_1=y|X_0=x_0)&=E(X_1|X_0=x_0) \le \alpha _{\max }x_0+\lambda \le N+\lambda <\infty . \end{aligned}$$

Let $K=\{0,1, \ldots ,N-1\},$ then (5.1) and (5.2) both hold which completes the proof. $\square$

Proof of Theorem 2.1

First, we suppose $\varvec{\theta }$ is known. Let $\mathcal {F}_t=\sigma (X_0,X_1, \ldots ,X_t)$ be the $\sigma$-field generated by $\{X_0,X_1, \ldots ,X_t\}$. For the following estimation equations:

$$\begin{aligned} S_n^{(1)}(\varvec{\theta },\varvec{\beta })=\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{1,t}X_{t-1}, \end{aligned}$$

we have

$$\begin{aligned}&E[V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{1,t}X_{t-1}|\mathcal {F}_{t-1}]\\&\quad =V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})I_{1,t}X_{t-1}E[(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )|\mathcal {F}_{t-1}]\\&\quad =0, \end{aligned}$$

and

$$\begin{aligned}&E[S_t^{(1)}(\varvec{\theta },\varvec{\beta })|\mathcal {F}_{t-1}]\\&\quad =E[(V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{1,t}X_{t-1}\\&\qquad +S_{t-1}^{(1)}(\varvec{\theta },\varvec{\beta }))|\mathcal {F}_{t-1}]\\&\quad =S_{t-1}^{(1)}(\varvec{\theta },\varvec{\beta }). \end{aligned}$$

Thus, $\{S_t^{(1)}(\varvec{\theta },\varvec{\beta }),\mathcal {F}_{t},~t\ge 0\}$ is a martingale. By (C1) and Theorem 1.1 in Billingsley (1961),

$$\begin{aligned}&\frac{1}{n}\sum _{t=1}^n V_{\varvec{\theta }}^{-2}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )^2X_{t-1}^2I_{1,t}\\&\quad \overset{a.s.}{\longrightarrow }E\left( V_{\varvec{\theta }}^{-2}(X_1|X_{0})(X_1-\alpha _1X_{0}I_{1,1}-\alpha _2X_{0}I_{2,1}-\lambda )^2X_0^2I_{1,1}\right) \\&\quad = E\left( E[V_{\varvec{\theta }}^{-2}(X_1|X_{0})(X_1-\alpha _1X_{0}I_{1,1}-\alpha _2X_{0}I_{2,1}-\lambda )^2X_0^2I_{1,1}|X_0]\right) \\&\quad = E[V_{\varvec{\theta }}^{-1}(X_1|X_0)X_0^2I_{1,1}]\\&\quad = T_{11}(\varvec{\theta }). \end{aligned}$$

Hence, by Corollary 3.2 in Hall and Heyde (1980) and the central limit theorem of martingale, we have,

$$\begin{aligned} \frac{1}{\sqrt{n}}S_n^{(1)}(\varvec{\theta },\varvec{\beta })\overset{L}{\longrightarrow }N(0,T_{11}(\varvec{\theta })). \end{aligned}$$

Similarly,

$$\begin{aligned} S_n^{(2)}(\varvec{\theta },\varvec{\beta })=\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{2,t}X_{t-1}, \end{aligned}$$

and

$$\begin{aligned} S_n^{(3)}(\varvec{\theta },\varvec{\beta })=\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda ), \end{aligned}$$

We can verify that $\{S_t^{(i)}(\varvec{\theta },\varvec{\beta }),\mathcal {F}_{t},~t\ge 0\}$ $(i=2,3)$ are also martingales. Similar to the previous discussion, we have

$$\begin{aligned} \frac{1}{\sqrt{n}}S_n^{(i)}(\varvec{\theta },\varvec{\beta })\overset{L}{\longrightarrow }N(0,T_{ii}(\varvec{\theta })),~i=2,3. \end{aligned}$$

By Cramer-Wold device, for any $\varvec{c}^\textsf {T}=(c_1,c_2,c_3) \in \mathbb {R}^3$ and $(c_1,c_2,c_3)\ne (0,0,0)$, we have

$$\begin{aligned} \frac{\varvec{c}^\textsf {T}}{\sqrt{n}}\left( \begin{array}{c} S_n^{(1)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(2)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(3)}(\varvec{\theta },\varvec{\beta }) \end{array}\right)&=\frac{1}{\sqrt{n}}\sum _{i=1}^3 c_iS_n^{(i)}(\varvec{\theta },\varvec{\beta })\\&=\frac{1}{\sqrt{n}}\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )\\&\quad \cdot (c_1I_{1,t}X_{t-1}+c_2I_{2,t}X_{t-1}+c_3)\\&\overset{L}{\longrightarrow } N(0,E[V_{\varvec{\theta }}^{-1}(X_1|X_0)(c_1 X_{0}I_{1,1}+c_2 X_{0}I_{2,1}+c_3)^2]), \end{aligned}$$

implying

$$\begin{aligned} \frac{1}{\sqrt{n}}\left( \begin{array}{c} S_n^{(1)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(2)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(3)}(\varvec{\theta },\varvec{\beta }) \end{array}\right)&\overset{L}{\longrightarrow } N\left( \varvec{0},\varvec{T}(\varvec{\theta })\right) . \end{aligned}$$

Now, we replace $V_{\varvec{\theta }}(X_t|X_{t-1})$ with $V_{\hat{\varvec{\theta }}}(X_t|X_{t-1})$, where $\hat{\varvec{\theta }}$ is a consistent estimator of ${\varvec{\theta }}$. Then we want

$$\begin{aligned} \frac{1}{\sqrt{n}}\left( \begin{array}{c} S_n^{(1)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(2)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(3)}(\hat{\varvec{\theta }},\varvec{\beta }) \end{array}\right)&\overset{L}{\longrightarrow } N\left( \varvec{0},\varvec{T}(\varvec{\theta })\right) . \end{aligned}$$

(5.3)

To prove (5.3), we need to check that

$$\begin{aligned} \frac{1}{\sqrt{n}}S_n^{(i)}(\hat{\varvec{\theta }},\varvec{\beta })-\frac{1}{\sqrt{n}}S_n^{(i)}({\varvec{\theta }},\varvec{\beta })\overset{P}{\longrightarrow }0,~i=1,2,3. \end{aligned}$$

(5.4)

Let $R_n(\varvec{\theta })=(1/\sqrt{n})S_n^{(1)}(\varvec{\theta },\varvec{\beta })$. Then for any $\varepsilon >0$ and $\delta >0$, we have

$$\begin{aligned} P(|R_n(\hat{\varvec{\theta }})-R_n(\varvec{\theta })|>\varepsilon )&\le \sum _{i=1}^2P(|\hat{\theta }_i-\theta _i|>\delta )+P(|\hat{\sigma }_z^2-\sigma _z^2|>\delta )\\&\quad +P(\sup _D|R_n(\varvec{\theta }_1)-R_n(\varvec{\theta })|>\varepsilon ), \end{aligned}$$

where $\varvec{\theta }_1=(\theta _1^{1},\theta _2^{1},\sigma _1^{2})^\textsf {T}, D:=\{|\theta _1^{1}-\theta _1|<\delta ,|\theta _2^{1}-\theta _2|<\delta ,|\sigma _1^{2}-\sigma _z^2|<\delta \}.$ If $\hat{\varvec{\theta }}$ is a consistent estimator of ${\varvec{\theta }}$, then we just need to prove that

$$\begin{aligned} P\left( \sup _D|R_n(\varvec{\theta }_1)-R_n(\varvec{\theta })|>\varepsilon \right) \overset{P}{\longrightarrow }0. \end{aligned}$$

By Markov inequality,

$$\begin{aligned}&P\left( \sup _D|R_n(\varvec{\theta }_1)-R_n(\varvec{\theta })|>\varepsilon \right) \nonumber \\&\quad \le \frac{1}{\varepsilon ^2}E\left( \sup _D(R_n(\varvec{\theta }_1)-R_n(\varvec{\theta }))^2\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D\frac{1}{n}\sum _{t=1}^n(V_{\varvec{\theta }_1}^{-1}(X_t|X_{t-1})-V_{\varvec{\theta }}^{-1}(X_t|X_{t-1}))^2 \left( X_t-\sum _{i=1}^2\alpha _iI_{i,t}X_{t-1}-\lambda \right) ^2X_{t-1}^2I_{1,t}\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D(V_{\varvec{\theta }_1}^{-1}(X_1|X_{0})-V_{\varvec{\theta }}^{-1}(X_1|X_{0}))^2 \left( X_1-\sum _{i=1}^2\alpha _iI_{i,t}X_{0}-\lambda \right) ^2X_{0}^2I_{1,1}\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D \frac{\left( \sum _{i=1}^2\left( \theta _i-\theta _i^1\right) X_0I_{i,1}+\left( \sigma _z^2-\sigma _1^2\right) \right) ^2}{V_{\varvec{\theta }_1}^{2}(X_1|X_{0})V_{\varvec{\theta }}^{2}(X_1|X_{0})} \left( X_1-\sum _{i=1}^2\alpha _iI_{i,t}X_{0}-\lambda \right) ^2X_{0}^2I_{1,1}\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D \frac{\left( \sum _{i=1}^2\left( \theta _i-\theta _i^1\right) X_0I_{i,1}+\left( \sigma _z^2-\sigma _1^2\right) \right) ^2}{V_{\varvec{\theta }_1}^{2}(X_1|X_{0})V_{\varvec{\theta }}(X_1|X_{0})} X_{0}^2I_{1,1}\right) \nonumber \\&\quad \le \frac{1}{\varepsilon ^2}\sup _D \left\{ ((\theta _1-\theta _1^1)^2 m_1 +(\theta _2-\theta _2^1)^2 m_2 +(\sigma _z^2-\sigma _1^2)^2 m_3 +2m_4|\theta _1-\theta _1^2||\theta _2-\theta _2^1|\right. \nonumber \\&\quad \quad \left. +2m_5|\theta _1-\theta _1^1||\sigma _z^2-\sigma _1^2|+2m_6|\theta _2-\theta _2^1||\sigma _z^2-\sigma _1^2|) X_{0}^2I_{1,1}\right\} \nonumber \\&\quad \le \frac{C\delta ^2}{\varepsilon ^2}, \end{aligned}$$

(5.5)

where $m_i~(i=1,2, \ldots ,6)$ denote some finite moments of process $\{X_t\}$, C is a positive constant. Similar argument can be used for $1/\sqrt{n}S_n^{(i)}(\varvec{\theta },\varvec{\beta })(i=2,3)$. For any fixed $\varepsilon >0$, letting $\delta \rightarrow 0$, we get our assertion which in turn establishes (5.3).

Finally, by the ergodic theorem, we have

$$\begin{aligned} \frac{1}{n}\varvec{Q}_n\overset{P}{\longrightarrow }\varvec{T}(\varvec{\theta }). \end{aligned}$$

After some algebra, we have,

$$\begin{aligned} (\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })=\varvec{Q}_n^{-1} \left( \begin{array}{c} S_n^{(1)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(2)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(3)}(\hat{\varvec{\theta }},\varvec{\beta }) \end{array}\right) , \end{aligned}$$

Therefore,

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })=\left( \frac{1}{n}\varvec{Q}_n\right) ^{-1} \frac{1}{\sqrt{n}} \left( \begin{array}{c} S_n^{(1)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(2)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(3)}(\hat{\varvec{\theta }},\varvec{\beta }) \end{array}\right) \overset{L}{\longrightarrow }N(\varvec{0},\varvec{T}^{-1}(\varvec{\theta })). \end{aligned}$$

(5.6)

The proof is complete. $\square$

Proof of Theorem 2.2

The proof follows by the ergodic theorem. $\square$

Proof of Theorem 2.3

The proof follows from Theorem 2.1. $\square$