Skip to main content
SpringerLink
Log in

Bivariate nonparametric estimation of the Pickands dependence function using Bernstein copula with kernel regression approach

  • Original Paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

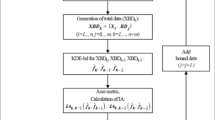
In this study, a new nonparametric approach using Bernstein copula approximation is proposed to estimate Pickands dependence function. New data points obtained with Bernstein copula approximation serve to estimate the unknown Pickands dependence function. Kernel regression method is then used to derive an intrinsic estimator satisfying the convexity. Some extreme-value copula models are used to measure the performance of the estimator by a comprehensive simulation study. Also, a real-data example is illustrated. The proposed Pickands estimator provides a flexible way to have a better fit and has a better performance than the conventional estimators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Aguilera N, Forzani L, Morin P (2011) On uniform consistent estimators for convex regression. J Non-parametr Stat 23(4):897–908

    Article  MATH  MathSciNet  Google Scholar 

  • Ahmadabadi A, Ucer Hudaverdi B (2015) Nonparametric estimation for dependence function of some bivariate extreme value copulas with Bernstein polynomials. EMS 2015, European Meeting of Statisticians Amsterdam, July 6–10, Program and Book of Abstracts, pp 90

  • Barber CB, Dobkin DP, Huhdanpaa HT (1996) The Quickhull algorithm for convex hulls. ACM Trans Math Softw 22(4):469–483

    Article  MATH  MathSciNet  Google Scholar 

  • Bücher A, Dette H, Volgushev S (2011) New estimators of the Pickands dependence function and a test for extreme-value dependence. Ann Stat 39:1963–2006

    Article  MATH  MathSciNet  Google Scholar 

  • Capera P, Fougeres A-L, Genest C (1997) A nonparametric estimation procedure for bivariate extreme value copulas. Biometrika 84:567–577

    Article  MATH  MathSciNet  Google Scholar 

  • Cormier E, Genest C, Nevslehova JG (2014) Using B-splines for nonparametric inference on bivariate extreme-value copulas. Extremes 17:633–659

    Article  MATH  MathSciNet  Google Scholar 

  • Deheuvels P (1991) On the limiting behavior of the Pickands estimator for bivariate extreme-value distributions. Stat Probab Lett 12:429–439

    Article  MATH  MathSciNet  Google Scholar 

  • Frees EW, Valdez EA (1998) Understanding relationships using copulas. N Am Actuar J 2:1–25

    Article  MATH  MathSciNet  Google Scholar 

  • Genest C, Segers J (2009) Rank-based inference for bivariate extreme-value copulas. Ann Stat 37:2990–3022

    Article  MATH  MathSciNet  Google Scholar 

  • Gumbel EJ (1960) Distributions des valeurs extremes en plusieurs dimensions. Publ Inst Stat Univ Paris 9:171–173

    MATH  MathSciNet  Google Scholar 

  • Hall P, Tajvidi N (2000) Distribution and dependence-function estimation for bivariate extreme-value distributions. Bernoulli 6:835–844

    Article  MATH  MathSciNet  Google Scholar 

  • Janssen P, Swanepoel J, Veraverbeke N (2012) Large sample behavior of the Bernstein copula estimator. J Stat Plann Inference 142:1189–1197

    Article  MATH  MathSciNet  Google Scholar 

  • Marcon G, Padoan SA, Naveau P, Muliere P (2014) Multivariate nonparametric estimation of the Pickands dependence function using Bernstein polynomials. arXiv preprint arXiv:1405.5228

  • Nadaraya EA (1964) On estimating regression. Theory Probab Appl 9(1):141–142

    Article  MATH  Google Scholar 

  • Pickands J (1981) Multivariate extreme value distribution. In: Proceedings of the 43rd session of the I.S.I. International Statistical Institute, pp 859–878

  • Sancetta A, Satchell S (2004) The Bernstein copula and its application to modeling and approximations of multivariate distributions. Econom Theory 3:535–562

    MATH  MathSciNet  Google Scholar 

  • Sancetta A (2007) Nonparametric estimation of distributions with given marginals via Bernstein-Kantorovich polynomials: L1 and pointwise convergence theory. J Multivar Anal 98(7):1376–1390

    Article  MATH  MathSciNet  Google Scholar 

  • Segers J (2007) Non-parametric inference for bivariate extreme-value copulas. In: Ahsanullah M, Kirmani S (eds) Extreme value distributions. Nova Science, New York, pp 181–203

    Google Scholar 

  • Sklar A (1959) Fonctions de répartition à n dimensions et leurs marges. Publ Inst Stat Univ Paris 8:229–231

    MATH  Google Scholar 

  • Tawn JA (1988) Bivariate extreme value theory: models and estimation. Biometrika 75:397–415

    Article  MATH  MathSciNet  Google Scholar 

  • Watson GS (1964) Smooth regression analysis. Sankhya: Indian J Stat Ser A 26(4):359–372

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Statistics, Faculty of Sciences, Dokuz Eylul University, Izmir, Turkey

    Alireza Ahmadabadi & Burcu Hudaverdi Ucer

Authors
  1. Alireza Ahmadabadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Burcu Hudaverdi Ucer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Burcu Hudaverdi Ucer.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmadabadi, A., Ucer, B.H. Bivariate nonparametric estimation of the Pickands dependence function using Bernstein copula with kernel regression approach. Comput Stat 32, 1515–1532 (2017). https://doi.org/10.1007/s00180-017-0750-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-017-0750-2

Keywords

Search

Navigation