Skip to main content
Springer Nature Link
Log in

Geometric ergodicity of a Metropolis-Hastings algorithm for Bayesian inference of phylogenetic branch lengths

  • Original paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

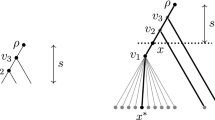
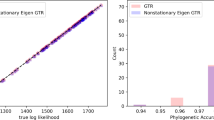
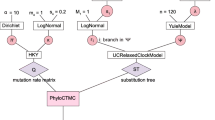
This manuscript extends the work of Spade et al. (Math Biosci 268:9–21, 2015) to an examination of a fully-updating version of a Metropolis-Hastings algorithm for inference of phylogenetic branch lengths. This approach serves as an intermediary between theoretical assessment of Markov chain convergence, which in phylogenetic settings is typically difficult to do analytically, and output-based convergence diagnostics, which suffer from several of their own limitations. In this manuscript, we will also examine the performance of the convergence assessment techniques for this Markov chain and the convergence behavior of this type of Markov chain compared to the one-at-a-time updating scheme investigated in Spade et al. (Math Biosci 268:9–21, 2015). We will also vary the choices of the drift function in order to obtain a sense of how the choice of the drift function affects the estimated bound on the chain’s mixing time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Allman E, Ané C, Rhodes J (2008) Identifiability of a markovian model of molecular evolution with gamma-distributed rates. Adv Appl Probab 40:229–249

    MathSciNet  MATH  Google Scholar 

  • Binet M, Gascuel O, Scornavacca C, Douzery EJP, Pardi F (2016) Fast and accurate branch lengths estimation for phylogenomic trees. BMC Bioinform 17:23–40

    Google Scholar 

  • Bryant D, Waddell P (1998) Rapid evaluation of least-squares and minimum-evolution criteria on phylogenetic trees. Mol Biol Evol 15:1346–1359

    Google Scholar 

  • Camin JH, Sokal RR (1965) A method for deducing branching sequences in phylogeny. Evolution 19:311–326

    Google Scholar 

  • Cavalli-Sforza LL, Edwards AWF (1965) Analysis of human evolution. In: Genetics today, proceedings of the XI international congress of genetics, The Hague, Netherlands

  • Cavalli-Svorza LL, Edwards AWF (1967) Phylogenetic analysis: models and estimation procedures. Am J Hum Genet 19:233–257

    Google Scholar 

  • Chib S, Nardari F, Shephard N (1998) Markov chain monte carlo methods for generalized stochastic volatility models. J Econom 108:281–316

    MATH  Google Scholar 

  • Cowles MK, Carlin BP (1996) Markov chain monte carlo convergence diagnostics: a comparative review. J Am Stat Assoc 91:883–904

    MathSciNet  MATH  Google Scholar 

  • Cowles MK, Rosenthal JS (1998) A simulation-based approach to convergence rates for markov chain monte carlo algorithms. Stat Comput 8:115–124

    Google Scholar 

  • Drummond AJ, Suchard MA, Xie D, Rambaut A (2012) Bayesian phylogenetics with BEAUti and the BEAST 17. Molecul Biol Evol 29(8):1969–1973

    Google Scholar 

  • Eck RV, Dayhoff MO (1966) Atlas of protein sequence and structure. National Biomedical Research Foundation, Silver Spring

    Google Scholar 

  • Edwards AWF, Cavalli-Sforza LL (1964) Reconstruction of evolutionary trees. Phen Phylogen Classif, pp 67–76

  • Edwards AWF (1970) Estimation of the branch points of a branching diffusion process. J Roy Stat Soc B 32:155–174

    MathSciNet  MATH  Google Scholar 

  • Felsenstein J (1981) Evolutionary trees from DNA sequences: a maximum likelihood approach. J Mol Evol 17:368–376

    Google Scholar 

  • Fitch WM, Margoliash E (1967) Construction of phylogenetic trees. Science 155:279–284

    Google Scholar 

  • Fort G, Moulines G, Roberts GO, Rosenthal JS (2003) On the geometric ergodicity of hybrid samplers. J Appl Probab 40:123–146

    MathSciNet  MATH  Google Scholar 

  • Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences. Stat Sci 7:457–511

    MATH  Google Scholar 

  • Gelman A, Roberts GO, Gilks WR (1996) Efficient metropolis jumping rules. Bayesian. Stat 5:599–607

    Google Scholar 

  • Geweke J (1992) Evaluating the accuracy of sampling-based approaches to calculating posterior moments. In: Bernardo JM, Berger J, Dawid AP, Smith AFM (eds) Bayesian statistics 4. Oxford University Press, Oxford

    Google Scholar 

  • Harper CW (1979) A Bayesian probability view of phylogenetic systematics. Syst Zool 28:547–553

    Google Scholar 

  • Hastings W (1970) Monte Carlo sampling techniques using markov chains and their applications. Biometrika 57:97–109

    MathSciNet  MATH  Google Scholar 

  • Heidelberger P, Welch PD (1983) Simulation run length control in the presence of an initial transient. Oper Res 31:1109–1144

    MATH  Google Scholar 

  • Huelsenbeck JP, Ronquist F (2001) MRBAYES: Bayesian inference of phylogeny. Bioinformatics 17:754–755

    Google Scholar 

  • Ishwaran H, James LF, Sun J (2001) Bayesian model selection and finite mixtures by marginal density decompositions. J Am Stat Assoc 96:1316–1332

    MathSciNet  MATH  Google Scholar 

  • Jarner SF, Hansen E (2000) Geometric ergodicity of metropolis algorithms. Stoch Process Appl 85:341–361

    MathSciNet  MATH  Google Scholar 

  • Jones G, Hobert JP (2001) Honest exploration of intractable probability distributions via markov chain monte carlo. Stat Sci 16(4):312–334

    MathSciNet  MATH  Google Scholar 

  • Jukes T, Cantor C (1969) Evolution of protein molecules. Mammalian protein metabolism, vol III. Academic Press, New York, pp 21–32

  • Kluge AG, Farris JS (1969) Phyletics and the evolution of anurans. Syst Zool 18:1–32

    Google Scholar 

  • Li H, Homer N (2010) A survey of sequence alignment algorithms for next-generation sequencing. Brief Bioinform 11:473–483

    Google Scholar 

  • Li S, Pearl DK, Doss H (2000) Phylogenetic tree construction using markov chain monte carlo. J Am Stat Assoc 95:493–508

    Google Scholar 

  • Liang F (2007) Continuous contour monte carlo for marginal density estimation with an application to a spatial statistical model. J Comput Graph Stat 16(3):608–632

    MathSciNet  Google Scholar 

  • Madras N, Sezer D (2010) Quantitative bounds for markov chain convergence: wasserstein and total variation distances. Bernoulli 16(3):882–908

    MathSciNet  MATH  Google Scholar 

  • Mau B, Newton MA (1997) Phylogenetic inference for binary data on dendograms using markov chain monte carlo. J Comput Graph Stat 6:122–131

    Google Scholar 

  • Mengersen KL, Tweedie RL (1996) Rates of convergence of the hastings and metropolis algorithms. Ann Stat 24(1):101–121

    MathSciNet  MATH  Google Scholar 

  • Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E (1953) Equations of state calculations by fast computing machines. J Chem Phys 21:1087–1092

    MATH  Google Scholar 

  • Neal RM (1998) Annealed importance sampling. Technical report, University of Toronto Department of Statistics

  • Needleman SB, Wunsch CD (1970) A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol 48(3):443–453

    Google Scholar 

  • Oh M, Berger JO (1989) Adaptive importance sampling in monte carlo integration. Techincal report, Purdue University Department of Statistics

  • Rannala B, Zhu T, Yang Z (2012) Tail paradox, partial identifiability, and influential priors in bayesian branch length inference. Mol Biol Evol 29(1):325–335

    Google Scholar 

  • Redelings BD, Suchard MA (2005) Joint Bayesian estimation of alignment and phylogeny. Syst Biol 54(3):401–418

    Google Scholar 

  • Roberts GO, Tweedie RL (1996) Geometric convergence and central limit theorems for multidimensional hastings and metropolis algorithms. Biometrika 83(1):95–110

    MathSciNet  MATH  Google Scholar 

  • Ronquist F, Teslenko M, van der Mark P, Ayres DL, Darling A, Hohna S, Larget B, Liu L, Suchard MA, Huelsenbeck JP (2012) MrBayes 32: efficient bayesian phylogenetic inference and model choice across a large model space. Syst Biol 61(3):539–542

    Google Scholar 

  • Rosenthal JS (1995) Minorization conditions and convergence rates for markov chain monte carlo. J Am Stat Assoc 90:558–566

    MathSciNet  MATH  Google Scholar 

  • Sankoff D (1972) Matching sequences under insertion-deletion constraints. Proc Nat Acad Sci USA 66:4–6

    MATH  Google Scholar 

  • Spade DA (2016) A computational procedure for efficient estimation of the convergence rate of the random-scan metropolis algorithm. Stat Comput 26(4):745–760

    MathSciNet  Google Scholar 

  • Spade DA, Herbei R, Kubatko LS (2015) Geometric ergodicity of a hybrid sampler for bayesian inference of phylogenetic branch lengths. Math Biosci 268:9–21

    MathSciNet  MATH  Google Scholar 

  • Steel M, Hein JJ (2001) A generalization of the thorne-kishino-felsenstein model for statistical alignment to k sequences related by a star tree. Lett Appl Math 14:679–684

    MATH  Google Scholar 

  • Tamura K, Nei M (1993) Estimation of the number of nucleotide substitutions in the control region of mitochondrial dna in humans and chimpanzees. Mol Biol Evol 10:612–626

    Google Scholar 

  • Tavare S (1986) Some probabilistic and statistical problems in the analysis of DNA sequences. In: Lectures on mathematics in the life sciences. American Mathematical Society, pp 57–86

  • Thompson KL, Kubatko LS (2013) Using ancestral information to detect and localize quantitative trait loci in genome-wide association studies. BMC Bioinform 14:200

    Google Scholar 

  • Yang Z, Rannala B (1997) Bayesian phylogenetic inference using DNA sequences: a markov chain monte carlo approach. Mol Biol Evol 14:717–724

    Google Scholar 

  • Yu B, Mykland P (1994) Looking at markov samplers through CUSUM path plots: a simple diagnostic idea. Technical report 413, University of California at Berkeley Department of Statistics

  • Zander R (2001) A conditional probability of reconstruction measure for internal cladogram branches. Syst Biol 50:425–437

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Wisconsin–Milwaukee, 3200 North Cramer Street, Milwaukee, WI, 53201, USA

    David A. Spade

Authors
  1. David A. Spade
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to David A. Spade.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work has been supported in part by National Science Foundation Grant NSF-DMS-1228244.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Spade, D.A. Geometric ergodicity of a Metropolis-Hastings algorithm for Bayesian inference of phylogenetic branch lengths. Comput Stat 35, 2043–2076 (2020). https://doi.org/10.1007/s00180-020-00969-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-020-00969-1

Keywords