Skip to main content
Springer Nature Link
Log in

Bayesian ridge estimators based on copula-based joint prior distributions for regression coefficients

  • Original paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

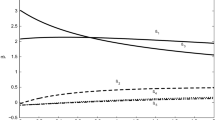
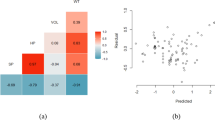
Abstract

Ridge regression is a widely used method to mitigate the multicollinearly problem often arising in multiple linear regression. It is well known that the ridge regression estimator can be derived from the Bayesian framework by the posterior mode under a multivariate normal prior. However, the ridge regression model with a copula-based multivariate prior model has not been employed in the Bayesian framework. Motivated by the multicollinearly problem due to an interaction term, we adopt a vine copula to construct the copula-based joint prior distribution. For selected copulas and hyperparameters, we propose Bayesian ridge estimators and credible intervals for regression coefficients. A simulation study is carried out to compare the performance of four different priors (the Clayton, Gumbel, and Gaussian copula priors, and the tri-variate normal prior) on the regression coefficients. Our simulation studies demonstrate that the Archimedean (Clayton and Gumbel) copula priors give more accurate estimates in the presence of multicollinearity compared with the other priors. Finally, a real dataset is analyzed, where the Bayesian ridge estimators and some frequentist estimators are compared.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Aas K, Czado C, Frigessi A, Bakken H (2009) Pair-copula constructions of multiple dependence. Insur Math Econ 44:182–198

    MathSciNet  MATH  Google Scholar 

  • Abonazel MR, Taha IM (2021) Beta ridge regression estimators: simulation and application. Commun Stat Simul Comput. https://doi.org/10.1080/03610918.2021.1960373

    Article  Google Scholar 

  • Allen DM (1974) The relationship between variable selection and data augmentation and a method for prediction. Technometrics 16:125–127

    MathSciNet  MATH  Google Scholar 

  • Armagan A, Zaretzki RL (2010) Model selection via adaptive shrinkage with t priors. Comput Stat 25:441–461

    MathSciNet  MATH  Google Scholar 

  • Assaf AG, Tsionas M, Tasiopoulos A (2019) Diagnosing and correcting the effects of multicollinearity: Bayesian implications of ridge regression. Tour Manag 71:1–8

    Google Scholar 

  • Bedford T, Cooke RM (2002) Vines: a new graphical model for dependent random variables. Ann Stat 30:1031–1068

    MathSciNet  MATH  Google Scholar 

  • Box GEP, Tiao GC (1992) Bayesian inference in statistical analysis. Wiley, New York

    MATH  Google Scholar 

  • Burzykowski T, Molenberghs G, Buyse M, Geys H, Renard D (2001) Validation of surrogate end points in multiple randomized clinical trials with failure time end points. J R Stat Soc Ser C (Appl Stat) 50(4):405–422

    MathSciNet  MATH  Google Scholar 

  • Chang B, Joe H (2019) Prediction based on conditional distributions of vine copulas. Comput Stat Data Anal 139:45–63

    MathSciNet  MATH  Google Scholar 

  • Chipman H (1996) Bayesian variable selection with related predictors. Can J Stat 24:17–36

    MathSciNet  MATH  Google Scholar 

  • Clayton DG (1978) A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 65:141–151

    MathSciNet  MATH  Google Scholar 

  • Czado C (2019) Analyzing dependent data with vine copulas. Lecture notes in statistics. Springer, Cham

    MATH  Google Scholar 

  • Emura T, Sofeu C, Rondeau V (2021) Conditional copula models for correlated survival endpoints: individual patient data meta-analysis of randomized controlled trials. Stat Methods Med Res 30(12):2634–2650

    MathSciNet  Google Scholar 

  • Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences. Stat Sci 7:457–511

    MATH  Google Scholar 

  • Griffin JE, Brown PJ (2013) Some priors for sparse regression modelling. Bayesian Anal 8:691–702

    MathSciNet  MATH  Google Scholar 

  • Griffin J, Brown P (2017) Hierarchical shrinkage priors for regression models. Bayesian Anal 12:135–159

    MathSciNet  MATH  Google Scholar 

  • Gumbel EJ (1960) Distributions des valeurs extremes en plusieurs dimensions. Publications De L’institut De Statistique De L’universit De Paris 9:171–173

    MathSciNet  MATH  Google Scholar 

  • Haff IH, Aas K, Frigessi A (2010) On the simplified pair-copula construction—simply useful or too simplistic? J Multivar Anal 101:1296–1310

    MathSciNet  MATH  Google Scholar 

  • Hans C (2011) Elastic net regression modeling with the orthant normal prior. J Am Stat Assoc 106:1383–1393

    MathSciNet  MATH  Google Scholar 

  • Hoerl AE, Kennard RW (1970) Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12:55–67

    MATH  Google Scholar 

  • Hoerl AE, Kannard RW, Baldwin KF (1975) Ridge regression: some simulations. Commun Stat 4:105–123

    MATH  Google Scholar 

  • Huard D, Evin G, Favre AC (2006) Bayesian copula selection. Comput Stat Data Anal 51:809–822

    MathSciNet  MATH  Google Scholar 

  • Joe H (1997) Multivariate models and dependence concepts. Chapman & Hall, London

    MATH  Google Scholar 

  • Joe H (2006) Generating random correlation matrices based on partial correlations. J Multivar Anal 97(10):2177–2189

    MathSciNet  MATH  Google Scholar 

  • Killiches M, Kraus D, Czado C (2017) Examination and visualisation of the simplifying assumption for vine copulas in three dimensions. Aust N Z J Stat 59(1):95–117

    MathSciNet  MATH  Google Scholar 

  • Kurowicka D, Cooke R (2003) A parameterization of positive definite matrices in terms of partial correlation vines. Linear Algebra Appl 372:225–251

    MathSciNet  MATH  Google Scholar 

  • Kurowicka D, Cooke RM (2006) Uncertainty analysis with high dimensional dependence modelling. Wiley, Hoboken

    MATH  Google Scholar 

  • Lewandowski D, Kurowicka D, Joe H (2009) Generating random correlation matrices based on vines and extended onion method. J Multivar Anal 100:1989–2001

    MathSciNet  MATH  Google Scholar 

  • Loesgen KH (1990) A generalization and Bayesian interpretation of ridge-type estimators with good prior means. Stat Pap 31:147–154

    MathSciNet  MATH  Google Scholar 

  • Michimae H, Matsunami M, Emura T (2020) Robust ridge regression for estimating the effects of correlated gene expressions on phenotypic traits. Environ Ecol Stat 27:41–72

    Google Scholar 

  • Mitchell TJ, Beauchamp JJ (1988) Bayesian variable selection in linear regression. J Am Stat Assoc 83:1023–1032

    MathSciNet  MATH  Google Scholar 

  • Montgomery DC, Peck EA, Vining GG (2012) Introduction to linear regression analysis, 5th edn. Wiley, Hoboken

    MATH  Google Scholar 

  • Nelsen RB (2006) An introduction to copulas. Springer series in statistics. Springer, New York

    Google Scholar 

  • Norouzirad M, Arashi M (2019) Preliminary test and Stein-type shrinkage ridge estimators in robust regression. Stat Pap 60:1849–1882

    MathSciNet  MATH  Google Scholar 

  • Nikoloulopoulos AK (2017) A vine copula mixed effect model for trivariate meta-analysis of diagnostic test accuracy studies accounting for disease prevalence. Stat Methods Med Res 26:2270–2286

    MathSciNet  Google Scholar 

  • O’Brien RM (2007) A caution regarding rules of thumb for variance inflation factors. Qual Quant 41:673–690

    Google Scholar 

  • Park T, Casella G (2008) The Bayesian lasso. J Am Stat Assoc 103(482):681–686

    MathSciNet  MATH  Google Scholar 

  • Pliskin JL (1987) A ridge-type estimator and good prior means. Commun Stat Theory Methods 16:3429–3437

    MathSciNet  MATH  Google Scholar 

  • Polson NG, Scott JG (2012) On the half-Cauchy prior for a global scale parameter. Bayesian Anal 7:887–902

    MathSciNet  MATH  Google Scholar 

  • Salmerón R, García J, García C, del Mar LM (2018) Transformation of variables and the condition number in ridge estimation. Comput Stat 33:1497–1524

    MathSciNet  MATH  Google Scholar 

  • Sambasivan R, Das S, Sahu SK (2020) A Bayesian perspective of statistical machine learning for big data. Comput Stat 35:893–930

    MathSciNet  MATH  Google Scholar 

  • Scheipl F, Kneib T, Fahrmeir L (2013) Penalized likelihood and Bayesian function selection in regression models. Adv Stat Anal 97:349–385

    MathSciNet  MATH  Google Scholar 

  • Schepsmeier U, Stöber J (2014) Derivatives and Fisher information of bivariate copulas. Stat Pap 55:525–542

    MathSciNet  MATH  Google Scholar 

  • Shih JH, Lin TY, Jimichi M, Emura T (2021) Robust ridge M-estimators with pretest and Stein-rule shrinkage for an intercept term. Jpn J Stat Data Sci 4:107–150

    MathSciNet  MATH  Google Scholar 

  • Stan Development Team (2017) Stan modeling language users guide and reference manual. https://mc-stan.org

  • Stan Development Team (2018) RStan: the R interface to Stan. R package version 2.17.3. http://mc-stan.org

  • Stöber J, Joe H, Czado C (2013) Simplified pair copula constructions—limitations and extensions. J Multivar Anal 119:101–118

    MathSciNet  MATH  Google Scholar 

  • van Wieringen WN (2021) Lecture notes on ridge regression. arXiv preprint https://arxiv.org/pdf/1509.09169

  • Veerman JR, Leday GG, van de Wiel MA (2022) Estimation of variance components, heritability and the ridge penalty in high-dimensional generalized linear models. Commun Stat Simul Comput 51(1):116–134

    MathSciNet  MATH  Google Scholar 

  • Wong KY, Chiu SN (2015) An iterative approach to minimize the mean squared error in ridge regression. Comput Stat 30(2):625–639

    MathSciNet  MATH  Google Scholar 

  • Yang SP, Emura T (2017) A Bayesian approach with generalized ridge estimation for high-dimensional regression and testing. Commun Stat Simul Comput 46(8):6083–6105

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank Editor, Associate Editor, and two referees for their valuable suggestions that improved the paper. This research was supported by JSPS KAKENHI Grant Number JP21K12127.

Author information

Authors and Affiliations

  1. Department of Clinical Medicine (Biostatistics), School of Pharmacy, Kitasato University, Tokyo, 108-8641, Japan

    Hirofumi Michimae

  2. Biostatistics Center, Kurume University, 67 Asahi-machi, Kurume, Japan

    Takeshi Emura

Authors
  1. Hirofumi Michimae
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Takeshi Emura
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hirofumi Michimae.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Michimae, H., Emura, T. Bayesian ridge estimators based on copula-based joint prior distributions for regression coefficients. Comput Stat 37, 2741–2769 (2022). https://doi.org/10.1007/s00180-022-01213-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-022-01213-8

Keywords