Abstract
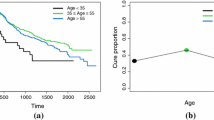
A new survival model is proposed in the presence of surviving fractions and unobserved dispersion. It is obtained by considering several latent factors (or risks) that generated the observed lifetime which follows a generalized Poisson distribution, and it includes as a special case, the promotion time cure model. We explore maximum likelihood tools for inference issues by aid of the expectation maximization algorithm for estimating the parameters while model discrimination problem is treated by the aid of the likelihood ratio test. The new regression is applied to cervical cancer data to evaluate covariates effects in the cured fraction and non-cured group.






Similar content being viewed by others
References
Ambagaspitiya R, Balakrishnan N (1994) On the compound generalized Poisson distributions. ASTIN Bull 24:255–263
Barriga GD, Cancho VG, Garibay DV, Cordeiro GM, Ortega EMM (2018) A new survival model with surviving fraction: An application to colorectal cancer data. Stat Methods Med Res 28:2665–2680
Berkson J, Gage RP (1952) Survival curve for cancer patients following treatment. J Am Stat Assoc 47:501–515
Cancho VG, Rodrigues J, de Castro M (2011) A flexible model for survival data with a cure rate: a Bayesian approach. J Appl Stat 38:57–70
Cancho VG, Macera MA, Suzuki AK, Louzada-Neto F, Zavaleta KE (2020) A new long-term survival model with dispersion induced by discrete frailty. Lifetime Data Anal 26:221–244
Cancho VG, Barriga GD, Cordeiro GM, Ortega EMM, Suzuki AK (2021) Bayesian survival model induced by frailty for lifetime with long-term survivors. Stat Neerl 75:299–323
Consul P, Jain G (1973) On a generalization of the Poisson distribution. Technometrics 15:791–799
Cordeiro GM, Cancho VG, Ortega EMM, Barriga GDC (2016) A model with long-term survivors: negative binomial Birnbaum–Saunders. Commun Stat Theory Methods 45:1370–1387
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE (1996) On the Lambert W function. Adv Comput Math 5:329–359
de Souza D, Cancho VG, Rodrigues J, Balakrishnan N (2017) Bayesian cure rate models induced by frailty in survival analysis. Stat Methods Med Res 26:2011–2028
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B (Methodol) 39:1–38
Dunn PK, Smyth GK (1996) Randomized quantile residuals. J Comput Graph Stat 5:236–244
Jodrá P (2010) Computer generation of random variables with Lindley or Poisson-Lindley distribution via the Lambert W function. Math Comput Simul 81:851–859
Maller RA, Zhou X, Zhou X (1996) Survival analysis with long-term survivors. Wiley, New York
McLachlan G, Krishnan T (2007) The EM algorithm and extensions, vol 382. Wiley, New York
Ortega EMM, Cordeiro GM, Campelo AK, Kattan MW, Cancho VG (2015) A power series beta Weibull regression model for predicting breast carcinoma. Stat Med 34:1366–1388
Pescim RR, Ortega EMM, Suzuki AK, Cancho VG, Cordeiro GM (2019) A new destructive Poisson odd log-logistic generalized half-normal cure rate model. Commun Stat Theory Methods 48:2113–2128
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007) Numerical recipes. The art of scientific computing, 3rd edn. Cambridge University Press, Cambridge
R Core Team (2022) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria
Ramires TG, Hens N, Cordeiro GM, Ortega EMM (2018) Estimating nonlinear effects in the presence of cure fraction using a semi-parametric regression model. Comput Stat 33:709–730
Rigby RA, Stasinopoulos DM (2005) Generalized additive models for location, scale and shape (with discussion). Appl Stat 54:507–554
Self S, Liang K (1987) Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Stat Assoc 82:605–610
Siva GO, Cordeiro GM, Ortega EMM (2020) Surviving and non surviving fraction regression models based on the beta modified Weibull distribution. Model Assist Stat Appl 15:111–126
Yakovlev A, Yu AB, Bardou V-J, Fourquet A, Hoang T, Rochefodiere A, Tsodikov AD (1993) A simple stochastics model of tumor recurrence an its aplications to data on premenopausal breast cancer. In: de Biometrie SF (ed) Biometrie et Analyse de Donnes Spatio-Temporelles No 12, B. France, pp 33–82
Yakovlev AY, Tsodikov AD (1996) Stochastic models of tumor latency and their biostatistical applications. World Scientific, New Jersey
Acknowledgements
The research of this paper was supported by grant from Brazilian agencies (CAPES and CNPq). CNPq Scholarship—Brazil (166774/2020-0)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Cancho, V.G., Bedia, E.C., Cordeiro, G.M. et al. A survival regression with cure fraction applied to cervical cancer. Comput Stat 38, 403–418 (2023). https://doi.org/10.1007/s00180-022-01233-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-022-01233-4