Skip to main content
Springer Nature Link
Log in

Bayesian estimation versus maximum likelihood estimation in the Weibull-power law process

  • Original paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

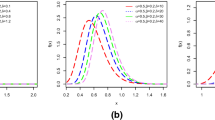
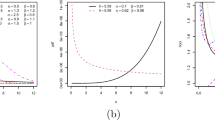
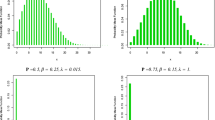
The Bayesian approach is applied to estimation of the Weibull-power law process (WPLP) parameters as an alternative to the maximum likelihood (ML) method in the case when the number of events is small. For the process model considered we propose to apply the independent Jeffreys prior distribution and we argue that this is a useful choice. Comparisons were also made between the accuracy of the estimators obtained and those obtained by using other priors—informative and weakly informative. The investigations show that the Bayesian approach in many cases of a fairly broad collection of WPLP models can lead to the Bayes estimators that are more accurate than the corresponding ML ones, when the number of events is small. The problem of fitting the WPLP models, based on ML and Bayes estimators, to some real data is also considered. It is shown that the TTT-concept, used in the reliability theory, is not fully useful for the WPLP models, and it may be so for some other trend-renewal processes. In order to assess the accuracy of the fitting to the real data considered, two other graphical methods are introduced.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28

Similar content being viewed by others

References

  • Aminzadeh MS (2013) Bayesian estimation of the expected time of first arrival past a truncated time T: the case of NHPP with power law intensity. Comput Stat 28:2465–2477

    MathSciNet  MATH  Google Scholar 

  • Andersen PK, Borgan Ø, Gill RD, Keiding N (1993) Statistical models based on counting processes. Springer series in statistics. Springer, New York

    MATH  Google Scholar 

  • Bandyopadhyay N, Sen S (2005) Non-standard asymptotics in an inhomogeneous gamma process. Ann Inst Stat Math 57(4):703–732

    MathSciNet  MATH  Google Scholar 

  • Bar-Lev SK, Lavi I, Reiser B (1992) Bayesian inference for the power law process. Ann Inst Stat Math 44(4):623–639

    MATH  Google Scholar 

  • Barlow RE, Campo R (1975) Total time on test processes and applications to failure data analysis. In: Reliability and fault tree analysis (Conf., Univ. California, Berkeley, Calif.), pp 451–481 (1974)

  • Bebbington MS (2013) Assessing probabilistic forecasts of volcanic eruption onsets. Bull Volcanol 75:783

    Google Scholar 

  • Bergman B, Klefsjö B (1984) The total time on test concept and its use in reliability theory. Oper Res 32(3):596–606

    MathSciNet  MATH  Google Scholar 

  • Brémaud P (1981) Point processes and queues. Springer, New York. Martingale Dynamics, Springer series in statistics

  • Calabria R, Pulcini G (1997) Bayes inference for modulated power law process. Commun Stat Theory Methods 26(10):2421–2438

    MathSciNet  MATH  Google Scholar 

  • Canavos GC, Tsokos CP (1973) Bayesian estimation of life parameters in the Weibull distribution. Oper Res 21(3):755–763

    MathSciNet  MATH  Google Scholar 

  • Chen Z (2010) Empirical Bayes analysis on the power law process with natural conjugate priors. J Data Sci 8(1):139–149

    Google Scholar 

  • Dawid AP, Stone M, Zidek JV (1973) Marginalization paradoxes in Bayesian and structural inference. J R Stat Soc Ser B 35:189–233. With discussion by D. J. Bartholomew, A. D. McLaren, D. V. Lindley, Bradley Efron, J. Dickey, G. N. Wilkinson, A. P.Dempster, D. V. Hinkley, M. R. Novick, Seymour Geisser, D. A. S. Fraser and A. Zellner, and a reply by A. P. Dawid, M. Stone, and J. V. Zidek

  • Duane JT (1964) Learning curve approach to reliability monitoring. IEEE Trans Aerosp 2:563–566

    Google Scholar 

  • Eaton ML, Sudderth WD (1998) A new predictive distribution for normal multivariate linear models. Sankhyā Ser A 60(3):363–382 (Bayesian analysis)

    MathSciNet  MATH  Google Scholar 

  • Eaton ML, Sudderth WD (2004) Properties of right Haar predictive inference. Sankhyā 66(3):487–512

    MathSciNet  MATH  Google Scholar 

  • Engelhardt M, Bain L (1978) Prediction intervals for the Weibull process. Technometrics 20(2):167–169

    MATH  Google Scholar 

  • Franz J (2006) Posterior distribution and loss functions for parameter estimation in Weibull processes. Econ Qual Control 21(1):31–42

    MathSciNet  MATH  Google Scholar 

  • Franz J, Pietzner D (2012) Trend-incomplete-renewal process models for repairable systems. Econ Qual Control 27(1):65–83

    MATH  Google Scholar 

  • Franz J, Jokiel-Rokita A, Magiera R (2014) Prediction in trend-renewal processes for repairable systems. Stat Comput 24(4):633–649

    MathSciNet  MATH  Google Scholar 

  • Guida M, Calabria R, Pulcini G (1989) Bayes inference for a non-homogeneous Poisson process with power intensity law reliability. IEEE Trans Reliab 38(5):603–609

    MATH  Google Scholar 

  • Gupta PK, Singh AK (2017) Classical and Bayesian estimation of Weibull distribution in presence of outliers. Cogent Math 4:1300975

    MathSciNet  MATH  Google Scholar 

  • Guure CB, Ibrahim NA, Ahmed AM (2012) Bayesian estimation of two-parameter Weibull distribution using extension of Jeffreys’ prior information with three loss functions. Math Probl Eng 2012:589640

    MathSciNet  MATH  Google Scholar 

  • Heath D, Sudderth W (1978) On finitely additive priors, coherence, and extended admissibility. Ann Stat 6(2):333–345

    MathSciNet  MATH  Google Scholar 

  • Heath D, Sudderth W (1989) Coherent inference from improper priors and from finitely additive priors. Ann Stat 17(2):907–919

    MathSciNet  MATH  Google Scholar 

  • Hu J-M, Huang H-Z, Li Y-F, Gao H-Y (2020) Bayesian prior information fusion for power law process via evidence theory. Commun Stat Theory Methods 1–19

  • Huang Y-S, Bier VM (1998) A natural conjugate prior for the non-homogeneous Poisson process with a power law intensity function. Commun Stat Simul Comput 27(2):525–551

    MathSciNet  MATH  Google Scholar 

  • Hurtado JL, Joglar F, Mohammad M (2005) Generalized renewal process models, parameter estimation and applications to maintenance problems. Int J Perform Eng 1(1):37–50

    Google Scholar 

  • Jeffreys H (1946) An invariant form for the prior probability in estimation problems. Proc R Soc Lond Ser A 186:453–461

    MathSciNet  MATH  Google Scholar 

  • Jeffreys H (1961) Theory of probability, 3rd edn. Clarendon Press, Oxford

    MATH  Google Scholar 

  • Jokiel-Rokita A, Magiera R (2012) Estimation of parameters for trend-renewal processes. Stat Comput 22:625–637

    MathSciNet  MATH  Google Scholar 

  • Jokiel-Rokita A, Magiera R (2016) On the existence of maximum likelihood estimates in modulated gamma process. Int J Econ Stat 4:203–209

    Google Scholar 

  • Jokiel-Rokita A, Magiera R (2018) Estimation and prediction for the modulated power law process. Springer, Cham, pp 443–447

    MATH  Google Scholar 

  • Klefsö B, Kumar U (1993) Goodness-of-fit tests for the power-law process based on the ttt-plot. IEEE Trans Reliab 41(4):593–598

    Google Scholar 

  • Langberg NA, León RV, Proschan F (1980) Characterization of nonparametric classes of life distributions. Ann Probab 8(6):1163–1170

    MathSciNet  MATH  Google Scholar 

  • Lindqvist BH (1993) The trend-renewal process, a useful model for repairable systems. In: Society of reliability engineers, Scandinavian chapter, annual conference, Malmö, Sweden

  • Lindqvist BH (2006) On the statistical modeling and analysis of repairable systems. Stat Sci 21(4):532–551

    MathSciNet  MATH  Google Scholar 

  • Lindqvist BH, Doksum KA (eds) (2003) Mathematical and statistical methods in reliability, volume 7 of Series on quality, reliability and engineering statistics. World Scientific Publishing Co. Inc., River Edge. Papers from the 3rd International Conference in Mathematical Methods in Reliability held in Trondheim, June 17–20, 2002

  • Lindqvist BH, Elvebakk G, Heggland K (2003) The trend-renewal process for statistical analysis of repairable systems. Technometrics 45(1):31–44

    MathSciNet  Google Scholar 

  • Lindqvist BH, Kjønstad GA, Meland N (1994) Testing for trend in repairable system data. In: Proceedings of ESREL’94, La Boule, France

  • Pietzner D, Wienke A (2013) The trend-renewal process: a useful model for medical recurrence data. Stat Med 32(1):141–152

    MathSciNet  Google Scholar 

  • Rigdon SE, Basu AP (2000) Statistical methods for the reliability of repairable systems. Wiley, New York

    MATH  Google Scholar 

  • Ross SM (2013) Simulation, 5th edn. Elsevier/Academic Press, Amsterdam

    MATH  Google Scholar 

  • Saito Y, Dohi T (2015) Robustness of non-homogeneous gamma process-based software reliability models. In: 2015 IEEE international conference on software quality, reliability and security, pp 75–84

  • Sen A (2002) Bayesian estimation and prediction of the intensity of the power law process. J Stat Comput Simul 72(8):613–631

    MathSciNet  MATH  Google Scholar 

  • Sinha SK, Zellner A (1990) A note on the prior distributions of Weibull parameters. SCIMA 19:1–2

    MATH  Google Scholar 

  • Tang Y, Fu J, Liu W, Xu A (2017) Bayesian analysis of repairable systems with modulated power law process. Appl Math Model 44:357–373

    MathSciNet  MATH  Google Scholar 

  • Wang Y-P, Lu Z-Z (2011) Bayesian inference and prediction analysis of the power law process based on a gamma prior distribution. Commun Stat Simul Comput 40(9):1383–1401

    MathSciNet  MATH  Google Scholar 

  • Wang Y-P, Lu Z-Z (2015) Bayesian inference and prediction analysis of the power law process based on a natural conjugate prior. J Stat Comput Simul 85(5):881–898

    MathSciNet  MATH  Google Scholar 

  • Zhou H, Rigdon SE (2008) Duration dependence in US business cycles: an analysis using the modulated power law process. J Econ Finance 32:25–34

    Google Scholar 

  • Zhou H, Rigdon SE (2011) Duration dependence in bull and bear stock markets. Mod Econ 2:279–286

    Google Scholar 

Download references

Acknowledgements

We would like to thank the Referees very much for their valuable comments and suggestions.

Author information

Authors and Affiliations

  1. Wroclaw University of Science and Technology to Wrocław University of Science and Technology, Wrocław, Poland

    Alicja Jokiel-Rokita & Ryszard Magiera

Authors
  1. Alicja Jokiel-Rokita
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ryszard Magiera
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Alicja Jokiel-Rokita.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jokiel-Rokita, A., Magiera, R. Bayesian estimation versus maximum likelihood estimation in the Weibull-power law process. Comput Stat 38, 675–710 (2023). https://doi.org/10.1007/s00180-022-01241-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-022-01241-4

Keywords