Skip to main content
Springer Nature Link
Log in

Model aggregation for doubly divided data with large size and large dimension

  • Original paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

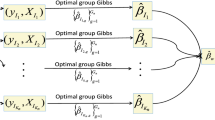
Massive data are often featured with high dimensionality as well as large sample size, which typically cannot be stored in a single machine and thus make both analysis and prediction challenging. We propose a distributed gridding model aggregation (DGMA) approach to predicting the conditional mean of a response variable, which overcomes the storage limitation of a single machine and the curse of high dimensionality. Specifically, on each local machine that stores partial data of relatively moderate sample size, we develop the model aggregation approach by splitting predictors wherein a greedy algorithm is developed. To obtain the optimal weights across all local machines, we further design a distributed and communication-efficient algorithm. Our procedure effectively distributes the workload and dramatically reduces the communication cost. Extensive numerical experiments are carried out on both simulated and real datasets to demonstrate the feasibility of the DGMA method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Ando T, Li K-C (2014) A model-averaging approach for high-dimensional regression. J Am Stat Assoc 109:254–265

    Article  MathSciNet  MATH  Google Scholar 

  • Ando T, Li K-C (2017) A weight-relaxed model averaging approach for high dimensional generalized linear models. Ann Stat 45:2645–2679

    Article  MathSciNet  Google Scholar 

  • Battey H, Fan J, Liu H, Lu J, Zhu Z (2018) Distributed testing and estimation under sparse high dimensional models. Ann Stat 46:1352–1382

    Article  MathSciNet  MATH  Google Scholar 

  • Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Trends Mach Learn 3:1–122

    MATH  Google Scholar 

  • Buckland ST, Burnham KP, Augustin NH (1997) Model selection: an integral part of inference. Biometrics 53:603–618

    Article  MATH  Google Scholar 

  • Burnham KP, Anderson DR (2003) Model selection and multimodel inference: a practical information-theoretic approach. Springer, New York

    MATH  Google Scholar 

  • Chen X, Xie M (2014) A split-and-conquer approach for analysis of extraordinarily large data. Stat Sin 24:1655–1684

    MathSciNet  MATH  Google Scholar 

  • Chen X, Zhang Y, Li R, Wu X (2016) On the feasibility of distributed kernel regression for big data. IEEE Trans Knowl Data Eng 28:3041–3052

    Article  Google Scholar 

  • Chernozhukov V, Hansen C (2004) The impact of 401(k) participation on the wealth distribution: an instrumental quantile regression analysis. Rev Econ Stat 86:735–751

    Article  Google Scholar 

  • Dai D, Rigollet P, Zhang T (2012) Deviation optimal learning using greedy Q-aggregation. Ann Stat 40:1878–1905

    Article  MathSciNet  MATH  Google Scholar 

  • Eklund J, Karlsson S (2007) Forecast combination and model averaging using predictive measures. Econ Rev 26:329–363

    Article  MathSciNet  MATH  Google Scholar 

  • Fan J, Lv J (2008) Sure independence screening for ultrahigh dimensional feature space. J R Stat Soc B 70:849–911

    Article  MathSciNet  MATH  Google Scholar 

  • Hansen BE (2007) Least squares model averaging. Econometrica 75:1175–1189

    Article  MathSciNet  MATH  Google Scholar 

  • Hansen BE, Racine JS (2012) Jackknife model averaging. J Econ 167:38–46

    Article  MathSciNet  MATH  Google Scholar 

  • Hjort NL, Claeskens G (2003) Frequentist model average estimators. J Am Stat Assoc 98:879–899

    Article  MathSciNet  MATH  Google Scholar 

  • Hoeffding W (1963) Probability inequalities for sums of bounded random variables. J Am Stat Assoc 58:13–30

    Article  MathSciNet  MATH  Google Scholar 

  • Hoeting JA, Madigan D, Raftery AE, Volinsky CT (1999) Bayesian model averaging: a turorial. Stat Sci 14:382–401

    MATH  Google Scholar 

  • Jakovetic D, Xavier J, Moura JMF (2014) Fast distributed gradient methods. IEEE Trans Autom Control 59:1131–1146

    Article  MathSciNet  MATH  Google Scholar 

  • Johnson R, Zhang T (2013) Accelerating stochastic gradient descent using predictive variance reduction. Adv Neural Inf Process Syst 26:315–323

    Google Scholar 

  • Jordan MI, Lee JD, Yang Y (2019) Communication-efficient distributed statistical learning. J Am Stat Assoc 114:668–681

    Article  MATH  Google Scholar 

  • Kleiner A, Talwalkar A, Sarkar P, Jordan MI (2014) A scalable bootstrap for massive data. J R Stat Soc B 76:795–816

    Article  MathSciNet  MATH  Google Scholar 

  • Lee JD, Liu Q, Sun Y, Taylor JE (2017) Communication-efficient sparse regression. J Mach Learn Res 18:1–30

    MathSciNet  MATH  Google Scholar 

  • Liang H, Zou G, Wan ATK, Zhang X (2011) Optimal weight choice for frequentist model average estimators. J Am Stat Assoc 106:1053–1066

    Article  MathSciNet  MATH  Google Scholar 

  • Mateos G, Bazerque JA, Giannakis GB (2010) Distributed sparse linear regression. IEEE Trans Signal Process 58:5262–5276

    Article  MathSciNet  MATH  Google Scholar 

  • Nair V, Hinton GE (2010) Rectified linear units improve restricted boltzmann machines. In: ICML’10 Proceedings of the 27th international conference on international conference on machine learning, pp 807–814

  • Newbold P, Granger CWJ (1974) Experience with forecasting univariate time series and the combination of forecast (with discussion). J R Stat Soc Ser A 137:131–165

    Article  Google Scholar 

  • Raftery AE, Madigan D, Hoeting JA (1997) Bayesian model averaging for linear regression models. J Am Stat Assoc 92:179–191

    Article  MathSciNet  MATH  Google Scholar 

  • Rosenblatt J, Nadler B (2016) On the optimality of averaging in distributed learning. Inf Inference 5:379–404

    Article  MathSciNet  MATH  Google Scholar 

  • Shamir O, Srebro N, Zhang T (2014) Communication-efficient distributed optimization using an approximate Newton-type method. Proc Int Conf Mach Learn 32:1000–1008

    Google Scholar 

  • Shang Z, Cheng G (2017) Computational limits of a distributed algorithm for smoothing spline. J Mach Learn Res 18:1–37

    MathSciNet  MATH  Google Scholar 

  • Shvachko K, Kuang H, Radia S, Chansler R (2010) The hadoop distributed file system. In: IEEE 26th symposium on mass storage systems and technologies, pp 1–10

  • van de Geer SA (2008) High-dimensional generalized linear models and the lasso. Ann Stat 36:614–645

    MathSciNet  MATH  Google Scholar 

  • Wan ATK, Zhang X, Zou G (2010) Least squares model averaging by Mallows criterion. J Econ 156:277–283

    Article  MathSciNet  MATH  Google Scholar 

  • Wang J, Kolar M, Srebro N, Zhang T (2017) Efficient distributed learning with sparsity. Proc Mach Learn Res 70:3636–3645

    Google Scholar 

  • Zaharia M, Chowdhury M, Franklin MJ, Shenker S, Stoica I (2010) Spark: cluster computing with working sets. In: Proceedings of the 2nd USENIX conference on hot topics in cloud computing, pp 10–10

  • Zhang C, Lee H, Shin K (2012) Efficient distributed linear classification algorithms via the alternating direction method of multipliers. Proc Int Conf Artif Intell Stat 22:1398–1406

    Google Scholar 

  • Zhang X, Zou G, Liang H (2014) Model averaging and weight choice in linear mixed-effects models. Biometrika 101:205–218

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang Y, Duchi J, Jordan JC, Wainwright MJ (2013) Information-theoretic lower bounds for distributed statistical estimation with communication constraints. Adv Neural Inf Process Syst 26:2328–2336

    Google Scholar 

  • Zhang Y, Duchi J, Wainwright M (2013) Divide and conquer kernel ridge regression. Conf Learn Theory 30:1–26

    MATH  Google Scholar 

  • Zhao T, Cheng G, Liu H (2016) A partially linear framework for massive heterogeneous data. Ann Stat 44:1400–1437

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank the two referees and Associate Editor for many insightful comments that greatly improved the paper. Liu’s research was partly supported by the National Natural Science Foundation of China (11971362), Yin’s research was partly supported by the Research Grants Council of Hong Kong (17308321), and Wu’s research was partly supported by the National Natural Science Foundation of China (12071483).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Wuhan University, Wuhan, Hubei, 430072, China

    Baihua He & Yanyan Liu

  2. Department of Statistics and Actuarial Science, University of Hong Kong, Pokfulam Road, Hong Kong, China

    Guosheng Yin

  3. School of Statistics and Mathematics, Zhongnan University of Economics and Law, Wuhan, Hubei, 430073, China

    Yuanshan Wu

Authors
  1. Baihua He
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yanyan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Guosheng Yin
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yuanshan Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yuanshan Wu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary Material

The supplementary material available online contains some theoretical results. (pdf 136KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

He, B., Liu, Y., Yin, G. et al. Model aggregation for doubly divided data with large size and large dimension. Comput Stat 38, 509–529 (2023). https://doi.org/10.1007/s00180-022-01242-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-022-01242-3

Keywords