Abstract
In this paper, we propose multivariate stochastic volatility models with a spherical parameterization of a Cholesky decomposition to make a time-dependent correlation matrix be positive definite without any constraints. An attractive feature of our model is that it can be easily fit using the R package NIMBLE. In addition to the spherical transformation, we introduce a multivariate L measure as a Bayesian model comparison criterion to assess the fit of different models. We present extensive simulation studies to examine the empirical performance of the proposed method and illustrate the methodology on time series of energy usage in a science building on the main campus of the University of Connecticut.Please confirm if the inserted city and country name is correct. Amend if necessary.RightPlease confirm if the corresponding author is correctly identified. Amend if necessary.Right
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Barnett G, Kohn R, Sheather S (1996) Bayesian estimation of an autoregressive model using Markov chain Monte Carlo. J Econom 74(2):237–254
Bickel PJ, Levina E (2008) Covariance regularization by thresholding. Ann Stat 2577–2604
Bollerslev T (1986) Generalized autoregressive conditional heteroskedasticity. J Econom 31(3):307–327
Chen MH, Shao QM (1999) Monte Carlo estimation of Bayesian credible and HPD intervals. J Comput Graph Stat 8(1):69–92
Chib S, Nardari F, Shephard N (2006) Analysis of high dimensional multivariate stochastic volatility models. J Econom 134(2):341–371
Chib S, Omori Y, Asai M (2009) Multivariate stochastic volatility. Handbook of financial time series. Springer, Berlin, pp 365–400
de Valpine P, Turek D, Paciorek CJ, Anderson-Bergman C, Lang DT, Bodik R (2017) Programming with models: writing statistical algorithms for general model structures with nimble. J Comput Graph Stat 26(2):403–413
Engle RF (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom J Econom Soc 987–1007
Engle RF, Kroner KF (1995) Multivariate simultaneous generalized ARCH. Econom Theory 11(1):122–150
Fox EB, Dunson DB (2015) Bayesian nonparametric covariance regression. J Mach Learn Res 16:2501–2542
Harvey A, Ruiz E, Shephard N (1994) Multivariate stochastic variance models. Rev Econ Stud 61(2):247–264
Hoff PD, Niu X (2012) A covariance regression model. Statistica Sinica 729–753
Ibrahim JG, Laud PW (1994) A predictive approach to the analysis of designed experiments. J Am Stat Assoc 89(425):309–319
Ibrahim JG, Chen MH, Sinha D (2001) Criterion-based methods for Bayesian model assessment. Statistica Sinica 419–443
Ibrahim JG, Kim S, Chen MH, Shah AK, Lin J (2019) Bayesian multivariate skew meta-regression models for individual patient data. Stat Methods Med Res 28(10–11):3415–3436
Kastner G (2016) factorstochvol: Bayesian estimation of (sparse) latent factor stochastic volatility models. R package version 08 3:908
Kastner G, Frühwirth-Schnatter S, Lopes HF (2017) Efficient Bayesian inference for multivariate factor stochastic volatility models. J Comput Graph Stat 26(4):905–917
Kim S, Shephard N, Chib S (1998) Stochastic volatility: likelihood inference and comparison with ARCH models. Rev Econ Stud 65(3):361–393
Laud PW, Ibrahim JG (1995) Predictive model selection. J Roy Stat Soc Ser B (Methodol) 57(1):247–262
Nakajima J (2017) Bayesian analysis of multivariate stochastic volatility with skew return distribution. Econom Rev 36(5):546–562
Pai JS, Ravishanker N (1996) Bayesian modelling of ARFIMA processes by Markov chain Monte Carlo methods. J Forecast 15(2):63–82
Pinheiro JC, Bates DM (1996) Unconstrained parametrizations for variance–covariance matrices. Stat Comput 6(3):289–296
Pourahmadi M (1999) Joint mean-covariance models with applications to longitudinal data: unconstrained parameterisation. Biometrika 86(3):677–690
Rambharat BR, Brockwell AE (2010) Sequential Monte Carlo pricing of American-style options under stochastic volatility models. Ann Appl Stat 222–265
Tsay RS (2005) Analysis of financial time series, vol 543. Wiley, New York
Virbickaitė A, Lopes HF, Ausín MC, Galeano P (2019) Particle learning for Bayesian semi-parametric stochastic volatility model. Econom Rev 38(9):1007–1023
Wu Y, Hernández-Lobato JM, Zoubin G (2013) Dynamic covariance models for multivariate financial time series. In: International conference on machine learning, PMLR, pp 558–566
Yu J, Meyer R (2006) Multivariate stochastic volatility models: Bayesian estimation and model comparison. Econom Rev 25(2–3):361–384
Zhang W, Leng C, Tang CY (2015) A joint modelling approach for longitudinal studies. J Roy Stat Soc Ser B (Stat Methodol) 77(1):219–238
Zou T, Lan W, Wang H, Tsai CL (2017) Covariance regression analysis. J Am Stat Assoc 112(517):266–281
Acknowledgements
We would like to thank the editor and two reviewers for their valuable comments. We thank the staff of the Department of Facilities at the University of Connecticut for providing the energy usage data. Dr. Chen’s research was partially supported by NIH Grants #GM70335 and #P01CA142538.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
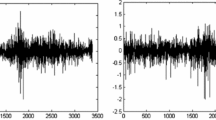
Appendix A: Trace plots for convergence diagnostics
In order to check the convergence of the MCMC algorithm, we get two random MCMC samples from a simulation replicate. The trace plots shown in Fig. 5 confirm that our proposed method has good convergence.
Trace plots for one replicate in simulation study
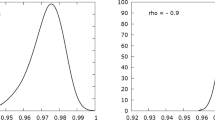
Appendix B: Marginal likelihood comparison
In order to check the performance of the marginal likelihood for model selection, we present selection results for Scenario 1 in Simulation III. We generate data from the SP-DMSV model. We fit both the SP-DMSV and FSV models, and compute the marginal likelihood under each model fit on the 2000 posterior samples. We have 100 replicates in Scenario 1. The logarithms of differences is shown in Fig. 6.
Boxplot for differences of marginal likelihood
Appendix C: Posterior estimates with credible bands
The posterior estimates with 95% credible bands for the last 50 time points are shown in Fig. 7.
Posterior estimates for last 50 time points with 95% credible bands (first row: variance (\(\sigma ^2_1.\sigma ^2_2,\sigma ^2_3\)); second row: correlation (\(\rho _{12},\rho _{13},\rho _{23}\)))
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hu, G., Chen, MH. & Ravishanker, N. Bayesian analysis of spherically parameterized dynamic multivariate stochastic volatility models. Comput Stat 38, 845–869 (2023). https://doi.org/10.1007/s00180-022-01266-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-022-01266-9