Pretest and shrinkage estimators for log-normal means

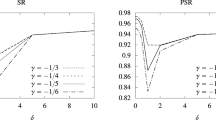
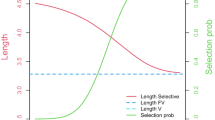
Abstract

We consider the problem of pooling means from multiple random samples from log-normal populations. Under the homogeneity assumption of means that all mean values are equal, we propose improved large sample asymptotic methods for estimating p log-normal population means when multiple samples are combined. Accordingly, we suggest estimators based on linear shrinkage, pretest, and Stein-type methodology, and consider the asymptotic properties using asymptotic distributional bias and risk expressions. We also present a simulation study to validate the performance of the suggested estimators based on the simulated relative efficiency. Historical data from finance and weather are used to in the application of the proposed estimators.

Appendices

Appendix A Proof of theorem 1

• (i) Consider $\varvec{Z}_{n}=\sqrt{{n}}\left( \hat{\varvec{\theta }}^{\mathrm{UE}}-\varvec{{\theta }} \right) \xrightarrow {D}\varvec{Z}\sim {\mathcal {N}}_{p} \left( \varvec{0}, \varvec{\Omega } \right)$ in Sect. 2. Then we can write $\varvec{U}_{n}$ as a linear function of $\varvec{Z}_{n}$ as follows:

  $\varvec{U}_{n}=\sqrt{{n}}\left( \hat{\varvec{\theta }}^{\mathrm{UE}} -{{\theta }_{0}}{\varvec{1}_{p}}\right) =\sqrt{{n}} \left( \hat{\varvec{\theta }}^{\mathrm{UE}} -\varvec{{\theta }}+\varvec{{\theta }}-{{\theta }_{0}} {\varvec{1}_{p}}\right) =\sqrt{{n}}\left( \hat{\varvec{\theta }}^{\mathrm{UE}} -\varvec{\theta }\right) +\sqrt{{n}}\left( \varvec{{\theta }}-{{\theta }_{0}} {\varvec{1}_{p}}\right) =\varvec{Z}_{n}+\varvec{h}$ . So as ${n\rightarrow \infty }$, $\varvec{U}_{n}\xrightarrow {D}\varvec{U}\sim {\mathcal {N}}_{p} \left( {{\varvec{\mu }}_{u}}, {\varvec{\Sigma }_{u}} \right)$, where ${\varvec{\mu }_{u}}=E\left[ \varvec{U}\right] =E\left[ \varvec{Z}+\varvec{h}\right] =\varvec{h}$, and ${\varvec{\Sigma }_{u}}=V\left[ \varvec{U}\right] =V\left[ \varvec{Z}+\varvec{h}\right] =\varvec{\Omega }$.

• (ii) Note that $\hat{\varvec{\theta }}^{\mathrm{RE}} ={\varvec{B}_{n}}{\hat{\varvec{\theta }}^{\mathrm{UE}}}$ and ${\varvec{B}_{n}}{{\theta }_{0}}{\varvec{1}_{p}} ={{\theta }_{0}}{\varvec{1}_{p}}$. Thus, $\varvec{W}_{n}$ can be written as a linear function of $\varvec{U}_{n}$ as follows:

  $\varvec{W}_{n}=\sqrt{{n}}\left( \hat{\varvec{\theta }}^{\mathrm{RE}}-{{\theta }_{0}}{\varvec{1}_{p}} \right) =\sqrt{{n}}\left( {\varvec{B}_{n}}{\hat{\varvec{\theta }}^{\mathrm{UE}}}-{\varvec{B}_{n}}{{\theta }_{0}}{\varvec{1}_{p}} \right) = {\varvec{B}_{n}}\sqrt{{n}}\left( {\hat{\varvec{\theta }}^{\mathrm{UE}}} -{{\theta }_{0}}{\varvec{1}_{p}} \right) ={\varvec{B}_{n}}\varvec{U}_{n}$.

  Note also that $\varvec{B}_{n}\xrightarrow {P}\varvec{B}_{0} ={{{a}}^{-1}}{\varvec{J}_{p}}{ }{\Omega }^{-1}$ is a constant matrix, where ${a}={\sum \limits _{i=1}^{p}{\tfrac{{{a}_{i}}}{{{{{\tau }}}_{i}}}}}$, and $\varvec{{\Omega }}=Diag\left( \tfrac{{{{\tau }}}_{1}}{{{a}_{1}}},...,\tfrac{{{{\tau }}}_{p}}{{{a}_{p}}} \right)$.

  If we assume $\varvec{{a}^{*}}^{\mathrm{T}}\varvec{h}=0$ where $\varvec{{a}^{*}}=\left( \tfrac{{{a}_{1}}}{{\tau }_{1}},...,\tfrac{{{a}_{p}}}{{\tau }_{p}}\right) ^{\mathrm{T}}$. Therefore, by Slutsky’s Theorem, as ${n\rightarrow \infty }$, $\varvec{W}_{n}\xrightarrow {D}\varvec{W}\sim {\mathcal {N}}_{p} \left( {\varvec{\mu }_{w}}, {\varvec{\Sigma }_{w}} \right)$, where ${\varvec{\mu }_{w}}=E\left[ \varvec{W}\right] =E\left[ \varvec{B}_{0}\varvec{U}\right] =\varvec{B}_{0}\varvec{h}=\varvec{0}$, and ${\varvec{\Sigma }_{w}}=V\left[ \varvec{W}\right] =V\left[ \varvec{B}_{0}\varvec{U}\right] =\varvec{B}_{0}\varvec{\Omega }{\varvec{B}_{0}}^{\mathrm{T}} =\varvec{\Omega }{\varvec{B}_{0}}^{\mathrm{T}} ={a}^{-1}\varvec{J}_{p}$.

• (iii) Similar to (ii), we can write $\varvec{V}_{n}$ as a linear function of $\varvec{U}_{n}$ as follows:

  $\varvec{V}_{n}=\sqrt{{n}}\left( \hat{\varvec{\theta }}^{\mathrm{UE}} -\hat{\varvec{\theta }}^{\mathrm{RE}} \right) =\sqrt{{n}} \left( \hat{\varvec{\theta }}^{\mathrm{UE}}-{{\theta }_{0}} {\varvec{1}_{p}}+{{\theta }_{0}}{\varvec{1}_{p}} -\hat{\varvec{\theta }}^{\mathrm{RE}}\right) =\sqrt{{n}} \left( \hat{\varvec{\theta }}^{\mathrm{UE}}-{{\theta }_{0}} {\varvec{1}_{p}}\right) -\sqrt{{n}}\left( \hat{\varvec{\theta }}^{\mathrm{RE}} -{{\theta }_{0}}{\varvec{1}_{p}}\right) =\varvec{U}_{n}-{\varvec{B}_{n}}\varvec{U}_{n} =\left( \varvec{I}_{p}-{\varvec{B}_{n}}\right) \varvec{U}_{n}$.

  Since $\varvec{I}_{p}-{\varvec{B}_{n}}\xrightarrow {P}\varvec{I}_{p} -{\varvec{B}_{0}}$ is a constant matrix. Thus, by Slutsky’s Theorem, as ${n\rightarrow \infty }$, $\varvec{V}_{n}\xrightarrow {D}\varvec{V}\sim {\mathcal {N}}_{p} \left( {\varvec{\mu }_{v}}, {\varvec{\Sigma }_{v}} \right)$, where ${\varvec{\mu }_{v}}=E\left[ \varvec{V}\right] =E\left[ \left( \varvec{I}_{p}-{\varvec{B}_{0}}\right) \varvec{U}\right] =\left( \varvec{I}_{p}-\varvec{B}_{0}\right) \varvec{h}=\varvec{h^{*}}$, and ${\varvec{\Sigma }_{v}} =V\left[ \varvec{V}\right] =V\left[ \left( \varvec{I}_{p} -{\varvec{B}_{0}}\right) \varvec{U}\right] =\left( \varvec{I}_{p}-{\varvec{B}_{0}}\right) \varvec{\Omega }\left( \varvec{I}_{p}-{\varvec{B}_{0}}\right) ^{\mathrm{T}} =\varvec{\Omega }\left( \varvec{I}_{p}-{\varvec{B}_{0}}\right) ^{\mathrm{T}} =\varvec{\Lambda }$.

• (iv) Now, we obtain the joint distribution of $\varvec{U}_{n}$ and $\varvec{V}_{n}$

  $\left( \begin{array}{c} {\varvec{U}_{n}} \\ {\varvec{V}_{n}} \\ \end{array}\right) =\left( \begin{array}{c} {\varvec{U}_{n}} \\ {\left( \varvec{I}_{p}-{\varvec{B}_{n}}\right) \varvec{U}_{n}} \\ \end{array}\right) =\left( \begin{array}{c} {\varvec{I}_{p}} \\ {\varvec{I}_{p}-{\varvec{B}_{n}}} \\ \end{array}\right) \varvec{U}_{n}$, which is a linear combination of $\varvec{U}_{n}$.

  So as ${n\rightarrow \infty }$, $\left( \begin{array}{c} {\varvec{U}_{n}} \\ {\varvec{V}_{n}} \\ \end{array}\right) \xrightarrow {D}\left( \begin{array}{c} {\varvec{U}} \\ {\varvec{V}} \\ \end{array}\right) \sim {\mathcal {N}}_{2p} \left( {\varvec{\mu }_{uv}}, {\varvec{\Sigma }_{uv}} \right)$, where

  ${\varvec{\mu }_{uv}}=E\left[ \left( \begin{array}{c} {\varvec{I}_{p}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) \varvec{U}_{n}\right] =\left( \begin{array}{c} {\varvec{I}_{p}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) E\left[ \varvec{U}_{n}\right] =\left( \begin{array}{c} {\varvec{I}_{p}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) \varvec{h}=\left( \begin{array}{c} {\varvec{h}} \\ {\varvec{h}^{*}} \\ \end{array}\right)$, and

  ${\varvec{\Sigma }_{uv}}=V\left[ \left( \begin{array}{c} {\varvec{I}_{p}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) \varvec{U}_{n}\right] =\left( \begin{array}{c} {\varvec{I}_{p}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) V\left[ \varvec{U}_{n}\right] \left( \begin{array}{cc} {\varvec{I}_{p}} &{}\left( {\varvec{I}_{p} -{\varvec{B}_{0}}}\right) ^{\mathrm{T}} \\ \end{array}\right) =\left( \begin{array}{cc} {\varvec{\Omega }} &{}\varvec{\Omega }\left( {\varvec{I}_{p} -{\varvec{B}_{0}}}\right) ^{\mathrm{T}} \\ \left( {\varvec{I}_{p}-{\varvec{B}_{0}}}\right) \varvec{\Omega } &{}\left( {\varvec{I}_{p} -{\varvec{B}_{0}}}\right) \varvec{\Omega } \left( {\varvec{I}_{p}-{\varvec{B}_{0}}}\right) ^{\mathrm{T}}\\ \end{array}\right) =\left( \begin{array}{cc} {\varvec{\Omega }} &{}\varvec{\Lambda } \\ \varvec{\Lambda }^{\mathrm{T}} &{}\varvec{\Lambda } \\ \end{array}\right)$.

• (v) Similar to (iv), we write $\left( \begin{array}{c} {\varvec{W}_{n}} \\ {\varvec{V}_{n}} \\ \end{array} \right) =\left( \begin{array}{c} {\varvec{B}_{n}} {\varvec{U}_{n}} \\ \left( \varvec{I}_{p}-{\varvec{B}_{n}}\right) \varvec{U}_{n}\\ \end{array} \right) =\left( \begin{array}{c} {\varvec{B}_{n}} \\ \varvec{I}_{p}-{\varvec{B}_{n}}\\ \end{array} \right) {\varvec{U}_{n}}$, which is also a linear combination of ${\varvec{U}_{n}}$.

  As ${n\rightarrow \infty }$, we have $\left( \begin{array}{c} {\varvec{W}_{n}} \\ {\varvec{V}_{n}} \\ \end{array}\right) \xrightarrow {D}\left( \begin{array}{c} {\varvec{W}} \\ {\varvec{V}} \\ \end{array}\right) \sim {\mathcal {N}}_{2p} \left( {\varvec{\mu }_{wv}}, {\varvec{\Sigma }_{wv}} \right)$, where

  ${\varvec{\mu }_{wv}}=E\left[ \left( \begin{array}{c} {\varvec{B}_{0}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) \varvec{U}_{n}\right] =\left( \begin{array}{c} {\varvec{B}_{0}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) E\left[ \varvec{U}_{n}\right] =\left( \begin{array}{c} {\varvec{B}_{0}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) \varvec{h}=\left( \begin{array}{c} {\varvec{B}_{0}}{\varvec{h}} \\ \left( {\varvec{I}_{p}-{\varvec{B}_{0}}}\right) {\varvec{h}} \\ \end{array}\right) =\left( \begin{array}{c} \varvec{0} \\ {\varvec{h}}^{*} \\ \end{array}\right)$, and

  ${\varvec{\Sigma }_{wv}}=V\left[ \left( \begin{array}{c} {\varvec{B}_{0}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) \varvec{U}_{n}\right] =\left( \begin{array}{c} {\varvec{B}_{0}} \\ {\varvec{I}_{p}-{\varvec{B}_{0}}} \\ \end{array}\right) V\left[ \varvec{U}_{n}\right] \left( \begin{array}{cc} {\varvec{B}_{0}^{\mathrm{T}}} &{}\left( {\varvec{I}_{p} -{\varvec{B}_{0}}}\right) ^{\mathrm{T}} \\ \end{array}\right) =\left( \begin{array}{cc} {\varvec{B}_{0}}{\varvec{\Omega }}{\varvec{B}_{0}^{\mathrm{T}}} &{} {\varvec{B}_{0}}\varvec{\Omega }\left( {\varvec{I}_{p} -{\varvec{B}_{0}}}\right) ^{T} \\ \left( {\varvec{I}_{p}-{\varvec{B}_{0}}}\right) \varvec{\Omega }{\varvec{B}_{0}^{\mathrm{T}}} &{} \left( {\varvec{I}_{p}-{\varvec{B}_{0}}}\right) \varvec{\Omega }\left( {\varvec{I}_{p} -{\varvec{B}_{0}}}\right) ^{\mathrm{T}} \\ \end{array}\right) =\left( \begin{array}{cc} {a}^{-1}\varvec{J}_{p} &{}\varvec{0} \\ \varvec{0} &{}\varvec{\Lambda } \\ \end{array}\right)$.

  Note that $\left( {\varvec{I}_{p}-{\varvec{B}_{0}}}\right) \varvec{\Omega }{\varvec{B}_{0}^{\mathrm{T}}} =\varvec{\Omega }{\varvec{B}_{0}^{\mathrm{T}}} -{\varvec{B}_{0}}\varvec{\Omega }{\varvec{B}_{0}^{\mathrm{T}}} =\varvec{\Omega }{\varvec{B}_{0}^{\mathrm{T}}} -\varvec{\Omega }{\varvec{B}_{0}^{\mathrm{T}}}=\varvec{0}$.

Appendix B Proof of theorem 2

• (i) $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{UE}}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{UE}}}-\varvec{\theta }_{(n)} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}}\right\} =\varvec{0}$.

• (ii) $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{RE}}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{RE}}}-\varvec{\theta }_{(n)} \right) \right\} = \underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{RE}}}-\hat{\varvec{\theta }}^{\mathrm{UE}}+\hat{\varvec{\theta }}^{\mathrm{UE}}-\varvec{\theta }_{(n)} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ -\varvec{V}_{n}\right\} =-\varvec{h}^{*}$.

• (iii) $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{SE}}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{SE}}}-\varvec{\theta }_{(n)} \right) \right\} = \underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( k \hat{\varvec{\theta }}^{\mathrm{RE}} +\left( 1-k\right) \hat{\varvec{\theta }}^{\mathrm{UE}}-\varvec{\theta }_{(n)}\right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{UE}}}-\varvec{\theta }_{(n)} \right) -k\sqrt{n}\left( \hat{\varvec{\theta }}^{\mathrm{UE}}-\hat{\varvec{\theta }}^{\mathrm{RE}} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}}-k{\varvec{V}_{n}}\right\} =-k\varvec{h}^{*}$.

• (iv) $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{P}}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{P}}}-\varvec{\theta }_{(n)} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}} -({{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}}-{{{\hat{\varvec{\theta }}}^{\mathrm{RE}}}}) I({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}})-\varvec{\theta }_{(n)}\right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{UE}}}-\varvec{\theta }_{(n)} \right) -\sqrt{n}\left( ({{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}}-{{{\hat{\varvec{\theta }}}^{\mathrm{RE}}}}) I({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}}) \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E \left\{ {\varvec{Z}_{n}}-{\varvec{V}_{n}}I ({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}})\right\} =-E\left\{ \varvec{V} I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right\}$.

  By considering Lemma 2 (i), we write

  $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{P}}}\right) =-\mu _{\varvec{v}} {E}\left\{ I(\chi _{p+1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right\} =-\varvec{h}^{*}G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right)$.

• (v) Similar to (iv).

• (vi) $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}}}-\varvec{\theta }_{(n)} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}} -(p-3){\mathcal {T}}_{n}^{-1}({{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}}-{{{\hat{\varvec{\theta }}}^{\mathrm{RE}}}})-\varvec{\theta }_{(n)} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E \left\{ {\varvec{Z}_{n}}-(p-3){\varvec{V}_{n}} {\mathcal {T}}_{n}^{-1}\right\} =-(p-3)E\left\{ \varvec{V} \chi _{p-1}^{-2}(\Theta )\right\} =-(p-3)\varvec{h}^{*}E\left\{ \chi _{p+1}^{-2}(\Theta )\right\}$.

• (vii) $\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}+}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}+}}-\varvec{\theta }_{(n)} \right) \right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( {{{\hat{\varvec{\theta }}}^{\mathrm{JS}}}} -\{1-(p-3){\mathcal {T}}_{n}^{-1}\}I({\mathcal {T}}_{n}<p-3)({{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}}-{{{\hat{\varvec{\theta }}}^{\mathrm{RE}}}})-\varvec{\theta }_{(n)} \right) \right\} =\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}}}\right) -\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \sqrt{n}\left( ({{{\hat{\varvec{\theta }}}^{\mathrm{UE}}}}-{{{\hat{\varvec{\theta }}}^{\mathrm{RE}}}})\{1-(p-3){\mathcal {T}}_{n}^{-1}\}I({\mathcal {T}}_{n}<p-3)\right) \right\} =\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}}}\right) -\underset{n\rightarrow \infty }{\mathop {\lim }}\,E \left\{ {\varvec{V}_{n}}I({\mathcal {T}}_{n}<p-3)\right\} +\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ (p-3) {\varvec{V}_{n}}{\mathcal {T}}_{n}^{-1}I({\mathcal {T}}_{n}<p-3) \right\} =\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}}}\right) -E\left\{ {\varvec{V}} I(\chi _{p-1 }^{2}(\Theta )<p-3)\right\} +(p-3)E\left\{ \varvec{V} \chi _{p-1}^{-2}(\Theta )I(\chi _{p-1 }^{2}(\Theta )<p-3) \right\} =\mathbf {B}\left( {\hat{\varvec{\theta } }^{\mathrm{JS}}}\right) -\varvec{h}^{*}G_{p+1}(p-3 ; \Theta )+(p-3)\varvec{h}^{*}E\left\{ \chi _{p+1}^{-2}(\Theta )I(\chi _{p+1 }^{2}(\Theta )<p-3)\right\} =-\varvec{h}^{*}\left\{ G_{p+1}(p-3 ; \Theta )+(p-3) {E}\left[ \chi _{p+1}^{-2}(\Theta ) I\left( \chi _{p+1}^{2}(\Theta )>(p-3)\right) \right] \right\}$.

The quadratic bias expressions in Theorem 2 can be obtained by using these results along with Eq. 17.

Appendix C Proof of theorem 3

• (i) $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{UE}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ n\left( {\hat{\varvec{\theta } }}^{\mathrm{UE}}-\varvec{\theta }_{(n)} \right) {{\left( {\hat{\varvec{\theta } }}^{\mathrm{UE}}-\varvec{\theta }_{(n)} \right) }^{\mathrm{T}}}\right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}}{\varvec{Z}_{n}}^{\mathrm{T}}\right\} =E\left\{ {\varvec{Z}}{\varvec{Z}}^{\mathrm{T}}\right\} =V\left\{ {\varvec{Z}}\right\} =\varvec{\Omega }$.

• (ii) We can write $\sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{RE}}}-\varvec{\theta }_{(n)} \right) =\sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{RE}}} -{{\theta }_{0}}{\varvec{1}_{p}}+{{\theta }_{0}} {\varvec{1}_{p}}-\varvec{\theta }_{(n)}\right) =\varvec{W}_{n}-\varvec{h}$, which is a linear function of $\varvec{W}_{n}$. By Slutsky’s Theorem, as ${n\rightarrow \infty }$, $\sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{RE}}}-\varvec{\theta }_{(n)} \right) \xrightarrow {D}{\mathcal {N}}_{p} \left( {-\varvec{h}^{*}}, {a}^{-1}\varvec{J}_{p}\right)$. Thus,

  $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{RE}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ n\left( {\hat{\varvec{\theta } }}^{\mathrm{RE}}-\varvec{\theta }_{(n)} \right) {{\left( {\hat{\varvec{\theta } }}^{\mathrm{RE}}-\varvec{\theta }_{(n)} \right) }^{\mathrm{T}}}\right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ (\varvec{W}_{n} -\varvec{h})(\varvec{W}_{n}-\varvec{h})^{\mathrm{T}}\right\} =E\left\{ (\varvec{W}-\varvec{h})(\varvec{W} -\varvec{h})^{\mathrm{T}}\right\} = V\left\{ \varvec{W} -\varvec{h}\right\} +E\left\{ \varvec{W}-\varvec{h}\right\} E\left\{ \varvec{W}-\varvec{h}\right\} ^{\mathrm{T}} ={a}^{-1} \varvec{J}_{p}+\varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}$.

• (iii) We can write $\sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{SE}}}-\varvec{\theta }_{(n)} \right) ={\varvec{Z}_{n}}-k{\varvec{V}_{n}}={\varvec{Z}_{n}} -k({\varvec{I}_{p}}-{\varvec{B}_{n}}){\varvec{U}_{n}} ={\varvec{Z}_{n}}-k({\varvec{I}_{p}}-{\varvec{B}_{n}}) (\varvec{Z}_{n}+\varvec{h}) =\left[ {\varvec{I}_{p}}-k({\varvec{I}_{p}} -{\varvec{B}_{n}})\right] {\varvec{Z}_{n}} -k({\varvec{I}_{p}}-{\varvec{B}_{n}})\varvec{h}$, which is a linear function of $\varvec{Z}_{n}$. By Slutsky’s Theorem, as ${n\rightarrow \infty }$, $\sqrt{n}\left( {\hat{\varvec{\theta } }^{\mathrm{SE}}} -\varvec{\theta }_{(n)} \right) \xrightarrow {D}{\mathcal {N}}_{p} \left( {-k\varvec{h}^{*}}, \left[ {\varvec{I}_{p}} -k({\varvec{I}_{p}}-{\varvec{B}_{0}})\right] {\varvec{\Omega }}\left[ {\varvec{I}_{p}} -k({\varvec{I}_{p}}-{\varvec{B}_{0}})\right] ^{\mathrm{T}}\right)$. Thus,

  $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{SE}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E \left\{ n\left( {\hat{\varvec{\theta } }}^{\mathrm{SE}} -\varvec{\theta }_{(n)} \right) {{\left( {\hat{\varvec{\theta } }}^{\mathrm{SE}} -\varvec{\theta }_{(n)} \right) }^{\mathrm{T}}}\right\} =\left[ {\varvec{I}_{p}}-k({\varvec{I}_{p}} -{\varvec{B}_{0}})\right] {\varvec{\Omega }} \left[ {\varvec{I}_{p}}-k({\varvec{I}_{p}} -{\varvec{B}_{0}})\right] ^{\mathrm{T}}+k^{2}\varvec{h^{*}} \varvec{h^{*}}^{\mathrm{T}}$.

• (iv) $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{P}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E \left\{ n\left( {\hat{\varvec{\theta } }}^{\mathrm{P}} -\varvec{\theta }_{(n)} \right) {{\left( {\hat{\varvec{\theta } }}^{\mathrm{P}} -\varvec{\theta }_{(n)} \right) }^{\mathrm{T}}}\right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \left[ {\varvec{Z}_{n}} -{\varvec{V}_{n}}I({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}})\right] \left[ {\varvec{Z}_{n}}-{\varvec{V}_{n}}I({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}})\right] ^{\mathrm{T}}\right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}} {\varvec{Z}_{n}}^{\mathrm{T}} \right\} -2\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}}{\varvec{V}_{n}}^{\mathrm{T}} I({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}})\right\} + \underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{V}_{n}} {\varvec{V}_{n}}^{\mathrm{T}}I({\mathcal {T}}_{n}<{{{\mathcal {T}}_{\alpha }}})\right\} = V\left\{ {\varvec{Z}}\right\} - 2E\left\{ {\varvec{Z}}{\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right\} +E\left\{ {\varvec{V}}{\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right\}$.

  By Lemma 2 (ii), we write

  $E\left\{ {\varvec{V}}{\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right\} =\varvec{\Lambda }G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right) + \varvec{h^{*}}\varvec{h^{*}}^{T}G_{p+3}\left( \chi _{p-1,\alpha }^{2};\Theta \right)$.

  Now, by using the law of iterated expectations and Lemma 2 (i) and (ii), we write

  $E\left\{ {\varvec{Z}}{\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right\} =E\left[ E\left\{ {\varvec{Z}}{\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\mid {\varvec{V}}\right\} \right] =E\left[ E\left( {\varvec{Z}}\mid {\varvec{V}}\right) {\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right] =E\left[ {\varvec{V}}{\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right] -\varvec{h^{*}}E\left[ {\varvec{V}^{\mathrm{T}}}I(\chi _{p-1 }^{2}(\Theta )<\chi _{p-1,\alpha }^{2})\right] =\varvec{\Lambda }G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right) + \varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}G_{p+3}\left( \chi _{p-1,\alpha }^{2};\Theta \right) -\varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right)$. Therefore,

  $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{P}}\right) =\varvec{\Omega }-\varvec{\Lambda }G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right) -\varvec{h^{*}} \varvec{h^{*}}^{\mathrm{T}}G_{p+3}\left( \chi _{p-1,\alpha }^{2};\Theta \right) +2\varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right) = \varvec{\Omega }-\varvec{\Lambda }G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right) + \varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}} \left[ 2G_{p+1}\left( \chi _{p-1,\alpha }^{2};\Theta \right) -G_{p+3} \left( \chi _{p-1,\alpha }^{2};\Theta \right) \right]$.

• (v) Similar to (iv).

• (vi) $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{JS}}\right) =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ n\left( {\hat{\varvec{\theta } }}^{\mathrm{JS}}-\varvec{\theta }_{(n)} \right) {{\left( {\hat{\varvec{\theta } }}^{\mathrm{JS}}-\varvec{\theta }_{(n)} \right) }^{\mathrm{T}}}\right\} =\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ \left[ {\varvec{Z}_{n}}-(p-3){\varvec{V}_{n}}{\mathcal {T}}_{n}^{-1}\right] \left[ {\varvec{Z}_{n}}-(p-3){\varvec{V}_{n}}{\mathcal {T}}_{n}^{-1}\right] ^{\mathrm{T}}\right\} = \underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}}{\varvec{Z}_{n}}^{\mathrm{T}}\right\} -2(p-3)\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{Z}_{n}}{\varvec{V}_{n}}^{\mathrm{T}}{\mathcal {T}}_{n}^{-1}\right\} + (p-3)^{2}\underset{n\rightarrow \infty }{\mathop {\lim }}\,E\left\{ {\varvec{V}_{n}}{\varvec{V}_{n}}^{\mathrm{T}}{\mathcal {T}}_{n}^{-2}\right\} = E\left\{ {\varvec{Z}}{\varvec{Z}}^{\mathrm{T}}\right\} -2(p-3)E\left\{ {\varvec{Z}}{\varvec{V}}^{\mathrm{T}}\chi _{p-1}^{-2}(\Theta )\right\} +(p-3)^{2}E \left\{ {\varvec{V}}{\varvec{V}}^{\mathrm{T}} \chi _{p-1}^{-4}(\Theta )\right\}$.

  Now,

  $E\left\{ {\varvec{Z}}{\varvec{V}}^{\mathrm{T}}\chi _{p-1}^{-2}(\Theta )\right\} =E\left\{ E\left( {\varvec{Z}}{\varvec{V}}^{\mathrm{T}}\chi _{p-1}^{-2}(\Theta )\mid {\varvec{V}}\right) \right\} = E\left\{ E\left( {\varvec{Z}}\mid {\varvec{V}}\right) {\varvec{V}}^{\mathrm{T}}\chi _{p-1}^{-2}(\Theta )\right\} =E\left\{ {\varvec{V}}{\varvec{V}^{\mathrm{T}}}\chi _{p-1}^{-2} (\Theta )\right\} -\varvec{h^{*}}E\left\{ {\varvec{V}^{\mathrm{T}}} \chi _{p-1}^{-2}(\Theta )\right\} =\varvec{\Lambda }E \left\{ \chi _{p+1}^{-2}(\Theta )\right\} +\varvec{h^{*}} \varvec{h^{*}}^{\mathrm{T}}E\left\{ \chi _{p+3}^{-2}(\Theta )\right\} -\varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}E \left\{ \chi _{p+1}^{-2}(\Theta )\right\}$.

  Note that $E\left\{ \chi _{p+3}^{-2}(\Theta )\right\} =E\left\{ \chi _{p+1}^{-2}(\Theta )\right\} -2E\left\{ \chi _{p+3}^{-4}(\Theta )\right\}$ (See Saleh (2006) page 33). Thus,

  $E\left\{ {\varvec{Z}}{\varvec{V}}^{\mathrm{T}}\chi _{p-1}^{-2} (\Theta )\right\} =\varvec{\Lambda }E\left\{ \chi _{p+1}^{-2}(\Theta ) \right\} -2\varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}E \left\{ \chi _{p+3}^{-4}(\Theta )\right\}$. By Lemma 2 (ii), we write

  $E\left\{ {\varvec{V}}{\varvec{V}}^{\mathrm{T}}\chi _{p-1}^{-4}(\Theta )\right\} =\varvec{\Lambda }E\left\{ \chi _{p+1}^{-4}(\Theta )\right\} +\varvec{h^{*}} \varvec{h^{*}}^{\mathrm{T}}E\left\{ \chi _{p+3}^{-4}(\Theta )\right\}$.Therefore,

  $\mathrm{M}\left( {\hat{\varvec{\theta } }}^{\mathrm{JS}}\right) =\varvec{\Omega } -2(p-3)\left( \varvec{\Lambda }E \left\{ \chi _{p+1}^{-2}(\Theta )\right\} -2\varvec{h^{*}}\varvec{h^{*}}^{\mathrm{T}}E\left\{ \chi _{p+3}^{-4} (\Theta )\right\} \right) +(p-3)^{2}\left( \varvec{\Lambda }E \left\{ \chi _{p+1}^{-4}(\Theta )\right\} +\varvec{h^{*}} \varvec{h^{*}}^{\mathrm{T}}E\left\{ \chi _{p+3}^{-4}(\Theta )\right\} \right) = \varvec{\Omega }-(p-3)\varvec{\Lambda }\left( 2E \left\{ \chi _{p+1}^{-2}(\Theta )\right\} -(p-3)E\left\{ \chi _{p+1}^{-4} (\Theta )\right\} \right) + (p-3)(p+1)\varvec{h^{*}} \varvec{h^{*}}^{\mathrm{T}}E\left\{ \chi _{p+3}^{-4}(\Theta )\right\}$.

• (vii) Similar to (vi).

The risk expressions in Theorem 3 can be obtained by using these results along with Eq. 19.