Deep support vector quantile regression with non-crossing constraints

Abstract

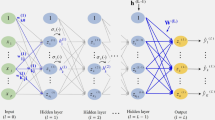
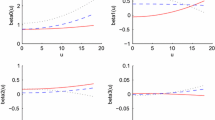
We propose a new nonparametric regression approach that combines deep neural networks with support vector quantile regression models. The nature of deep neural networks enables complex nonlinear regression quantiles to be estimated more accurately. Because deep learning models have a complicated structure, the proposed method can easily fit both smooth and non-smooth data sets. For this reason, we can effectively model data sets with truncated points or locally different smoothness in which spline-based smoothing methods often fail. Stepwise fitting is used to increase computing speed when fitting multiple quantiles. This produces stable fits, especially when observations are scarce near the target quantile. In addition, we employ certain constraints to prevent the fitted quantiles from crossing. The benefits of the proposed method are more apparent when the errors are heteroscedastic, although quantile regression does not require homogeneous errors. We illustrate the flexibility of the proposed method using simulated data sets and six real data examples with univariate and multivariate input variables.