Skip to main content
SpringerLink
Log in

Bandwidth selection for local linear regression: A simulation study

  • Published:
Computational Statistics Aims and scope Submit manuscript

An Erratum to this article was published on 01 July 2000

This article has been updated

Summary

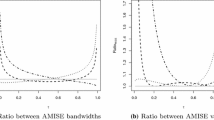
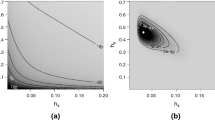
This paper provides a simulation study of several popular bandwidth selectors for local linear regression. The study also includes two new selectors which couple the non-asymptotic plug-in and the unbiased risk estimation techniques. These two new selectors are simple to describe, easy to implement and performed very well in our simulation study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8

Similar content being viewed by others

Change history

  • 11 September 2000

    Due to a mix up a few lines of authors’ working notes were included in the article (page 530). These lines should be ignored and the remainder of the article is the correct final version.

References

  • Chiu, S.-T. (1991), ‘Some stabilized bandwidth selectors for nonparametric regression’, The Annals of Statistics 19, 1528–1546.

    Article  MathSciNet  Google Scholar 

  • Chiu, S.-T. (1992), ‘An automatic bandwidth selector for kernel density estimation’, Biometrika 79, 771–782.

    Article  MathSciNet  Google Scholar 

  • Chiu, S.-T. (1996), ‘A comparative review of bandwidth selection for kernel density estimation’, Statistica Sinica 6, 129–145.

    MathSciNet  MATH  Google Scholar 

  • Efron, B. & Tibshirani, R. J. (1993), An Introduction to the Bootstrap, Chapman and Hall, New York.

    Book  Google Scholar 

  • Fan, J. & Gijbels, I. (1995), ‘Data-driven bandwidth selection in local polynomial fitting: variable bandwidth and spatial adaptation’, Journal of the Royal Statistical Society Series B 57, 371–394.

    MathSciNet  MATH  Google Scholar 

  • Fan, J. & Gijbels, I. (1996), Local Polynomial Modelling and Its Applications, Chapman and Hall, London.

    MATH  Google Scholar 

  • Gasser, T. & Müller, H. G. (1984), ‘Estimating regression functions and their derivatives by the kernel method’, Scandinavian Journal of Statistics 11, 171–185.

    MathSciNet  MATH  Google Scholar 

  • Gasser, T., Kneip, A. & Köhler, W. (1991), ‘A flexible and fast method for automatic smoothing’, Journal of the American Statistical Association 86, 643–652.

    Article  MathSciNet  Google Scholar 

  • Hall, P. & Turlach, B. A. (1997), ‘Interpolation methods for adapting to sparse design in nonparametric regression’, Journal of the American Statistical Association 92, 466–476.

    Article  MathSciNet  Google Scholar 

  • Hall, P., Marron, J. S. & Park, B. U. (1992), ‘Smoothed cross-validation’, Probability Theory and Related Fields 92, 1–20.

    Article  MathSciNet  Google Scholar 

  • Hastie, T. & Loader, C. (1993), ‘Local regression: automatic kernel carpentry (with discussion)’, Statistical Sciences 8, 120–143.

    Article  Google Scholar 

  • Härdle, W., Hall, P. & Marron, J. S. (1992), ‘Regression smoothing parameters that are not far from their optimum’, Journal of the American Statistical Association 87, 227–233.

    MathSciNet  MATH  Google Scholar 

  • Jones, M. C. (1991), ‘The roles of ISE and MISE in density estimation’, Statistics and Probability Letters 12, 51–56.

    Article  MathSciNet  Google Scholar 

  • Ruppert, D., Sheather, S. J. & Wand, M. P. (1995), ‘An effective bandwidth selector for local least squares regression’, Journal of the American Statistical Association 90, 1257–1270.

    Article  MathSciNet  Google Scholar 

  • Wand, M. & Gutierrez, R. G. (1997), ‘Exact risk approaches to smoothing parameter selection’, Journal of Nonparametric Statistics 8, 337–354.

    Article  MathSciNet  Google Scholar 

  • Wand, M. P. & Jones, M. C. (1995), Kernel Smoothing, Chapman and Hall, London.

    Book  Google Scholar 

Download references

Acknowledgment

Most of the work was done while the first author was with the Department of Statistics, Macquarie University. The authors thank Steve Marron, three anonymous referees and an associate editor for many helpful comments, and Matt Wand for providing a preprint of Wand & Gutierrez (1997). The work was partially supported by an Australian Research Council grant. This document was prepared using computer facilities supported in part by National Science Foundation Grant DMS 89-05292 awarded to the Department of Statistics at The University of Chicago, and by The University of Chicago Block Fund.

Author information

Authors and Affiliations

  1. Department of Statistics, The University of Chicago, 5734 S. University Avenue, Chicago, Illinois, 60637, USA

    Thomas C. M. Lee

  2. Department of Statistics, Macquarie University, Sydney, NSW, 2109, Australia

    Victor Solo

Authors
  1. Thomas C. M. Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Victor Solo
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lee, T.C.M., Solo, V. Bandwidth selection for local linear regression: A simulation study. Computational Statistics 14, 515–532 (1999). https://doi.org/10.1007/s001800050029

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s001800050029

Keywords

Search

Navigation