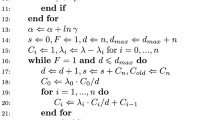Summary
The likelihood function of a continuous-discrete state space model is computed recursively by Monte Carlo integration, using importance sampling techniques. A functional integral representation of the transition density is utilized and importance densities are obtained by smoothing. Examples are the likelihood surfaces of an AR(2) process, a Ginzburg-Landau model and stock price models with stochastic volatilities.















Similar content being viewed by others
References
Alspach, D. & Sorenson, H. (1972), ‘Nonlinear Bayesian estimation using Gaussian sum approximations’, IEEE Transactions on Automatic Control 17, 439–448.
Anderson, B. & Moore, J. (1979), Optimal Filtering, Prentice Hall, Englewood Cliffs.
Apple Computer (2001), Macintosh Programmer’s Workshop, http://-developer.apple.com/tools/mpw-tools/.
Arnold, L. (1974), Stochastic Differential Equations, John Wiley, New York.
Arnold, V. (1973), Ordinary Differential Equations, MIT Press, Cambridge (Mass.), London.
Arnold, V. (1986), Catastrophy Theory, Springer, Berlin.
Bergstrom, A. (1990), Continuous Time Econometric Modelling, Oxford University Press, Oxford.
Carlin, B., Poison, N. & Stoffer, D. (1992), ‘A Monte Carlo Approach to Non-normal and Nonlinear State-Space Modeling’, Journal of the American Statistical Association 87, 493–500.
Durbin, J. & Koopman, S. (1997), ‘Monte Carlo maximum likelihood estimation for non-Gaussian state space models’, Biometrika 84,3, 669–684.
Durbin, J. & Koopman, S. (2000), ‘Time series analysis of non-Gaussian observations based on state space models from both classical and Bayesian perspectives.’, Journal of the Royal Statistical Association B 62, 1, 3–56.
Engle, R. & Bollerslev, L. (1986), ‘Modelling the persistence of conditional variances’, Econometric Reviews 5, 1–50.
Fahrmeir, L. & Kaufmann, H. (1991), ‘On Kalman Filtering, Posterior Mode Estimation and Fisher Scoring in Dynamic Exponential Family Regression’, Metrika 38, 37–60.
Frey, M. (1996), ‘A Wiener Filter, State-Space Flux-Optimal Control Against Escape from a Potential Well’, IEEE Transactions on Automatic Control 41, 2, 216–223.
Gelb, A., ed. (1974), Applied Optimal Estimation, MIT Press, Cambridge, Mass.
Gordon, N., Salmond, D. & Smith, A. (1993), ‘Novel approach to nonlinear/non-Gaussian Bayesian state estimation’, IEEE Transactions on Radar and Signal Procesing 140, 2, 107–113.
Haken, H. (1977), Synergetics, Springer, Berlin.
Hammersley, J. & Handscomb, D. (1964), Monte Carlo Methods, Methuen, London.
Harvey, A. (1989), Forecasting, structural time series models and the Kalman filter, Cambridge University Press, Cambridge.
Harvey, A. & Stock, J. (1985), ‘The estimation of higher order continuous time autoregressive models’, Econometric Theory 1, 97–112.
Herings, J. (1996), Static and Dynamic Aspects of General Disequilibrium Theory, Kluwer, Boston, London, Dordrecht.
Holmes, P. J. (1981), ‘Center manifolds, normal forms and bifurcations of vector fields’, Physica D 2, 449–481.
Hull, J. & White, A. (1987), ‘The Pricing of Options with Stochastic Volatilities’, Journal of Finance XLII,2, 281–300.
Hürzeler, M. & Künsch, H. (1998), ‘Monte Carlo Approximations for General State-Space Models’, Journal of Computational and Graphical Statistics 7,2, 175–193.
Jazwinski, A. (1970), Stochastic Processes and Filtering Theory, Academic Press, New York.
Jones, R. (1984), Fitting multivariate models to unequally spaced data, in E. Parzen, ed., ‘Time Series Analysis of Irregularly Observed Data’, Springer, New York, pp. 158–188.
Jones, R. & Ackerson, L. (1990), ‘Serial correlation in unequally spaced longitudinal data’, Biometrika 77, 721–731.
Jones, R. & Tryon, P. (1987), ‘Continuous time series models for unequally spaced data applied to modeling atomic clocks’, SIAM J. Sci. Stat. Comput. 8, 71–81.
Kim, S., Shephard, N. & Chib, S. (1998), ‘Stochastic Volatility: Likelihood Inference and Comparision with ARCH Models’, Review of Economic Studies 45, 361–393.
Kitagawa, G. (1987), ‘Non-Gaussian state space modeling of nonstationary time series’, Journal of the American Statistical Association 82, 1032–1063.
Kitagawa, G. (1996), ‘Monte Carlo Filter and Smoother for Non-Gaussian Nonlinear State Space Models’, Journal of Computational and Graphical Statistics 5,1, 1–25.
Kloeden, P. & Platen, E. (1992), Numerical Solution of Stochastic Differential Equations, Springer, Berlin.
Liptser, R. & Shiryayev, A. (1977, 1978), Statistics of Random Processes, Volumes I and II, Springer, New York, Heidelberg, Berlin.
Lo, A. (1988), ‘Maximum Likelihood Estimation of Generalized Itô Processes with Discretely Sampled Data’, Econometric Theory 4, 231–247.
Nelson, D. (1990), ‘ARCH models a diffusion approximations’, Journal of Econometrics 45, 7–38.
Nelson, D. (1992), ‘Filtering and forecasting with misspecified ARCH models I’, Journal of Econometrics 52, 61–90.
Press, W., Teukolsky, S., Vetterling, W. & Flannery, B. (1992), Numerical Recipes in C, second edn, Cambridge University Press, Cambridge.
Risken, H. (1989), The Fokker-Planck Equation, second edn, Springer, Berlin, Heidelberg, New York.
Scott, L. (1987), ‘Option pricing when the variance changes randomly: Theory, estimation, and an application’, Journal of Financial and Quantitative Analysis 22, 419–438.
Shoji, I. & Ozaki, T. (1997), ‘Comparative Study of Estimation Methods for Continuous Time Stochastic Processes’, Journal of Time Series Analysis 18, 5, 485–506.
Shoji, I. & Ozaki, T. (1998), ‘A statistical method of estimation and simulation for systems of stochastic differential equations’, Biometrika 85, 1, 240–243.
Silverman, B. (1986), Density estimation for statistics and data analysis, Chapman and Hall, London.
Singer, H. (1993b), ‘Continuous-time dynamical systems with sampled data, errors of measurement and unobserved components’, Journal of Time Series Analysis 14, 5, 527–545.
Singer, H. (1995), ‘Analytical score function for irregularly sampled continuous time stochastic processes with control variables and missing values’, Econometric Theory 11, 721–735.
Singer, H. (1997a), Nonlinear Continuous-Discrete Filtering and ML Estimation using Kernel Density Estimates and Functional Integrals, Regensburger Beiträge zur Statistik und Ökonometrie 40, Universität Regensburg.
Singer, H. (1999b), Parameter Estimation of Nonlinear Stochastic Differential Equations: Simulated Maximum Likelihood vs. Extended Kalman Filter and Itô-Taylor Expansion, Regensburger Beiträge zur Statistik und Ökonometrie 41, Universität Regensburg.
Stratonovich, R. (1989), Some Markov methods in the theory of stochastic processes in nonlinear dynamic systems, in F. Moss & P. McClintock, eds, ‘Noise in nonlinear dynamic systems’, Cambridge University Press, pp. 16–71.
Tanizaki, H. (1996), Nonlinear filters: estimation and applications, second edn, Springer, Berlin.
Tanizaki, H. & Mariano, R. (1995), Prediction, Filtering and Smoothing in Nonlinear and Non-normal Cases using Monte-Carlo Integration, in H. Van Dijk, A. Monfort & B. Brown, eds, ‘Econometric Inference using Simulation Techniques’, John Wiley, pp. 245–261.
Wagner, W. (1988), ‘Monte Carlo Evaluation of Functionals of Solutions of Stochastic Differential Equations. Variance Reduction and Numerical Examples’, Stochastic Analysis and Applications 6, 447–468.
Wiggins, J. (1987), ‘Option values under stochastic volatility’, Journal of Financial Economics 19, 351–372.
Wolfram, S. (1992), Mathematica, 2nd edn, Addison-Wesley, Redwood City.
Wong, E. & Hajek, B. (1985), Stochastic Processes in Engineering Systems, Springer, New York.
Zadrozny, P. (1988), ‘Gaussian likelihood of continuous-time armax models when data are stocks and flows at different frequencies’, Econometric Theory 4, 108–124.
Author information
Authors and Affiliations
Appendix
Appendix
In this appendix it is shown, that the EKF update of the a priori density (21) leads to the correct variance reduced Monte Carlo estimator of the likelihood
Using the Bayes formula this can be rewritten as
where dη = dηJi−1 … dη0 and for this the optimal variance reducing density is
Therefore the optimal estimator is
which is the same as inserting (21) into (62). It. remains to note that
since
Rights and permissions
About this article
Cite this article
Singer, H. Simulated Maximum Likelihood in Nonlinear Continuous-Discrete State Space Models: Importance Sampling by Approximate Smoothing. Computational Statistics 18, 79–106 (2003). https://doi.org/10.1007/s001800300133
Published:
Issue Date:
DOI: https://doi.org/10.1007/s001800300133