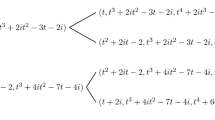Abstract
For any positive integer parameters a and b, Gurvich recently introduced a generalization mex b of the standard minimum excludant mex = mex1, along with a game NIM(a, b) that extends further Fraenkel’s NIM = NIM(a, 1), which in its turn is a generalization of the classical Wythoff NIM = NIM(1, 1). It was shown that P-positions (the kernel) of NIM(a, b) are given by the following recursion:
and conjectured that for all a, b the limits ℓ(a, b) = x n (a, b)/n exist and are irrational algebraic numbers. In this paper we prove that showing that \({\ell(a,b) = \frac{a}{r-1}}\), where r > 1 is the Perron root of the polynomial
whenever a and b are coprime; furthermore, it is known that ℓ(ka, kb) = kℓ(a, b). In particular, \({\ell(a, 1) = \alpha_a = \frac{1}{2} (2 - a + \sqrt{a^2 + 4})}\). In 1982, Fraenkel introduced the game NIM(a) = NIM(a, 1), obtained the above recursion and solved it explicitly getting \({x_n = \lfloor \alpha_a n \rfloor, \; y_n = x_n + an = \lfloor (\alpha_a + a) n \rfloor}\). Here we provide a polynomial time algorithm based on the Perron–Frobenius theory solving game NIM(a, b), although we have no explicit formula for its kernel.
Similar content being viewed by others
References
Berlekamp ER, Conway JH, Guy RK (2001–2004) Winning ways for your mathematical plays, vols 1–4, 2nd edn. Peters AK, Natick
Conway JH (1976) On numbers and games. Academic Press, London
Coxeter HSM (1953) The golden section, Phyllotaxis and Wythoff’s game. Scr Math 19: 135–143
Fraenkel AS (1982) How to beat your Wythoff games’ opponent on three fronts. Am Math Monthly 89: 353–361
Fraenkel AS (1984) Wythoff games, continued fractions, cedar trees and Fibonacci searches. Theor Comput Sci 29: 49–73
Fraenkel AS (2004) Complexity, appeal, and challenges of combinatorial games. Theor Comput Sci 313: 393–415
Fraenkel AS, Peled U (2013) Harnessing the unwieldy MEX function. Preprint. To appear in Games of No Chance 4. http://www.wisdom.weizmann.ac.il/~fraenkel/Papers/Harnessing.The.Unwieldy.MEX.Function_2.pdf
Gurvich V (2010) A four parametric generalization of the Wythoff NIM and its recursive solution. RUTCOR Research Report 18-2010, Rutgers University
Gurvich V (2011) Miserable and strongly miserable impartial games, RUTCOR Research Report 18-2011, Rutgers University
Gurvich V (2012) Further generalizations of the Wythoff game and the minimum excludant, RUTCOR Research Report 16-2010, Rutgers University. Discr Appl Math 160: 941–947
Hadad U (2008) Polynomializing seemingly hard sequences using surrogate sequences. MS. Thesis, Faculty of Mathematics, Weizmann Institute of Science
Larsson U (2006) Permutations of the natural numbers with prescribed difference multisets. Integers 6: A3
Larsson U (2009a) 2-pile Nim with a restricted number of move-size dynamic imitations. Integers 9: G4
Larsson U (2009b) Restrictions of m-Wythoff Nim and p-complementary Beatty sequences, In: Albert M, Nowakowski R (eds) Games of no chance, vol 3. MSRI 56, Cambridge University Press, Cambridge
Larsson U (2009c) Sequences and games generalizing the combinatorial game of Wythoff NIM. PhD Thesis, Götheborg University
Meyer CD (2000) Matrix analysis and applied linear algebra, SIAM, Philadelphia
Prasolov VV (2010) Polynomials. In: Algorithms and computation in mathematics, vol 11. Springer, Berlin
Wythoff WA (1907) A modification of the game of Nim. Nieuw Archief voor Wiskunde 7: 199–202
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Boros, E., Gurvich, V. & Oudalov, V. A polynomial algorithm for a two parameter extension of Wythoff NIM based on the Perron–Frobenius theory. Int J Game Theory 42, 891–915 (2013). https://doi.org/10.1007/s00182-012-0338-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-012-0338-6
Keywords
- Combinatorial and impartial games
- NIM
- Wythoff’s NIM
- Fraenkel’s NIM
- Minimum excludant
- Algebraic number
- Asymptotic
- Kernel