Abstract
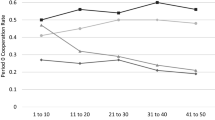
Cooperation in prisoner’s dilemma games can usually be sustained only if the game has an infinite horizon. We analyze to what extent the theoretically crucial distinction of finite versus infinite-horizon games is reflected in the outcomes of a prisoner’s dilemma experiment. We compare three different experimental termination rules in four treatments: a known finite end, an unknown end, and two variants with a random termination rule (with a high and with a low continuation probability, where cooperation can occur in a subgame-perfect equilibrium only with the high probability). We find that the termination rules do not significantly affect average cooperation rates. Specifically, employing a random termination rule does not cause significantly more cooperation compared to a known finite horizon, and the continuation probability does not significantly affect average cooperation rates either. However, the termination rules may influence cooperation over time and end-game behavior. Further, the (expected) length of the game significantly increases cooperation rates. The results suggest that subjects may need at least some learning opportunities (like repetitions of the supergame) before significant backward induction arguments in finitely repeated game have force.
Similar content being viewed by others
References
Andreoni J, Miller JH (1993) Rational cooperation in the finitely repeated prisoners’ dilemma: experimental evidence. Econ J 103: 570–585
Angelova V, Bruttel LV, Güth W, Kamecke U (2011) Can subgame perfect equilibrium threats foster cooperation? An experimental test of finite-horizon folk theorems. Econ Inq (forthcoming)
Axelrod R (1984) The evolution of cooperation. Basic Books, New York
Axelrod R (1980) More effective choice in the prisoner’s dilemma. J Confl Resolut 24: 379–403
Benoit J-P, Krishna V (1985) Finitely repeated games. Econometrica 53(4): 905–922
Benoit J-P, Krishna V (1987) Nash equilibria of finitely repeated games. Int J Game Theory 16(3): 197–204
Bolton GE, Ockenfels A (2000) ERC: a theory of equity, reciprocity and competition. Am Econ Rev 90: 166–193
Bruttel L, Kamecke U (2012) Infinity in the lab. How do people play repeated games? Theory Dec 72(2): 205–219
Bruttel LV, Güth W, Kamecke U (2012) Finitely repeated prisoners’ dilemma experiments without a commonly known end. Int J Game Theory 41(1): 23–47
Dal Bo P (2005) Cooperation under the shadow of the future: experimental evidence from infinitely repeated games. Am Econ Rev 95: 1591–1604
Engle-Warnick J, Slonim RL (2004) The evolution of strategies in a repeated trust game. J Econ Behav Organ 55: 553–573
Fehr E, Schmidt KM (1999) A theory of fairness, competition and cooperation. Q J Econ 114: 817–868
Feinberg RM, Husted TA (1993) An experimental test of discount effects on collusive behavior in dupoly markets. J Ind Econ 41(2): 153–160
Fischbacher U (2007) Z-Tree, Zurich toolbox for readymade economic experiments. Exp Econ 10(2): 171–178
Flood MM (1952) Some experimental games. Research Memorandum RM-789. RAND Corporation, Santa Monica, CA
Fouraker L, Siegel S (1963) Bargaining behavior. McGraw-Hill, New York
Gonzales LG, Güth W, Levati V (2005) When does the game end? Public goods experiments with non-definite and non-commonly known time horizons. Econ Lett 88(2): 221–226
Hollander M, Wolfe DA (1999) Nonparametric statistical methods. Wiley, New York
Holt CH (1985) An experimental test of the consistent—conjectures hypothesis. Am Econ Rev 75: 314–325
Kaplan T, Ruffle B (2006) Which way to cooperate? Working Paper, Ben-Gurion University
Kreps DM, Milgrom P, Roberts J, Wilson R (1982) Rational cooperation in the finitely repeated prisoner’s dilemma. J Econ Theory 27(2): 245–252
Luce RD, Raiffa H (1957) Games and decisions: introduction and critical survey. Wiley, New York
Morehous LG (1966) One-play, two-play, five-play, and ten-play runs of prisoner’s dilemma. J Confl Resolut 10: 354–361
Murnighan JK, Roth AE (1983) Expecting continued play in prisoner’s dilemma games: a test of three models. J Confl Resolut 27: 279–300
Neyman A (1999) Cooperation in repeated games when the number of stages is not commonly known econometrica. Econometrica 67: 45–64
Orzen H (2008) Counterintuitive number effects in experimental oligopolies. Exp Econ 11(4): 390–401
Rapoport A, Cammah AM (1965) Prisoner’s dilemma. A study in conflict and cooperation. University of Michigan Press, Ann Arbor
Roth AE (1995) Bargaining experiments. In: Kagel J, Roth AE (eds) Handbook of experimental economics. Princeton University Press, Princeton, pp 253–348
Roth AE, Murnighan JK (1978) Equilibrium behavior and repeated play of the prisoners’ dilemma. J Math Psychol 17: 189–198
Samuelson L (1987) A note on uncertainty and cooperation in a finitely repeated prisoner’s dilemma. International Journal of Game Theory 16(3): 187–195
Selten R, Stoecker R (1986) End behavior in finite prisoner’s dilemma supergames. J Econ Behav Organ 7: 47–70
Selten R, Mitzkewitz M, Uhlich GR (1997) Duopoly strategies programmed by experienced players. Econometrica 65: 517–556
Suetens S, Potters J (2007) Bertrand Colludes more than Cournot. Exp Econ 10(1): 71–77
Stahl DO (1991) The graph of prisoner’s dilemma supergame payoffs as a function of the discount factor. Games Econ Behav 3: 360–384
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Normann, HT., Wallace, B. The impact of the termination rule on cooperation in a prisoner’s dilemma experiment. Int J Game Theory 41, 707–718 (2012). https://doi.org/10.1007/s00182-012-0341-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-012-0341-y