Wythoff partizan subtraction

Abstract

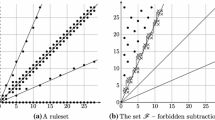
We introduce a class of normal-play partizan games, called Complementary Subtraction. These games are instances of Partizan Subtraction where we take any set A of positive integers to be Left’s subtraction set and let its complement be Right’s subtraction set. In wythoff partizan subtraction we take the set A and its complement B from wythoff nim, as the two subtraction sets. As a function of the heap size, the maximum size of the canonical forms grows quickly. However, the value of the heap is either a number or, in reduced canonical form, a switch. We find the switches by using properties of the Fibonacci word and standard Fibonacci representations of integers. Moreover, these switches are invariant under shifts by certain Fibonacci numbers. The values that are numbers, however, are distinct, and we can find their binary representation in polynomial time using a representation of integers as sums of Fibonacci numbers, known as the ternary (or “the even”) Fibonacci representation.

Appendix: Combinatorial game theory background

We give a very brief overview of normal-play combinatorial games (Albert et al. 2007; Berlekamp et al. 2001; Siegel 2013), followed by some background on the reduced canonical form (Siegel 2013).

In a combinatorial game, there is a given starting position, two players move alternately, and the game finishes after a finite sequence of moves (regardless of the order of play). Moreover, there is perfect information, and there is no chance device. A player who cannot move loses.

The two players are called Left and Right. By the Fundamental Theorem of Combinatorial Games (Albert et al. 2007, Theorem 2.1) each game belongs to exactly one of four outcome classes:

• ${\mathcal {L}}$: (Left wins) Left can force a win regardless of moving first or second;

• ${\mathcal {R}}$: (Right wins) Right can force a win regardless of moving first or second;

• $\mathcal {N}$: (Next player wins) the current player can force a win (regardless of whether it is Left or Right to play);

• $\mathcal {P}$: (Previous player wins) the current player cannot force a win (regardless of whether it is Left or Right to play).

The set of Left (Right) options of a game G contains those games that Left (Right) can move to in one move, this set is denoted $G^{\mathcal {L}}$ ($G^{\mathcal {R}}$). We identify G with its sets of options and write $G := \{ G^{\mathcal {L}}\mid G^{\mathcal {R}}\}$. In the case where $G^{\mathcal {L}}=G^{\mathcal {R}}=\emptyset$, we denote G by 0; i.e. $0 = \{\emptyset \mid \emptyset \}$.

The disjunctive sum of two games, G and H, is a game $G+H$, in which a player plays in either G or H. Its recursive definition is $G + H := \{ G^{\mathcal {L}}+H, G+H^{\mathcal {L}}\mid G^{\mathcal {R}}+H, G+H^{\mathcal {R}}\}$, where e.g. $G^{\mathcal {L}} + H := \{G^{L} + H \mid G^L\in G^{\mathcal {L}}\}$, if $G^{\mathcal {L}}\ne \emptyset$, and otherwise $G^{\mathcal {L}} + H := \emptyset$. With the disjunctive sum as the binary operation, equivalence classes of games form a partially ordered abelian group, where the equivalence is given by $G=H$ if $G-H\in \mathcal {P}$ if and only if $G-H=0$. Here, $G - H := G + (-H)$, where $- H := \{ -H^{\mathcal {R}}\mid -H^{\mathcal {L}}\}$ is the negative of H. Moreover, the partial order is given by $G > H$ if $G-H\in {\mathcal {L}}$ (or equivalently $H-G\in {\mathcal {R}}$), and so G is incomparable to H if and only if $G-H\in \mathcal {N}$. With these definitions, Left prefers the games which are greater in the order, whereas Right prefers the lesser ones.

Knowing the outcome class of both G and H is not sufficient to determine the outcome class of $G+H$. A refinement is required. The canonical form of a position is obtained by eliminating dominated options and bypassing reversible options (similar to t. The canonical form can sometimes be interpreted as the ‘number of moves advantage’ for Left. For example, $\{ \mid \} = 0$, since neither player has a move, and $\{0\mid \} = 1$, since this is the position in which Left has one move and Right none. Similarly, $\{ \mid 0\} = -1$, a one move advantage to Right.

In more generality, a game is a number if every option is to a game which is worse than the original game for that player.

Definition 2

The position G is a number if, for all $G^L$, $G^L - G < 0$ and, for all $G^R$, $G^R - G > 0$.

The Simplicity Theorem (Siegel 2013, Theorem 3.10, page 72) is restated here, only for the numbers we see in this paper.

Theorem 12

(Simplicity Theorem) Let $G=\{G^L\mid G^R\}$, where $G^L$ and $G^R$ numbers in the interval $0\leqslant G^L<G^R\leqslant 1$. Then G is the simplest number strictly between its options, i.e. $G = a/2^b$, where b is the smallest integer such that $G^L<a/2^b <G^R$, for an odd number a. Moreover, the number a is unique.

Inductively, all numbers in this interval are dyadic rationals with odd numerators; a is unique because if we had two such odd numerators a, then an even numerator between them would result in a simplified number with a smaller denominator. There are many applications of this idea in this paper, beginning with Proposition 1; later, we apply the binary representation of numbers.

The stops are the best numbers that a player can obtain under alternating play.

Definition 3

The Left stop and Right stop of G, written L(G) and R(G) respectively, are given by

$$\begin{aligned} L(G) ={\left\{ \begin{array}{ll} G, \text{ if } G \text{ is } \text{ a } \text{ number; }\\ \max \limits _{G^L\in G^{\mathcal {L}}}\{R(G^L)\}, \text{ o.w.; } \end{array}\right. }\\ R(G) ={\left\{ \begin{array}{ll} G, \text{ if } G \text{ is } \text{ a } \text{ number; }\\ \min \limits _{G^R\in G^{\mathcal {R}}}\{L(G^R)\}, \text{ o.w. } \end{array}\right. } \end{aligned}$$

A position G is hot if $L(G)>R(G)$, and infinitesimal if $L(G)=R(G)=0$.

1.1 Reduced canonical form

The reduced canonical form is introduced in Calistrate (1996), however, the proof was flawed and a corrected version appears in Grossman and Siegel (2009). It is a relatively new tool, but shows its importance in Nowakowski and Ottaway (2011), McKay et al. (2015), Mesdal (2009). The following development is taken from Siegel (2013). Two games, G and H are infinitesimally close if $-x< G-H < x$ for all positive numbers x. We write this as $G=_{\inf } H$. This is the equivalence relation modulo infinitesimals. For games G and H, $G\geqslant _{\inf } H$ if $G-H\geqslant -x$ for all positive numbers x. Note that the relation $\geqslant _{\inf }$ is a partial order; this is the partial order modulo infinitesimals.

Definition 4

(inf-reduction) Let G be a game.

• 1. A Left option $G^{L_1}$ is inf-dominated by $G^{L_2}$, if $G^{L_2}\geqslant _{\inf } G^{L_1}$.

• 2. A Right option $G^{R_1}$ is inf-dominated by $G^{R_2}$, if $G^{R_1}\geqslant _{\inf } G^{R_2}$.

• 3. A Left option $G^{L_1}$ is inf-reversible (through $G^{L_1R_1}$), if $G\geqslant _{\inf } G^{L_1R_1}$ for some Right option $G^{L_1R_1}$.

• 4. A Right option $G^{R_1}$ is inf-reversible (through $G^{R_1L_1}$), if $G^{R_1L_1}\geqslant _{\inf } G$ for some Left option $G^{R_1L_1}$.

Theorem 13

(Siegel 2013) Assume that G is not equal to a number and suppose that $G'$ is obtained by removing some inf-dominated option (either Left or Right). Then $G=_{\inf } G'$.

Lemma 29

(Siegel 2013) Let G be a game and suppose that $G^{L_1}$ is inf-reversible through $G^{L_1R_1}$. Let

$$\begin{aligned} G' = \{G^{L_1R_1L},G^{L'}\mid G^{\mathcal {R}}\}, \end{aligned}$$

where $G^{L_1R_1L}$ ranges over all Left options of $G^{L_1R_1}$ and $G^{L'}$ ranges over all Left options of G except $G^{L_1}$. If $G'$ is not a number, then $G=_{\inf }G'$.

Theorem 14

(Siegel 2013) Assume that G is hot and suppose that some Left option $G^{L_1}$ is inf-reversible through $G^{L_1R_1}$. Let $G'$ be as in Lemma 29. Then $G=_{\inf }G'$.

A position H is a sub-position of a position G if there is a (not necessarily alternating and possibly empty) sequence of consecutive moves from G to H.

Definition 5

A position K is in reduced canonical form, if, for every sub-position H of K, either H is in canonical form and is a number, or H is hot and H does not contain any inf-dominated or inf-reversible options.

The next result is a combination of results in Siegel (2013).

Theorem 15

For every game G, there exists a unique position K in reduced canonical form such that $G=_{\inf } K$.

Definition 6

The reduced canonical form of a game G, denoted $\mathrm{rcf}({G})$, is the unique reduced canonical form K, such that $\mathrm{rcf}({G}) = K$.

The next result simplifies game comparison modulo infinitesimals, since showing $G\geqslant _{\inf } K$ is equivalent to showing $G-K\geqslant _{\inf }0$.

Theorem 16

The following are equivalent.

• 1. $R(G)\geqslant 0$;

• 2. $G\geqslant _{\inf } 0$;

• 3. $G\geqslant \epsilon$ for some infinitesimal $\epsilon$.

Observe that the first item is often most convenient to use in proofs.