Entry with two correlated signals: the case of industrial espionage and its positive competitive effects

Abstract

Recent advances in information and communication technologies have increased the incentives for firms to acquire information about rivals. These advances may have major implications for market entry because they make it easier for potential entrants to gather valuable information about, for example, an incumbent’s cost structure. However, little theoretical research has actually analyzed this question. This paper advances the literature by extending a one-sided asymmetric information version of Milgrom and Roberts’ (1982) limit pricing model. Here, the entrant is allowed access to an intelligence system (IS) of a certain precision that generates a noisy signal on the incumbent’s cost structure. The entrant thus decides whether to enter the market based on two signals: the price charged by the incumbent and the signal sent by the IS. Crucially, for intermediate values of IS precision, the set of pooling equilibria with ex-ante profitable market entry is non-empty. Moreover, the probability of ex-ante non-profitable entry is strictly positive. In classical limit pricing models, an entrant never enters in a pooling equilibrium, so this result suggests that the use of an IS may potentially increase competition.

Appendix

Proof of Lemma 1

(i)

$$\Pi_{L} \left( p \right) - \Pi_{H} \left( p \right) = C_{H} \left( {Q\left( p \right)} \right) - C_{L} \left( {Q\left( p \right)} \right)$$

$$\frac{\partial }{\partial p}\left[ {\Pi_{L} \left( p \right) - \Pi_{H} \left( p \right)} \right] = Q^{\prime}\left( p \right)\left[ {C^{\prime}_{H} \left( {Q\left( p \right)} \right) - C^{\prime}_{L} \left( {Q\left( p \right)} \right)} \right]$$

By Assumptions 4 and 5, the right-hand side of the above expression is negative.

(ii)

$$\begin{gathered} p_{L}^{M} q_{L}^{M} - C_{L} \left( {q_{L}^{M} } \right) \ge p_{H}^{M} q_{H}^{M} - C_{L} \left( {q_{H}^{M} } \right) \hfill \\ p_{H}^{M} q_{H}^{M} - C_{H} \left( {q_{H}^{M} } \right) \ge p_{L}^{M} q_{L}^{M} - C_{H} \left( {q_{L}^{M} } \right) \hfill \\ \end{gathered}$$

Adding the two inequalities gives

$$C_{H} \left( {q_{L}^{M} } \right) - C_{L} \left( {q_{L}^{M} } \right) \ge C_{H} \left( {q_{H}^{M} } \right) - C_{L} \left( {q_{H}^{M} } \right)$$

By Assumption 4, we have that $q_{L}^{M} \ge q_{H}^{M}$ and hence $p_{L}^{M} \le p_{H}^{M}$.

Let us show that $p_{L}^{M} < p_{H}^{M}$. If not, then $p_{L}^{M} = p_{H}^{M}$. Since the first-order condition (FOC) for M of type $t$ is

$$\frac{{\partial \Pi_{t} }}{\partial p}\left( {Q\left( p \right)} \right) = 0 \leftrightarrow C^{\prime}_{t} \left( {Q\left( p \right)} \right) = p + \frac{Q\left( p \right)}{{Q^{\prime}\left( p \right)}}$$

the solution does not depend on $t$, namely $C^{\prime}_{L} \left( {Q\left( {p_{L}^{M} } \right)} \right) = C^{\prime}_{H} \left( {Q\left( {p_{L}^{M} } \right)} \right)$. However, this contradicts Assumption 4.

(iii) By Assumption 3,

$$\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$$

Note that $D_{L} = \prod_{L} \left( {p_{0} } \right)$ and $D_{H} = \prod_{H} \left( {\hat{p}} \right)$. Hence, this inequality can be written as

$$\Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{L} \left( {p_{0} } \right) > \Pi_{H} \left( {p_{H}^{M} } \right) - \Pi_{H} \left( {\hat{p}} \right)$$

Thus,

$$\Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{L}^{M} } \right) + \underbrace {{\Pi_{H} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{H}^{M} } \right)}}_{ < 0} > \Pi_{L} \left( {p_{0} } \right) - \Pi_{H} \left( {\hat{p}} \right)$$

Hence,

$$\Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{L}^{M} } \right) > \Pi_{L} \left( {p_{0} } \right) - \Pi_{H} \left( {\hat{p}} \right)$$

(A1)

Since $p_{0} \le p_{L}^{M}$, we have by section (i) of Lemma 1

$$\Pi_{L} \left( {p_{0} } \right) - \Pi_{H} \left( {p_{0} } \right) > \Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{L}^{M} } \right)$$

Together with (A1), this implies that

$$\Pi_{H} \left( {\hat{p}} \right) > \Pi_{H} \left( {p_{0} } \right)$$

But $p_{0} < p_{H}^{M}$ and $\hat{p} < p_{H}^{M}$ and by Assumption 2 $p_{0} < \hat{p}$.

Proof of Lemma 2

(i) By (3) in the main text,

$$Prob_{n} \left( {H\left| {h,p} \right.} \right) = \frac{{\mu \alpha \frac{{f_{n} \left( {p\left| H \right.} \right)}}{{f_{n} \left( {p\left| L \right.} \right)}}}}{{\mu \alpha \frac{{f_{n} \left( {p\left| H \right.} \right)}}{{f_{n} \left( {p\left| L \right.} \right)}} + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}$$

Hence,

$$Prob\left( {H\left| {h,p} \right.} \right) = \frac{\mu \alpha g\left( p \right)}{{\mu \alpha g\left( p \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}$$

(A2)

and by Assumption 7, $Prob\left( {H\left| {h,p} \right.} \right)$ is continuous in $p$.

The proof that $Prob\left( {H\left| {l,p} \right.} \right)$ is continuous is similarly derived from (4) in the main text.

Since $Prob\left( {L\left| {s,p} \right.} \right) = 1 - Prob\left( {H\left| {s,p} \right.} \right)$, then $Prob\left( {L\left| {s,p} \right.} \right)$ is also continuous.

Next, note that $g\left( p \right)$ is non-decreasing in $p$ since $g_{n} \left( p \right)$ is increasing in $p$ for all $n$. Therefore, Theorem 1 in Milgrom (1981) implies that if $p_{1} > p_{2}$, the posterior $Prob\left( {H\left| {s,p_{1} } \right.} \right)$ dominates $Prob\left( {H\left| {s,p_{2} } \right.} \right)$, $s = \left\{ {h,l} \right\}$, in the sense of first-order stochastic dominance. In fact, it is easy to verify by (A2) that $\frac{\partial }{\partial p}Prob\left( {H\left| {h,p} \right.} \right) \ge 0$ if and only if $g^{\prime}\left( p \right) \ge 0$ and thus $Prob\left( {H\left| {h,p} \right.} \right)$ is non-decreasing in $p$. The proof that $Prob\left( {H\left| {l,p} \right.} \right)$ is non-decreasing is similar.

(ii) Let

$$x_{n} \left( p \right) = \frac{{Prob_{n} \left( {H\left| {h,p} \right.} \right)}}{{Prob_{n} \left( {H\left| {l,p} \right.} \right)}}$$

By (3) and (4) in the main text,

$$\begin{gathered} x_{n} \left( p \right) - 1 = \frac{{\frac{\alpha }{1 - \alpha }\left[ {\mu \left( {1 - \alpha } \right)f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\alpha f_{n} \left( {p\left| L \right.} \right)} \right]}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} - 1 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {1 - \mu } \right)\frac{{\alpha^{2} }}{1 - \alpha }f_{n} \left( {p\left| L \right.} \right) - \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {1 - \mu } \right)f_{n} \left( {p\left| L \right.} \right)\left( {2\alpha - 1} \right)}}{{\left( {1 - \alpha } \right)\left[ {\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)} \right]}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {1 - \mu } \right)\left( {2\alpha - 1} \right)}}{{\left( {1 - \alpha } \right)\left[ {\mu \alpha g_{n} \left( p \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)} \right]}} \hfill \\ \end{gathered}$$

Hence,

$$\mathop {\lim }\limits_{n \to \infty } \left[ {x_{n} \left( p \right) - 1} \right] = \frac{{\left( {1 - \mu } \right)\left( {2\alpha - 1} \right)}}{{\left( {1 - \alpha } \right)\left[ {\mu \alpha g\left( p \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)} \right]}}\, > 0$$

Hence $\mathop {\lim }\limits_{n \to \infty } x_{n} \left( p \right)\, > 1$ and, consequently, for every $p \ge 0$,

$$Prob\left( {H\left| {h,p} \right.} \right) > Prob\left( {H\left| {l,p} \right.} \right)$$

Proof of Lemma 3. By (5) in the main text,

$$\begin{gathered} \Pi_{E} \left( {s,p} \right) = Prob\left( {H\left| {s,p} \right.} \right)\Delta_{E} \left( H \right) + Prob\left( {L\left| {s,p} \right.} \right)\Delta_{E} \left( L \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = Prob\left( {L\left| {s,p} \right.} \right)\left[ {\frac{{Prob\left( {H\left| {s,p} \right.} \right)}}{{Prob\left( {L\left| {s,p} \right.} \right)}}\Delta_{E} \left( H \right) + \Delta_{E} \left( L \right)} \right] \hfill \\ \end{gathered}$$

(A3)

Let $s = h$. For every $p$,

$$\frac{{Prob\left( {H\left| {h,p} \right.} \right)}}{{Prob\left( {L\left| {h,p} \right.} \right)}} = \mathop {\lim }\limits_{n \to \infty } \frac{{\mu \alpha f_{n} \left( {p\left| H \right.} \right)}}{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} = \frac{\mu \alpha }{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}g\left( p \right)$$

We claim that $g\left( p \right) \to 0$ as $p \to 0$. This follows from Dini’s theorem, as $g_{n} \left( p \right)$ is increasing in $n$, $g_{n} \left( p \right)$ is continuous in $p$, and $g\left( p \right)$ is also continuous. Hence, for every $\gamma > 0$, $\mathop {\lim }\limits_{n \to \infty } g_{n} \left( p \right) = g\left( p \right)$ uniformly on $\left[ {0,\gamma } \right]$. Since, for every $n$, $g_{n} \left( p \right) \to 0$ as $p \to 0$, we have $g\left( p \right) \to 0$ as $p \to 0$. Consequently,

$\mathop {\lim }\limits_{p} \frac{{Prob\left( {H\left| {h,p} \right.} \right)}}{{Prob\left( {L\left| {h,p} \right.} \right)}} = 0$, as $p \to 0$ (A4).

Inequality (A4) also holds when $h$ is replaced by $l$ (the proof is similar).

Next, let us show that $Prob\left( {L\left| {h,p} \right.} \right) > 0$ for small $p$.

$$\begin{gathered} Prob_{n} \left( {L\left| {h,p} \right.} \right) = \frac{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{1 + \frac{{\mu \alpha g_{n} \left( p \right)}}{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}}} \hfill \\ \end{gathered}$$

(A5)

Again, since $g_{n} \left( p \right) \to g\left( p \right)$ as $n \to \infty$ uniformly in any interval $\left[ {0,\gamma } \right]$, $\gamma > 0$, and since $g\left( p \right) \to 0$ as $p \to 0$,

$Prob\left( {L\left| {h,p} \right.} \right) = \mathop {\lim }\limits_{n} Prob_{n} \left( {L\left| {h,p} \right.} \right) \to 1$, as $p \to 0$.

In particular, $Prob\left( {L\left| {h,p} \right.} \right) > 0$ for $p$ sufficiently small. Similarly, we can prove that $Prob\left( {L\left| {l,p} \right.} \right) > 0$ for $p$ sufficiently small.

Now, (A3), (A4), and the fact that $\Delta_{E} \left( L \right) < 0$ and $Prob\left( {L\left| {s,p} \right.} \right) > 0$ for small $p$, imply that for sufficiently small $p$, $\Pi_{E} \left( {s,p} \right) < 0$ and $J_{s} \ne \emptyset$.

Let us show that for $p$ sufficiently large, $\Pi_{E} \left( {s,p} \right) > 0$. We use the following claim.

Claim 1. $\mathop {\lim }\limits_{p} Prob\left( {L\left| {s,p} \right.} \right) = 0$ as $p \to \infty$.

Proof: Let $n = 1$ and $s = h$. By Assumption 7.2, $\lim \frac{{f_{1} \left( {p\left| H \right.} \right)}}{{f_{1} \left( {p\left| L \right.} \right)}} = \infty$. By (A5),

$Prob_{1} \left( {L\left| {h,p} \right.} \right) \to 0$ as $p \to \infty$.

Hence, for every $\varepsilon > 0$, there exists $P$ such that for all $p > P$,

$$Prob_{1} \left( {L\left| {h,p} \right.} \right) < \varepsilon$$

By (3) in the main text,

$$Prob_{n} \left( {H\left| {h,p} \right.} \right) = \frac{\mu \alpha }{{\mu \alpha + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)\frac{{f_{n} \left( {p\left| L \right.} \right)}}{{f_{n} \left( {p\left| H \right.} \right)}}}}$$

By Assumption 7.2, $Prob_{n} \left( {H\left| {h,p} \right.} \right)$ is increasing in $n$ and, hence, $Prob_{n} \left( {L\left| {h,p} \right.} \right)$ is decreasing in $n$ for every $p$. Thus, for all $p > P$,

$$Prob_{n} \left( {L\left| {h,p} \right.} \right) < Prob_{1} \left( {L\left| {h,p} \right.} \right) < \varepsilon$$

Hence, for every $\varepsilon > 0$ and for all $p > P$,

$$Prob\left( {L\left| {h,p} \right.} \right) = \mathop {\lim }\limits_{n \to \infty } Prob_{n} \left( {L\left| {h,p} \right.} \right) \le \varepsilon$$

implying that

$$\mathop {\lim }\limits_{p \to \infty } Prob\left( {L\left| {h,p} \right.} \right) = 0$$

The proof that $\mathop {Prob}\limits_{p} \left( {L\left| {l,p} \right.} \right) = 0$, as $p \to \infty$ is similarly derived.

Claim 1 together with (5), in the main text, imply that for $p$ sufficiently large, $\Pi_{E} \left( {s,p} \right) > 0$, and the proof of Lemma 3 is completed.

Proof of Proposition 1. By part (i) of Lemma 2 and by (5), $\Pi_{E} \left( {s,p} \right)$ is continuous and non-decreasing in $p$. This follows from the fact that $Prob\left( {H\left| {s,p} \right.} \right)$ is continuous and non-decreasing in $p$, $\Delta_{E} \left( H \right) > 0$, $Prob\left( {L\left| {s,p} \right.} \right) = 1 - Prob\left( {H\left| {s,p} \right.} \right)$ and $\Delta_{E} \left( L \right) < 0$.

By Lemma 3, $\Pi_{E} \left( {s,p} \right) < 0$ for small $p$ and $\Pi_{E} \left( {s,p} \right) > 0$ for sufficiently large $p$.

Let

$$p_{h} = \max \left\{ {p \ge 0\left| {\Pi_{E} \left( {h,p} \right) \le 0} \right.} \right\}$$

$$p_{l} = \max \left\{ {p \ge 0\left| {\Pi_{E} \left( {l,p} \right) \le 0} \right.} \right\}$$

By the continuity of $\Pi_{E} \left( {s,p} \right)$ in $p$,

$$\Pi_{E} \left( {h,p_{h} } \right) = \Pi_{E} \left( {l,p_{l} } \right) = 0$$

(A6)

and E enters the market if and only if it observes either $\left( {h,p} \right)$ such that $p > p_{h}$ or $\left( {l,p} \right)$ such that $p > p_{l}$.

By part (ii) of Lemma 2, it is easy to verify that

$$\Pi_{E} \left( {h,p} \right) > \Pi_{E} \left( {l,p} \right)$$

(A7)

By (A6) and (A7)

$$\Pi_{E} \left( {l,p_{l} } \right) = \Pi_{E} \left( {h,p_{h} } \right) > \Pi_{E} \left( {l,p_{h} } \right)$$

and since $\Pi_{E} \left( {s,p} \right)$ is non-decreasing in $p$, we have $p_{l} > p_{h}$.

Proof of Lemma 4. First, suppose that $p_{H}^{M} \le p_{h}$. Then also $p_{L}^{M} < p_{h}$ and, according to Proposition 1, E stays out whether it observes $p_{L}^{M}$ or $p_{H}^{M}$. Hence, both types of M will set their (different) monopoly prices, giving a contradiction.

Next, suppose that $p_{L}^{M} < p_{h}$ and $p_{H}^{M} > p_{h}$. Since $\alpha \le \overline{\alpha }_{h}$, E stays out and $p^{*} \le p_{h}$. Therefore, $p^{*} = p_{L}^{M}$. In this case, H is better off by deviating to $p_{h}$ since

$$\Pi_{H} \left( {p_{L}^{M} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{h} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right)$$

implies that $p_{L}^{M} \ge p_{h}$, which is a contradiction.

The incentive compatibility condition when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ .

Proof of Lemma 5 ($ICC_{H}$). Considering the discussion about the relevant $ICC_{H}$ in the main text, for $p^{*}$ to be a pooling equilibrium price of H, the following should hold,

$$\Pi_{H} \left( {p^{*} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + \left\{ \begin{gathered} \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right),\,\,\,if\,p_{h} < p_{H}^{M} \le p_{l} \hfill \\ D_{H} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,p_{H}^{M} > p_{l} \hfill \\ \end{gathered} \right.$$

The first inequality implies that

$$\Pi_{H} \left( {p^{*} } \right) \ge \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right)$$

Recalling that $D_{H} = \Pi_{H} \left( {\hat{p}} \right)$ and the definition of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$ in the main text, $\Pi_{H} \left( {p^{*} } \right) \ge \Pi_{H} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)} \right)$ implies that $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$.

The second inequality requires that $\Pi_{H} \left( {p^{*} } \right) \ge D_{H}$ or that $p^{*} \ge \hat{p}$.

Additionally, another potential deviation is the following. When $p_{H}^{M} > p_{l}$ H may deviate to $p_{l}$, where E enters with probability $\alpha$. To avoid this deviation,

$$\Pi_{H} \left( {p^{*} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{l} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right)$$

Since $p_{H}^{M} > p_{l}$ and, by above, $p^{*} \ge \hat{p}$, take without loss of generality $p^{*} = \hat{p}$. Then

$$D_{H} + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{l} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right)$$

(A8)

Recalling the definition of $\tilde{p}_{H} \left( \alpha \right)$ in the main text, inequality (A8) is satisfied whenever $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$.

Proof of Lemma 6 ($ICC_{L}$). Considering the discussion about the relevant $ICC_{L}$ in the main text, to avoid deviations, and, therefore, for $p^{*}$ be a pooling equilibrium price of L, the following should hold,

$$\Pi_{L} \left( {p^{*} } \right) + \Pi_{L} \left( {p_{L}^{M} } \right) \ge \Pi_{L} \left( {p_{L}^{M} } \right) + \left\{ \begin{gathered} \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} ,\,\,\,\,\,if\,p_{h} < p_{L}^{M} \le p_{l} \hfill \\ D_{L} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,p_{L}^{M} > p_{l} \hfill \\ \end{gathered} \right.$$

Recall that $D_{L} = \Pi_{L} \left( {p_{0} } \right)$ and the definition of $\tilde{p}_{L} \left( \alpha \right)$ in the main text. Then the first inequality above is satisfied whenever $p_{L}^{M} > p^{*} \ge \tilde{p}_{L} \left( \alpha \right)$.

For the second inequality, it suffices that $p^{*} \ge p_{0}$. To deter deviation to $p_{l}$, when $p_{L}^{M} > p_{l}$, take $p^{*} = p_{0}$, then

$$D_{L} + \Pi_{L} \left( {p_{L}^{M} } \right) \ge \Pi_{L} \left( {p_{l} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L}$$

(A9)

Therefore, a pooling $p^{*} \ge p_{0}$ avoids a deviation to $p_{l}$ whenever, for example, first-period profits from $p^{*} = p_{0}$, plus the difference between second-period expected profits from the pooling and those from the deviation are greater than or equal to the profits from $p_{l}$. Taking into account the definition of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ in the main text, this implies that (A9) is satisfied whenever $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) \ge p_{l}$.

Proof of Lemma 7. Suppose first that $p_{H}^{M} \le p_{h}$. Then also $p_{L}^{M} < p_{h}$ and both L and H are better off deviating to their monopoly prices. Hence $p_{H}^{M} > p_{h}$.

Now suppose that $p_{L}^{M} = p_{h}$, then for any $p^{*} \in \left( {p_{h} ,p_{l} } \right]$,

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + \Pi_{L} \left( {p_{L}^{M} } \right)$$

which is a contradiction. Consider that $p_{l} > p_{L}^{M} > p_{h}$ and $p_{H}^{M} \le p_{l}$, then for any $p^{*}$,

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L}$$

The above is impossible unless $p^{*} = p_{L}^{M}$. Therefore, L will deviate to $p_{L}^{M}$. This is similarly true for H, which will deviate to $p_{H}^{M}$.

Finally, consider that $p_{h} < p_{L}^{M} < p_{l}$ and $p_{H}^{M} > p_{l}$, then L will deviate to $p_{L}^{M}$, and H will be better off deviating to $p_{l}$. Therefore, $p_{L}^{M} \ge p_{l}$, and Lemma 7 follows.

The incentive compatibility condition when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$ .

Proof of Lemma 8 ($ICC_{H}$). We have that $\overline{\alpha }_{h} < \alpha < 1$ and hence that E enters if it observes signal $h$. Also, $p_{H}^{M} > p_{l}$ (according to Lemma 7). Then, for H not to deviate to $p_{H}^{M}$ at a pooling $p^{*} \in \left( {p_{h} ,p_{l} } \right]$,

$$\Pi_{H} \left( {p^{*} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + D_{H}$$

or

$$\Pi_{H} \left( {p^{*} } \right) \ge \alpha \Pi_{H} \left( {p_{H}^{M} } \right) + \left( {1 - \alpha } \right)D_{H} = \Pi_{H} \left( {\tilde{p}_{H} \left( \alpha \right)} \right)$$

where $\tilde{p}_{H} \left( \alpha \right)$ is defined in the main text. Then, $p^{*} \ge \tilde{p}_{H} \left( \alpha \right)$.

Notice that H might have incentives to deviate to $p_{h}$. To deter this deviation, let us assume that $p^{*} = \tilde{p}_{H} \left( \alpha \right)$. Then

$$\Pi_{H} \left( {\tilde{p}_{H} \left( \alpha \right)} \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{h} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right)$$

By the definition of $\tilde{p}_{H} \left( \alpha \right)$ in the main text, the above inequality is equivalent to $D_{H} \ge \Pi_{H} \left( {p_{h} } \right)$ or $\hat{p} \ge p_{h}$. The result of Lemma 8 follows.

Proof of Lemma 9 ($ICC_{L}$). To deter deviations by L to $p_{L}^{M}$ when $p_{L}^{M} > p_{l}$, a pooling price has to satisfy,

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + D_{L}$$

or

$$\Pi_{L} \left( {p^{*} } \right) \ge \left( {1 - \alpha } \right)\Pi_{L} \left( {p_{L}^{M} } \right) + \alpha D_{L} = \Pi_{L} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right)$$

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ is defined in the main text. Then, $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$.

To avoid a deviation to $p_{h}$, consider that $p^{*} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$. Then,

$$\Pi_{L} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{h} } \right) + \Pi_{L} \left( {p_{L}^{M} } \right)$$

By the definition of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ in the main text, the above inequality implies $D_{L} \ge \Pi_{L} \left( {p_{h} } \right)$ or $p_{0} \ge p_{h}$ and Lemma 9 follows.

The incentive compatibility condition when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$.

By the discussion before Corollary 2 in the main text, $\overline{\alpha }_{h} < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \overline{\alpha }_{l} < 1$. Hence $\alpha > \overline{\alpha }_{h}$ and $\alpha \notin A_{h}$, $\forall \alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$. Namely, if the IS sends signal $h$, E enters the market when price $p^{*}$ is observed, irrespective of the precision $\alpha$ of the IS. This case is also split into two subcases: 1) ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$ and 2) $\overline{\alpha }_{l} \le \alpha < 1$.

(1) Consider that ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$. In this case $\alpha \notin A_{l} \cup A_{h}$. Namely, E enters the market when price $p^{*}$ is observed, irrespective of the signal sent by the IS. Therefore, both H and L should select the prices $p_{H}^{M}$ and $p_{L}^{M}$, respectively. Together with $p_{L}^{M} < p_{H}^{M}$, this leads to the following corollary:

Corollary A1. No pooling equilibrium exists when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$.

(2) Suppose now that $\overline{\alpha }_{l} \le \alpha < 1$. In this case $\alpha \in A_{l} \backslash \overline{A}_{h}$. Namely, similarly to the case (b) in the main text, E enters the market when price $p^{*}$ is observed if the IS sends the signal $h$ and does not enter if the IS sends signal $l$. Hence,

Corollary A2. The properties of the pooling equilibria and the incentive compatibility conditions of H and L when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and $\overline{\alpha }_{l} \le \alpha < 1$ are the same as in the case in which $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$, but the relevant threshold for $\alpha$ is $\overline{\alpha }_{l}$, not $\overline{\alpha }_{h}$.

Proof of Proposition 2. Let us consider the four cases analyzed in the main text.

(a) Recall that in this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

First, consider that $p_{L}^{M} < \hat{p}$. The next lemma proves part 1.(i) of Proposition 1 when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

Lemma A1. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$,${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and $p_{L}^{M} < \hat{p}$, then $SPE = \emptyset$.

Proof: As stated in the main text, in every possible pooling equilibrium satisfying belief consistency $p^{*} \le p_{h}$. Together with Lemma 4, this implies that $p_{L}^{M} \ge p_{h} \ge p^{*}$, which is incompatible with the $ICC_{H}$, since either $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 5 (1)) or $p^{*} \ge \hat{p}$ (see Lemma 5 (2)). Hence $p_{L}^{M} \ge p^{*} = p_{h} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p} > p_{L}^{M}$, giving a contradiction.

The next lemma proves the first part of case 1.(ii) of Proposition 1.

Lemma A2. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and $p_{L}^{M} = \hat{p}$. Then if $p^{*} \in SPEP$, $p^{*} = \left\{ {p_{L}^{M} } \right\}$.

Proof: First we prove that $p_{L}^{M} \in SPEP$. By Lemma 4 $p_{L}^{M} \ge p_{h}$. Suppose that $p_{h} = p_{L}^{M} < p_{l} < p_{H}^{M}$. On the one hand, as stated in the main text, the only possible pooling equilibrium price satisfying belief consistency in this case is $p^{*} = p_{L}^{M}$. On the other hand, by Lemma 5 (2) $p_{H}^{M} > p^{*} \ge \hat{p}$ and H has no incentive to deviate to $p_{H}^{M}$ in this case since $p_{L}^{M} = \hat{p}$.

To avoid deviations by H to $p_{l}$, it suffices that $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$ (see Lemma 5 (2)).

For configurations $p_{L}^{M} > p_{h}$, belief consistency requires $p^{*} = p_{h}$ which is incompatible with the $ICC_{H}$, where either $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$ if $p_{h} < p_{H}^{M} \le p_{l}$, or $p^{*} \ge \hat{p}$ if $p_{H}^{M} > p_{l}$ (see Lemma 5 (1) and Lemma 5 (2) respectively), since $p_{L}^{M} = \hat{p}$. Hence, $SPE = \emptyset$ in these cases.

We now deal with the case $p_{L}^{M} > \hat{p}$, and prove part 1.(iii.1) of Proposition 1. Lemma A3 below proves this result. We show that $SPEP = \left\{ {p^{*} \left| {\hat{p} \le p^{*} \le p_{L}^{M} } \right.} \right\}$ for all $\alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

Lemma A3. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and $p_{L}^{M} > \hat{p}$. Then $SPEP = \left[ {\hat{p},\,p_{L}^{M} } \right]$.

Proof: First, note that the set

$$\left\{ {p^{*} \left| {\hat{p} \le p^{*} \le p_{L}^{M} } \right.} \right\} \subseteq SPEP$$

To see that this is the case, consider any configuration such that $p_{L}^{M} = p_{h}$ and $p_{H}^{M} > p_{l}$. As stated in the main text, the only possible pooling equilibrium price satisfying belief consistency in this case is $p^{*} = p_{L}^{M}$. Note that by the $ICC_{H}$, $p_{H}^{M} > p^{*} \ge \hat{p}$ (see Lemma 5.(2)), H has no incentive to deviate to $p_{H}^{M}$ in this case since $p_{L}^{M} > \hat{p}$.

To avoid deviations by H to $p_{l}$, by Lemma 5 (2) any $p^{*} > \hat{p}$ deters these deviations whenever $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$. Since $p^{*} = p_{L}^{M} > \hat{p}$, then no deviation takes place.

Next consider configurations such that $\hat{p} \le p_{h}$ and $p_{l} < p_{L}^{M} < p_{H}^{M}$. Clearly in this case (by belief consistency) $p^{*} = p_{h}$. By the $ICC_{H}$, $p^{*} \ge \hat{p}$ so that H does not deviate to $p_{H}^{M}$ (see Lemma 5 (2)) and by the $ICC_{L}$, $p^{*} \ge p_{0}$ so that L does not deviate to $p_{L}^{M}$ (see Lemma 6 (2)). Both incentive compatibility conditions are compatible since $\hat{p} > p_{0}$ (see Lemma 1).

To avoid deviations by both H and L to $p_{l}$, it suffices that, by Lemma 5 (2) $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$, and by Lemma 6 (2) $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) \ge p_{l}$, respectively.

Hence, $\hat{p} \le p^{*} = p_{h} < p_{l} < p_{L}^{M}$ for $\min \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \ge p_{l}$ is an incentive compatible pooling equilibrium that satisfies belief consistency.

Therefore, $\left\{ {p^{*} \left| {\hat{p} \le p^{*} \le p_{L}^{M} } \right.} \right\} \subseteq SPEP$ as claimed.

Next, we prove that $SPEP \subseteq \left[ {\hat{p},\,p_{L}^{M} } \right]$. On the one hand, for any configuration $\hat{p} \le p_{h} < p_{L}^{M}$, if a pooling exists, by belief consistency $p^{*} = p_{h}$ and therefore $p^{*} \in \left[ {\hat{p},\,p_{L}^{M} } \right]$. On the other hand, note that whenever $\hat{p} > p_{h}$ no equilibrium exists since by belief consistency $p^{*} = p_{h}$. This is not compatible with the $ICC_{H}$, $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 5 (1)) or $p^{*} \ge \hat{p}$ (see Lemma 5 (2)).

Therefore, if $p^{*} \in SPEP$, then $p^{*} \in \left[ {\hat{p},\,p_{L}^{M} } \right]$ as claimed.

(b) Recall that in this second case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$.

The next lemma completes the proofs of parts 1. (i) and 1.(ii) of Proposition 1.

Lemma A4. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$, $\overline{\alpha }_{h} < \alpha < 1$ and $p_{L}^{M} \le \hat{p}$, then $SPE = \emptyset$.

Proof: As stated in the main text, in every possible pooling equilibrium satisfying belief consistency in this case, $p_{h} < p^{*} \le p_{l}$. Together with Lemma 7, this implies that $p_{L}^{M} \ge p^{*}$, which is incompatible with the $ICC_{H}$, $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 8).

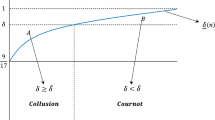
Now suppose that $\hat{p} < p_{L}^{M}$. Let us prove next that if $\overline{\alpha }_{h} < \alpha \le \delta$, then.

$SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$,

i.e., part 1.(iii.2) of Proposition 1.

Lemma A5. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$,$\overline{\alpha }_{h} < \alpha < 1$ and $\hat{p} < p_{L}^{M}$. Then

$$SPEP = \left\{ {p^{*} \left| {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p^{*} \le p_{L}^{M} } \right.} \right\}$$

and this set is non-empty if $\delta > \overline{\alpha }_{h}$ for all $\alpha$, $\overline{\alpha }_{h} < \alpha \le \delta$.

Proof: First, consider the case $p_{L}^{M} = p_{l}$. As stated in the main text, the only possible pooling equilibrium price satisfying belief consistency in this case is $p^{*} = p_{L}^{M}$. Note that the $ICC_{H}$ requires that $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 8), which in this case is equivalent to $p_{L}^{M} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$. Note that $p_{L}^{M} \ge \tilde{p}_{H} \left( \alpha \right)$ implies

$$\Pi_{H} \left( {p_{L}^{M} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + D_{H}$$

or that

$$\alpha \le \frac{{\Pi_{H} \left( {p_{L}^{M} } \right) - D_{H} }}{{\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} }} = \frac{{\Pi_{H} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {\hat{p}} \right)}}{{\Pi_{H} \left( {p_{H}^{M} } \right) - \Pi_{H} \left( {\hat{p}} \right)}} \equiv \delta$$

Clearly, $0 < \delta < 1$.

To avoid deviations by H and L to $p_{h}$, by Lemmas 8 and 9, it suffices that $p_{0} \ge p_{h}$ (see Lemma 1 (iii)). Hence $p^{*} = p_{L}^{M} > \hat{p}$, for $p_{0} \ge p_{h}$ and $\overline{\alpha }_{h} < \alpha \le \delta$, is an incentive compatible pooling equilibrium that satisfies belief consistency.

Notice now that if $p_{L}^{M} > p_{l}$, then, as stated in the main text, the unique pooling equilibrium guaranteeing belief consistency is $p^{*} = p_{l}$. The $ICC_{H}$ requires that $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 8), and the $ICC_{L}$ requires that $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ (see Lemma 9). Therefore $\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p_{l} = p^{*} < p_{L}^{M}$ should hold, where $\tilde{p}_{H} \left( \alpha \right) < p_{L}^{M}$ implies $\alpha < \delta$.

To deter deviations by both H and L to $p_{h}$, the $ICC_{H}$ given by Lemma 8 and the $ICC_{L}$ given by Lemma 9 again apply. Hence $\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p_{l} = p^{*} < p_{L}^{M}$, for $p_{0} \ge p_{h}$ and $\overline{\alpha }_{h} < \alpha < \delta$, is an incentive compatible pooling equilibrium that satisfies belief consistency.

Hence set $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$ as claimed.

Notice that the above implies part 1.(iii.3) of Proposition 1, i.e., for $\alpha > \delta$, $SPE = \emptyset$.

(c) In this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$. By Corollary A1, $SPE = \emptyset$ in this case (part 2.(ii.1) of Proposition 1).

(d) In this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and $\overline{\alpha }_{l} \le \alpha < 1$. By Corollary A2, this case is equivalent to the case (b) above, but the relevant threshold for $\alpha$ is $\overline{\alpha }_{l}$, not $\overline{\alpha }_{h}$. Hence, if $\hat{p} < p_{L}^{M}$, then.

$SPEP = \left\{ {p^{*} \left| {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p^{*} \le p_{L}^{M} } \right.} \right\}$,

and this set is non-empty if $\delta \ge \overline{\alpha }_{l}$ and for all $\alpha$, $\overline{\alpha }_{l} \le \alpha \le \delta$. This proves part 2.(ii.2) of Proposition 1. As above, note that 2.(ii.3) of the Proposition (i.e., for $\alpha > \delta$, $SPE = \emptyset$) is satisfied.

As in the proofs of parts 1.(i) and 1.(ii) of the Proposition (see Lemmas A1 and A2 above), if $p_{L}^{M} \le \hat{p}$, then $SPE = \emptyset$, which proves part 2.(i).

Finally, note that parts 2.(ii.1) and 2.(ii.3) of the Proposition imply the first part of point (3), while parts 1.(iii.1) and 1.(iii.3) imply the second part.

1.1 Example

1.1.1 Cournot competition

The equilibrium under Cournot competition in between L and E is characterized by $p_{0} = {{\left( {a + 2c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c_{L} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$ and $D_{L} = D_{E} \left( L \right) = {{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$; and the competition in between H and E is characterized by $\hat{p} = {{\left( {a + c_{L} + c_{H} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} + c_{H} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$, $D_{H} = {{\left( {a - 2c_{H} + c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{H} + c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$ and $D_{E} \left( H \right) = {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$. Note that $p_{L}^{M} = {{\left( {a + c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} > \hat{p} = {{\left( {a + c_{L} + c_{H} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} + c_{H} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$ since $c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

Consequently, under Cournot competition, Assumption 1, according to which $D_{E} \left( L \right) - K < 0$ and $D_{E} \left( H \right) - K > 0$, is satisfied for all $K$ such that ${{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} < K < {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$. Moreover, Assumption 3, according to which $\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$ is satisfied given that $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

1.1.2 Bertrand competition

The equilibrium under Bertrand competition in between L and E is characterized by $p_{0} = c_{L}$ and $D_{L} = D_{E} \left( L \right) = 0$; and the competition in between H and E is characterized by $\hat{p} = c_{H}$, $D_{H} = 0$ and $D_{E} \left( H \right) = \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$. Note that $p_{L}^{M} = {{\left( {a + c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} > \hat{p} = c_{H}$ since $c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

Consequently, under Bertrand competition, Assumption 1, according to which $D_{E} \left( L \right) - K < 0$ and $D_{E} \left( H \right) - K > 0$, is satisfied for all $K$ such that $0 < K < \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$. Moreover, Assumption 3, according to which $\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$ is satisfied given that $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

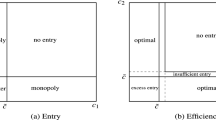
A sketch of the proof of Proposition 4. As stated in the main text, in this equilibrium, E identifies the type of M with probability 1. Hence, E enters the market when price $p_{H}$ is observed, irrespective of the signal of the IS, and E stays out when $p_{L}$ is observed, again irrespective of $s$. Therefore, by the entrant’s strategy, $p_{H} > p_{l}$ and $p_{L} \le p_{h}$. See Fig. 1 in the main text.

Knowing that entry will occur, the H-type monopoly is better off choosing the price $p_{H}^{M}$. Thus $SSE_{H} = \left\{ {p_{H}^{M} } \right\}$ and E enters for sure when it observes price $p_{H}^{M}$. In particular, $p_{H}^{M} > p_{l}$.

We need to prove that $SSE_{L} = \left\{ {p_{L} \left| {p_{0} \le p_{L} \le \min \left( {p_{L}^{M} ,\hat{p}} \right)} \right.} \right\}$ for all $\alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$. Hence, there are two relevant cases: when $p_{L}^{M} \le \hat{p}$ and when $\hat{p} < p_{L}^{M}$.

The proof follows two steps. The first step consists of showing that $p_{L} \in \left[ {p_{0} ,\min \left( {p_{L}^{M} ,\hat{p}} \right)} \right]$ in both cases $p_{L}^{M} \le \hat{p}$ and $\hat{p} < p_{L}^{M}$.

In the first case, when $p_{L}^{M} \le \hat{p}$, $p_{L} = p_{L}^{M}$ can be supported as a separating equilibrium price (no type of M has incentives to deviate), for instance when

$$p_{L} = p_{L}^{M} \le p_{h} \le \hat{p} < p_{l} \le \tilde{p}_{H} \left( \alpha \right) < p_{H}^{M}$$

And $p_{L} \in \left[ {p_{0} ,p_{L}^{M} } \right)$ can also be supported as a separating equilibrium price, for instance when

$p_{L} = p_{h} < p_{l} < p_{L}^{M} \le \hat{p} < \tilde{p}_{H} \left( \alpha \right) < p_{H}^{M}$.

Similarly, in the second case $\hat{p} < p_{L}^{M}$ $p_{L} \in \left[ {p_{0} ,\hat{p}} \right]$ can be supported as a separating equilibrium price, for instance when

$$p_{L} = p_{h} \le \hat{p} < p_{l} < \min \left( {p_{L}^{M} ,\tilde{p}_{H} \left( \alpha \right)} \right) < p_{H}^{M}$$

The second step of the proof is to show that if $p_{L} \notin \left[ {p_{0} ,\min \left( {p_{L}^{M} ,\hat{p}} \right)} \right]$, then $p_{L} \notin SSE_{L}$, which is easy to show considering the relevant positions of $p_{h}$ and $p_{l}$.