Abstract
Monotonicity is an appealing principle of relational power measures in social networks. It states that as the influence of an individual changes, the relational power measure should change in the same direction. We axiomatically characterize the \(\beta \)- and score-measures on directed networks using three axioms: two different monotonicity axioms, the same symmetry axiom and two different efficiency axioms, respectively. For every individual, the \(\beta \)-measure refers to a weighted sum over all dominated individuals by itself, in which for each dominated individual the weight is given by the reciprocal of the number of its dominators, while the score-measure refers simply to the number of dominated individuals by itself. We also extend the result for the score-measure to undirected networks.


Similar content being viewed by others
Notes
As an illustration, suppose that a node i has two predecessors. Node i contributes a value of one half to the relational power measure of each predecessor in the \(\beta \)-measure and contributes a value of one to the relational power measure of each predecessor in the score-measure.
A ranking method assigns to every network an ordering of the nodes. A relational power measure assigns every network with n nodes an n-dimensional vector of real numbers such that the ith component is a measure of the relational power of node i.
In cooperative games, the papers on the monotonicity axiom and related conditions are numerous; see, for example, Kalai and Smorodinsky (1975), Kalai and Samet (1985), Thompson and Myerson (1980), Thompson (1983), Young (1985), Hwang (2010). In particular, to emphasize its indispensability, Kalai and Samet (1985) stated that the monotonicity of a solution is a necessary and sufficient condition in order to bring about full cooperation.
The positive responsiveness refers to the maintenance of the monotonicity of the ranking in different networks. In particular, consider two distinct nodes i and j in two different networks. If the ranking of node i is not worse than the ranking of node j, then when the influence of node i increases, the ranking of node i should be strictly better than that of node j.
For any set X, the cardinality \(\#X\) is the number of elements belonging to X.
Note that the power scope is about its neighborhood (or the rooted tree of radius 1); and the amount of dominance over every dominating node j depends on the neighborhood of its neighbors, which implies that the rooted tree of radius 2 is considered.
We use (i, j) to denote the asymmetric relations in digraphs in Sect. 2 and \(\{i,j\}\) to denote the symmetric relations in undigraphs.
References
Abreu D, Manea M (2012) Bargaining and efficiency in networks. J Econ Theory 147:43–70
Behzad M, Chartrand G, Lesniak-Foster L (1979) Graphs and digraphs. Wadsworth, Belmont
Bloch F, Dutta B, Manea M (2019) Efficient partnership formation in networks. Theor Econ 14:779–811
Bonacich P (1987) Power and centrality: a family of measures. Am J Sociol 92:1170–1182
Bouyssou D (1992) Ranking methods based on valued preference relations: a characterization of the net flow method. Eur J Oper Res 60:61–67
Bouyssou D, Marchant T (2018) The \( \beta \)-ranking and the \( \beta \)-measure for directed networks: axiomatic characterizations. Soc Netw 52:145–153
Cook KS, Emerson RM, Gillmore MR, Yamagishi T (1983) Equity and commitment in exchange networks. Am Sociol Rev 89:275–305
Emerson RM (1962) Power-dependence relations. Am Sociol Rev 27:31–41
Freeman LC (1979) Centrality in social networks: conceptual clarification. Soc Netw 1:215–239
Gould RV (1987) Measures of betweenness in non-symmetric networks. Soc Netw 9:277–282
Goyal S (2016) Networks in economics: a perspective on the literature. In: Bramoulle Y, Galeotti A, Rogers B (eds) The Oxford handbook of the economics of networks. OUP, Oxford
Henriet D (1985) The Copeland choice function: an axiomatic characterization. Soc Choice Welf 2:49–63
Herings PJJ, van der Laan G, Talman D (2005) The positional power of nodes in digraphs. Soc Choice Welf 24:439–454
Hwang YA (2010) Marginal monotonicity solution of NTU games. Games Econ Behav 70:502–508
Jackson MO (2016) The past and future of network analysis in economics. In: Bramoulle Y, Galeotti A, Rogers B (eds) The Oxford handbook of the economics of networks. OUP, Oxford
Kalai K, Samet D (1985) Monotonic solutions to general cooperative games. Econometrica 53:307–327
Kalai K, Smorodinsky M (1975) Other solutions to Nash’s bargaining problem. Econometrica 43:513–518
Kendall MG (1955) Further contributions to the theory of paired comparisons. Biometrics 11:43–62
Manea M (2011) Bargaining in stationary networks. Am Econ Rev 101:2042–2080
Manea M (2016) Models of bilateral trade in networks. In: Bramoulle Y, Galeotti A, Rogers B (eds) The Oxford handbook of the economics of networks. OUP, Oxford
Markovsky B, Patton T, Willer D (1988) Power relations in exchange networks. Am Sociol Rev 53:220–236
Mullen B, Johnson C, Salas E (1991) Effects of communication network structure: components of positional centrality. Soc Netw 13:169–186
Rubinstein A (1980) Ranking the participants in a tournament. SIAM J Appl Math 38:108–111
Sadler E (2020) Ordinal centrality. https://doi.org/10.2139/ssrn.3594819
Thompson W (1983) Problems of fair division and the egalitarian solution. J Econ Theory 31:211–226
Thompson W, Myerson RB (1980) Monotonicity and independence axioms. Int J Game Theory 9:37–49
van den Brink R, Gilles RP (1994) An axiomatic social power index for hierarchically structured populations of economic agent. In: Gilles RP, Ruys PHM (eds) Imperfections and behaviour in economic organizations. North-Holland, Amsterdam
van den Brink R, Gilles RP (2000) Measuring domination in directed networks. Soc Netw 22:141–157
van den Brink R, Gilles RP (2003) Ranking by outdegree for directed graphs. Discrete Math 271:261–270
van den Brink R, Borm P, Hendrickx R, Owen G (2008) Characterizations of the \( \beta \)- and the degree network power measure. Theory Decis 64:519–536
Wei T (1952) The algebraic foundation of ranking theory. Ph.D. Thesis. Cambridge University, Cambridge
Young HP (1985) Monotonic solutions of cooperative games. Int J Game Theory 14:65–72
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We are indebted to an associate editor and two anonymous referees for helpful suggestions and comments. This work was financially supported by the National Science Foundation of China (No. 72071009, 71671010, 71690245).
Appendix
Appendix
Proof of Lemma 1
First, consider part (i). Since by condition (b), we have \(f_{i}(D)=f_{j}(D)\) for all \(i,j\in N_1\) by D-SYM of f. Combining this with condition (a), we have \(f_{i}(D)=\beta _{i}(D)\) for all \(i\in N\) by D-EFF of both f and \(\beta \). Then, consider part (ii). Since by condition (a), we have \(f_i(D)=f_i(D')\) and \(\beta _i(D)=\beta _i(D')\) by D-MON of both f and \(\beta \). Combining this with condition (b), we have \(f_i(D)=\beta _i(D)\). \(\square \)
Proof of Theorem 1
It can easily be verified that the \(\beta \)-measure satisfies the three axioms. To prove the converse, suppose that f is a relational power measure satisfying D-MON, D-EFF and D-SYM.
Step 1: First, we prove that for every \(D\in {\mathscr {D}}\), if i is a dummy node, then \(f_{i}(D)=0\). Two cases are distinguished.
Case 1: \(D=\emptyset \).
Since \(P_{D}(i)=\emptyset \) for all \(i\in N\), by D-EFF and D-SYM of f, we have
Case 2: \(D\ne \emptyset \).
Let \(D_{\emptyset }\in {\mathscr {D}}\) denote the empty digraph; that is, \(D_{\emptyset }=\emptyset \). Let \(i\in N\) be a dummy node in D. Since \(S_{D}(i)=S_{D_{\emptyset }}(i)=\emptyset \), by Case 1 and D-MON of f,
Hence, a dummy node always obtains the measure 0.
Step 2: Now consider the case that i is not a dummy node in D.
where the subgraph \(D_{j}\) is defined by node j and j’s predecessors.
Let I denote the number of nonempty subgraphs in Eq. (3); that is, \(I=\#\{j\in N: D_{j}\ne \emptyset \}\). The proof proceeds by induction. If \(I=0\), \(D=\emptyset \), and then by Step 1, \( f_{i}(D)=\beta _{i}(D)=0 \) for all \(i\in N\). If \(I=1\), suppose that \(D=D_{j_{0}}\) for some \(j_{0}\in N\). It is straightforward to see that for all \(i\in N\setminus P_{D}(j_{0})\), i is a dummy node; hence, by Step 1, \(f_{i}(D)=\beta _{i}(D)=0\). Next, for all \(j,j'\in P_{D}(j_{0})\), \(S_{D}(j)=S_{D}(j')=\{j_{0}\}\) and \(P_{D}(j)=P_{D}(j')=\emptyset \). By D-SYM of both f and \(\beta \), it has to be true that \(f_{j}(D)=f_{j'}(D) \) and \(\beta _{j}(D)=\beta _{j'}(D)\). Together with the D-EFF of both f and \(\beta \), \(f_{j}(D)=\frac{1}{\# P_{D}(j_{0})}=\beta _{j}(D)\) for all \(j\in P_{D}(j_{0})\). Therefore, \(f(D)={\beta }(D)\) whenever I is 0 or 1.
Now, assume that \(f(D)=\beta (D)\) whenever the number of nonempty subgraphs in Eq. (3) is at most \(I^{*}\) (i.e., \(I\le I^{*}\)) for any strictly positive integer \(I^{*}\le n-1\). We then consider the case \(I=I^{*}+1\). Suppose that \(D_{j_{1}},\ldots ,D_{j_{I^{*}+1}}\) are these nonempty subgraphs and \(D=\bigcup _{k=1}^{I^{*}+1} D_{j_{k}}\). Let \(R=\bigcap _{k=1}^{I^{*}+1}P_{D_{j_{k}}}(j_{k})\). Consider a node \(i\in N\). Two cases are distinguished.
Case A: \( i\notin R\).
If \(i\notin P_{D_{j_{k}}}(j_{k})\) for any \(1\le k\le I^{*}\), i is a dummy node. By Step 1, we are done. If there exists an integer \(0<q\le I^{*}\), such that \( i\in \bigcap _{k=1}^{q} P_{D_{j_{k}}}(j_{k})\). We define a new digraph \(D'=\bigcup _{k=1}^{q}{D_{j_{k}}}\). Since \(S_{D}(i)=\{j_{1},j_{2},\ldots ,j_{q}\}=S_{D'}(i)=\{j_{1},\ldots ,j_{q}\}\) and \(P_{D}(j)=P_{D'}(j)\) for any \(j\in \{j_{1},\ldots ,j_{q}\}\), by D-MON of both f and \(\beta \), we have
By induction, it is known that \(f_{i}(D')={\beta }_{i}(D')\). The above equalities yield that \(f_{i}(D)={\beta }_{i}(D)\).
Case B: \( i\in {R}\).
For every \(i'\in R\), it is straightforward to see that that \(S_{D}(i')=\{j_{1},j_{2},\ldots ,j_{I^{*}+1}\}\) and \(P_{D}(i')=\emptyset \). By D-SYM of f, there exists a constant \(c\in {\mathbb {R}}\) such that \(f_{i'}(D)=c\) for all \(i'\in R\). In the same manner, by D-SYM of \(\beta \), there exists a constant \(c'\in {\mathbb {R}}\) such that \(\beta _{i'}(D)=c'\) for all \(i'\in R\). Note that Case A shows that for any \(j\notin R\), \(f_{j}(D)=\beta _{j}(D)\). By D-EFF of both f and \(\beta \), it has to be true that \(c=c'\). \(\square \)
The following example proves the independence of the three axioms in Theorem 1.
Example 6
In this example, we provide three alternative relational power measures for digraphs such that each one satisfies two but not all three of the axioms presented in Theorem 1.
-
1.
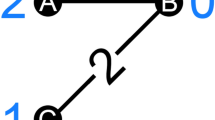
It is straightforward to see that the score-measure \(\sigma \) satisfies D-MON and D-SYM, but it does not satisfy D-EFF. For the digraph \(D'\) illustrated by the right panel of Fig. 1, the \(\beta \)-measure is \(\beta (D')=(\frac{1}{2},0,\frac{1}{2})\) and the score-measure is \(\sigma (D')=(1,0,1)\).
-
2.
Let the relational power measure \( f^{1}:{\mathscr {D}}\rightarrow {\mathbb {R}}^{N}\) be given by for every \(D \in {\mathscr {D}}\) and \(i\in N \),
$$\begin{aligned} f_{i}^{1}(D)=\left\{ \begin{array}{lcl} \sum _{j\in {S_{D}(i)}}{1}&{} &{} \text { if }i=1; \\ \sum _{j\in S_{D}(i) {\setminus } S_{D}(1)} \frac{1}{\#[P_{D}(j)]}&{} &{} \text {otherwise}. \end{array} \right. \end{aligned}$$This function \(f^1\) satisfies D-EFF and D-MON, but it does not satisfy D-SYM. For the digraph \(D'\) illustrated by the right panel of Fig. 1, \(f^1(D')=(1,0,0)\ne \beta (D')\).
-
3.
Let the relational power measure \( f^{2}:{\mathscr {D}}\rightarrow {\mathbb {R}}^{N}\) be given by for every \(D \in {\mathscr {D}}\) and \(i\in N \),
$$\begin{aligned} f_{i}^{2}(D)=\frac{\#\{j\in {N}|P_{D}(j)\ne \emptyset \} }{\#N}. \end{aligned}$$This function \(f^2\) satisfies D-EFF and D-SYM, but it does not satisfy D-MON. For the digraph \(D'\) illustrated by the right panel of Fig. 1, \(f^2(D')=(\frac{1}{3},\frac{1}{3},\frac{1}{3})\ne \beta (D')\).
The following example proves the independence of the three axioms in Theorem 2 (or Theorem 3).
Example 7
In this example, we provide three alternative relational power measures for digraphs such that each one satisfies two but not all three axioms presented in Theorem 3 (or Theorem 2).
-
1.
Let the relational power measure \(f^{3}:{\mathscr {D}}\rightarrow {\mathbb {R}}^{N}\) be given by for every \(D \in {\mathscr {D}}\) and \(i\in N\),
$$\begin{aligned} f_{i}^{3}(D)=\big \{ \#[S_{D}(i)]\big \}^{2}. \end{aligned}$$The function \(f^3\) satisfies D-SYM, D-MON and D-SMON, but it does not satisfy D-SEFF. For the digraph \(D'\) illustrated by the right panel of Fig. 2, \(f^3(D')=(4,0,0)\ne \sigma (D')=(2,0,0)\).
-
2.
Let the relational power measure \(f^{4}:{\mathscr {D}}\rightarrow {\mathbb {R}}^{N}\) be given by for every \(D \in {\mathscr {D}}\) and \(i\in N \),
$$\begin{aligned} f_{i}^{4}(D)=\left\{ \begin{array}{lcl} \#[S_{D}(i)]-\Upsilon (S_{D}(i)) &{} &{} \text {if } i=1; \\ \#[S_{D}(i)]+\frac{1}{N-1}\Upsilon (S_{D}(1))&{} &{} \text {otherwise} \end{array} \right. \end{aligned}$$where \(\Upsilon : 2^{N}\rightarrow \{0,1\}\) is defined as for any \(N'\subset N\), \(\Upsilon (N')=0\) if and only if \(N'=\emptyset \). The function \(f^4\) satisfies D-SEFF, D-MON and D-SMON, but it does not satisfy D-SYM. For the digraph \(D'\) illustrated by the right panel of Fig. 1, \(f^4(D')=(0,\frac{1}{2},\frac{3}{2})\ne \sigma (D')=(1,0,1)\).
-
3.
Let the relational power measure \( f^{5}:{\mathscr {D}}\rightarrow {\mathbb {R}}^{N}\) be given by for every \(D \in {\mathscr {D}}\) and \(i\in N\),
$$\begin{aligned} f_{i}^{5}(D)=\frac{\#D}{\#N}. \end{aligned}$$The function \(f^5\) satisfies D-SEFF and D-SYM, but it does not satisfy D-MON (hence it does not satisfy D-SMON). For the digraph \(D'\) illustrated by the right panel of Fig. 2, \(f^5(D')=(\frac{2}{3},\frac{2}{3},\frac{2}{3})\ne \sigma (D')=(2,0,0)\).
Proof of Proposition 1
We only focus on the “converse part” of the statement 2. Other parts can be easily verified, and we omit the corresponding proof.
The proof is proceeded by developing a relational power measure f that satisfies D-IND and D-DWMON but it violates D-MON as follows. Let \(f:{\mathscr {D}} \rightarrow {\mathbb {R}}^{N}\) be given by for every \(D\in {\mathscr {D}}\) and \(i\in N\),
It is straightforward to see that f satisfies D-IND and D-DWMON. Note that given that \(S_D(i)=\{j\}\), \(f_{i}(D)\) increases from 1/2 to 1 when \(\#P_D(j)\) increases from 2 to 3, which implies that f violates D-MON. \(\square \)
Proof of Proposition 2
The proof proceeds by developing a relational power measure \(f^{*}\) that satisfies the three axioms but differs from the \(\beta \)-measure. Let \(D^{*}\in {\mathscr {D}}\) be defined as \(D^{*}=\{(1,2)\}\), i.e.,
Let the relational power measure \(f^{*}:{\mathscr {D}} \rightarrow {\mathbb {R}}^{N}\) be given by for every \(D\in {\mathscr {D}}\) and \(j\in N\),
Note that \(\beta _{1}(D^{*})=1\) and \(\beta _j(D^{*})=0\) for any \(j\in N\setminus \{1\}\). Clearly, for the digraph \(D^{*}\), \(f^{*}\ne \beta \). It is easy to see that the relational power measure \(f^{*}\) satisfies D-DEFF and D-SYM. It remains to verify that f satisfies D-STMON (hence it also satisfies D-WMON). First, if \(D^{*}\) is neither D nor \(D'\) in the statement of D-STMON, by the definition of \(f^{*}\), \(f^{*}(D)=\beta (D)\) and \(f^{*}(D')=\beta (D')\). By D-STMON of \(\beta \), we have done. We now proceed to consider the case that \(D^{*}=D\) and the case that \(D^{*}=D'\).
Case A: \(D^{*}=D\) in the statement of D-STMON.
Subcase A1: \(i=1\) in the statement of D-STMON.
Clearly, \(S_{D^{*}}(1)=\{2\}\) and \(P_{D^{*}}(2)=\{1\}\). Therefore, for any \(D'\) obtained from \(D^{*}\) in D-STMON, it must be true that “adding nodes to \(S_{D^{*}}(1)\)”. This implies that \(S_{D'}(1)\supsetneq S_{D^{*}}(1)\). By the definitions of both \(f^{*}\) and \(\beta \), we have that \(f^{*}_{1}(D')=\beta _{1}(D')\ge 1+\frac{1}{n-1}\). Therefore,
Subcase A2: \(i= 2\) in the statement of D-STMON.
Note that the node 2 is a dummy node. It implies that for any \(D'\) obtained from \(D^{*}\) in D-STMON, it must be true that “adding nodes to \(S_{D^{*}}(2)\)”. Then, if follows that
Case B: \(D^{*}=D'\) in the statement of D-STMON.
Subcase B1: \(i=1\) in the statement of D-STMON.
It must be true that D is either the empty graph or \(P_{D}(2)\) contains at least one another node, except node 1. By the definition of \(f^{*}\), we have that
Subcase B2: \(i\ne 2\) in the statement of D-STMON.
Since the node 2 is a dummy node in \(D^{*}\)(or \(D'\)), this case can not happen. \(\square \)
Proof of Proposition 3
The proof proceeds by developing a relational power measure \(f^{**}\) that satisfies the three axioms but differs from the score-measure. By replacing \(\beta \) with \(\sigma \) in the definition of \(f^{*}\) in the proof of Proposition 2, we obtain the relational power measure \(f^{**}\). Formally, for every \(D\in {\mathscr {D}}\) and \(j\in N\),
The proof proceeds in the same manner as the proof of Proposition 2, we omit it. \(\square \)
Proof of Theorem 6
It can easily be verified that the score-measure satisfies U-SEFF, U-SYM and U-SMON. To prove the converse, suppose that p is a relational power measure satisfying the three axioms. To facilitate the proof, the following notation is introduced. For every \(G\in {\mathcal {G}}\) and \(i\in N\), let \(G_{i}=\big \{\{i,j\}|j\in R_{G}(i)\big \}\) denote the undigraph where only the edges between i and its neighbors are preserved.
Step 1: We prove that for every \(G\in {\mathcal {G}}\) and \(i\in N\), if i is an isolated node in G, then \(p_{i}(G)=\sigma ^{u}_{i}(G)=0\). Two cases can be distinguished.
Case 1.1: \(G=\emptyset \).
Since \(R_{G}(j)=\emptyset \) for all \(j\in {N}\), by both U-SEFF and U-SYM of p,
Case 1.2: \( G\ne \emptyset .\)
Let \(G_{\emptyset }\) denote the empty undigraph over all nodes in N; that is, \(G_{\emptyset }=\emptyset \). Let \(i\in N \) be an isolated node in G. Since \(R_{G}(i)=\emptyset \) and \(R_{G_{\emptyset }}(i)=\emptyset \), by Case 1.1 and U-SMON of p,
Hence, an isolated node always obtains the measure 0.
Step 2: We show that for every \(G\in {\mathcal {G}}\) and \(i\in N\), if node i is pending in G, then \(p_{i}(G)=\sigma ^{u}_{i}(G)=1\). As in step 1, two cases can be distinguished.
Case 2.1: \(G=\big \{\{i,j\}\big \}\).
Any node \(k\in N\setminus \{i,j\}\) is isolated in G. Step 1 says that \(p_{k}(G)=0\). Note that \(R_{G}(j){\setminus }\{i\}=R_{G}(j){\setminus }\{i\}\). By U-SYM of p, \(p_{i}(G)=p_{j}(G)\). By U-SEFF,
Case 2.2: G is not a singleton.
Suppose that \(\{ij\}\in G\). Note that \(R_{G}(i)=R_{G_{i}}(i)=\{j\}\). By Case 2.1 and U-SMON of p,
Step 3: We prove that for every \(G\in {\mathcal {G}}\) and \(i\in N\), if node i is neither isolated nor pending in G, then \(p_{i}(G)=\sigma ^{u}_{i}(G)\). Two cases can be distinguished.
Case 3.1: \(G=G_{i}\).
Any node \(k\notin \{i\}\cup R_{G}(i)\) is isolated in G, and by Step 1, \(p_{k}(G)=0\). Further, any node \(j\in R_{G}(i)\) is pending in G, and by Step 2, \(p_{j}(G)=\sigma ^{u}_{j}(G)=1\). By U-SEFF,
Case 3.2: \(G\ne G_{i}\).
Note that \(R_{G}(i)=R_{G_{i}}(i)\). By Case 3.1 and U-SMON of p, \(p_{i}(G)=\sigma ^{u}_{i}(G)=\#[R_{G}(i)]\). \(\square \)
The following example proves the independence of the three axioms stated in Theorem 6.
Example 8
In this example, we provide three alternative relation power measures for undigraphs such that each one satisfies two but not all three axioms in Theorem 6.
-
1.
Let the relational power measure \(p^{1}:{\mathcal {G}} \rightarrow {\mathbb {R}}^{N}\) be given by for every \(G\in {\mathcal {G}}\) and \(i\in N\),
$$\begin{aligned} p_{i}^{1}(G)=\big \{ \#[R_{G}(i)]\big \}^{2}. \end{aligned}$$The function \(p^{1}\) satisfies U-SYM and U-SMON, but it does not satisfy U-SEFF.
-
2.
Let the relational power measure \(p^{2}:{\mathcal {G}} \rightarrow {\mathbb {R}}^{N}\) be given by for every \(G\in {\mathcal {G}}\) and \(i\in N\),
$$\begin{aligned} p_{i}^{2}(G)=\left\{ \begin{array}{lcl} \#[R_{G}(i)]-1&{} &{} \text {if } i=1; \\ \#[R_{G}(i)]+\frac{1}{N-1}&{} &{} \text {otherwise}. \end{array} \right. \end{aligned}$$The function \(p^{2}\) satisfies U-SEFF and U-SMON, but it does not satisfy U-SYM.
-
3.
Let the relational power measure \(p^{3}:{\mathcal {G}} \rightarrow {\mathbb {R}}^{N}\) be given by for every \(G\in {\mathcal {G}}\) and \(i\in N\),
$$\begin{aligned} p_{i}^{3}(G)=\frac{2\#G}{\#N} \end{aligned}$$The function \(p^{3}\) satisfies U-SEFF and U-SYM, but it does not satisfy U-SMON.
Rights and permissions
About this article
Cite this article
Cui, Z., Hwang, YA. & You, DC. Axiomatizations of the \(\beta \) and the score measures in networks. Int J Game Theory 50, 399–418 (2021). https://doi.org/10.1007/s00182-020-00752-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-020-00752-y