Abstract
This paper studies a war of attrition in which players have private and asymmetric resource constraints. We show that resource inequality, measured by whether and by how much a player can fight longer than her opponent, is a key measure of strength in a war of attrition. In the unique equilibrium surviving a refinement, players with more resources always fight and players with fewer resources fight to develop a reputation of “deep pocket” until they deplete their resources. As a result, private resource constraints and resource inequality often exacerbate the outcome inequality. Furthermore, changes in resource inequality have a non-monotonic effect on the length of the war, which is consistent with empirical findings. Finally, we extend the results to the case with a continuum of resource levels to further examine the impact of resource inequality.
Similar content being viewed by others
Notes
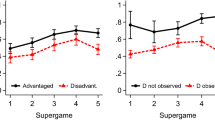
Many wars of attrition in business end up being exceedingly costly. In the striking case between the British Satellite Broadcasting and Sky TV, the total costs of the two-year war of attrition were about £1.25 million, which resulted in a merger between the two companies (McAfee 2005). In another famous example, Best Buy and Circuit City were caught in price wars, which we might model as a war of attrition, in the consumer electronics market, and over more than ten years’ price competition Circuit City went bankrupt and exited the market (McGuigan et al. 2016).
There is considerable evidence of unions collecting and suggesting they have large war chests before impending wage bargaining. See United Auto Workers war chest, Verizon war chest, German Auto Workers war chest among others. One caveat is that in some examples the prizes can be divisible and allocations are determined through bargaining, whereas we consider a setting with an indivisible prize.
Baye et al. (2005) argue that an “undesirable feature of the British system is that it might make courts a playing field for only the wealthy. Under the British system, the prospect of having to pay the winner’s legal expenses might preclude the poor from seeking justice through the court system.”
Having a limited war chest also implies that the amount of unions can strike is limited. The size of war chest or how much unions pay out in the event of a strike may be private information, thus unions may have a private deadline to end the strike by. In inter-firm groups, team members face deadlines for their deliverable and may engage in a war of attrition to see who concedes and carries out the task first. The team members can privately know their own productivity which affects how long they can procrastinate before needing to do the task.
For example, there is empirical evidence that highlights the positive correlation between firms’ financial constraints and their innovative performances. See Schroth and Szalay (2010), Hall et al. (2016), and the references therein. Wealth difference among applicants is rooted in the US college admission process (Avery et al. 2003), as both preparation and application are costly for the students. In a study of litigation Yoon (2010) provides evidence that a party’s wealth significantly affects the legal outcomes.
The literature on wars of attrition is large and has many applications, including biological competitions (Smith 1974; Riley 1980), industry shakeouts (Fudenberg and Tirole 1986), public good problems (Bliss and Nalebuff 1984), patent races (Leininger 1991), business standard settings (Farrell and Simcoe 2012), litigation (Kennan and Wilson 1989), bilateral bargaining (Chatterjee and Samuelson 1987; Abreu and Gul 2000), politics (Alesina and Drazen 1991; Fearon 1998; Dekel et al. 2008, 2009), and wars (Powell 2017).
Unlike in the discrete model, we are only able to characterize the monotone equilibrium instead of all equilibria in the continuum setting.
See Krishna and Morgan (1997) for an early analysis of the static all-pay auctions and wars of attrition with symmetric bidders and no budget limits. Che and Gale (1996) show that all-pay auctions revenue dominate first-price sealed-bid auctions with symmetric budget constraints. Bobkova (2020) studies two-bidder first-price auctions with asymmetric budget constraints. Also see Siegel (2009), Olszewski and Siegel (2016) and Olszewski and Siegel (2019) for general analysis of all-pay contests.
Multiple equilibria lead to difficulties in revenue comparisons and comparative statics. A common method to obtain uniqueness in the literature is to specify perturbations of the original game. See for example Kornhauser et al. (1989), Myatt (2005) and Georgiadis et al. (2019). Nevertheless, different perturbations can lead to selections of different equilibria. As a comparison, we do not refer to perturbations and show that equilibria in our setting are of at most two kinds.
For completeness we also analyze the one-sided private information case in the supplemental appendix.
Both assumptions are innocuous since we will focus on the limiting case in which \(\varepsilon \) is close to zero as an approximation of the standard continuous-time wars of attrition.
See Mas-Colell et al. (1995) Definition 9.C.3 for a formal definition of wPBE. In our model with binary types, it can be shown that weak perfect Bayesian equilibrium is equivalent to sequential equilibrium.
The uniqueness follows from the finite-budget assumption: if both players’ budgets are infinite, then there are multiple equilibria as in the complete-information war of attrition without budget constraints. The asymmetry here follows from the asymmetric tie-breaking assumption.
The proofs of this lemma and other results in the main text are in the appendix 1.
Stating the definition of \(\alpha \) this way allows ease of exposition later in the example.
The same argument applies to periods later than \(2T+3\).
For example, in any period \(t>2T\) only 1h and 2h can bid, so we must have \(\rho _{t+1}=1\) and \(\eta _{t+2}=1\).
This does not necessarily occur in the first two periods due to the asymmetric tie-breaking assumption.
In Example 4.3 we show the results hold when the hazard rates are constant for a parametric case.
We will show that the equilibrium is strictly increasing in budget levels, which implies that tie-breaking rules do not matter here.
This is in contrast to the monotone pure-strategy equilibria in private value models where players have strict incentives to concede at certain times depending on their values.
See Bulow and Klemperer (1999) for an elegant study of a \((N+K)\)-player and N-prize generalized war of attrition without budget constraints where each player has a unit demand.
If \(V_2>B_h\), then Proposition 3.5 implies that 2h always bids in any wPBE, so there is no off-equilibrium history where player 2 concedes for sure.
Otherwise, 2l can deviate to bidding, in which case player 1 will concede in the next period.
Note that \(\rho _{2T-1}=\rho _{2T-2}\).
This argument is related to the proof in Abreu and Gul (2000) that shows uniqueness of the concession probability distribution in a reputational bargaining with two-sided behavioral types.
References
Abreu D, Gul F (2000) Bargaining and reputation. Econometrica 68(1):85–117
Abreu D, Pearce D, Stacchetti E (2015) One-sided uncertainty and delay in reputational bargaining. Theor Econ 10(3):719–773
Albert Y (2010) The importance of litigant wealth. DePaul Law Rev 59:2
Alesina A, Drazen A (1991) Why are stabilizations delayed? Am Econ Rev 81(5):1170–1188
Avery CN, Fairbanks A, Zeckhauser RJ (2003) The early admissions game. Harvard University Press, Harvard
Bagwell K (2017) Commitment with private resolve
Banks JS, Sobel J (1987) Equilibrium selection in signaling games. Econometrica 55(3):647–661
Baye MR, Dan K, de Vries CG (2005) Comparative analysis of litigation systems: an auction-theoretic approach. Econ J 115(505):583–601
Bliss C, Nalebuff B (1984) Dragon-slaying and ballroom dancing: the private supply of a public good. J Public Econ 25(1):1–12
Board S, Skrzypacz A (2016) Revenue management with forward-looking buyers. J Polit Econ 124(4):1046–1087
Bobkova N (2020) Asymmetric budget constraints in a first-price auction. J Econ Theory 186:104975
Bulow J, Klemperer P (1999) The generalized war of attrition. Am Econ Rev 89(1):175–189
Campolieti M, Hebdon R, Hyatt D (2005) Strike incidence and strike duration: some new evidence from Ontario. ILR Rev 58(4):610–630
Chatterjee K, Samuelson L (1987) Bargaining with two-sided incomplete information: an infinite horizon model with alternating offers. Rev Econ Stud 54(2):175–192
Dekel E, Jackson MO, Wolinsky A (2007) Jump bidding and budget constraints in all-pay auctions and wars of attrition
Dekel E, Jackson MO, Wolinsky A (2008) Vote buying: general elections. J Polit Econ 116(2):351–380
Dekel E, Jackson MO, Wolinsky A (2009) Vote buying: legislatures and lobbying. Quart J Polit Sci 4(2):103–128
Fanning J (2016) Reputational bargaining and deadlines. Econometrica 84(3):1131–1179
Farrell J, Simcoe T (2012) Choosing the rules for consensus standardization. Rand J Econ 43(2):235–252
Fearon James D (1998) Bargaining, enforcement, and international cooperation. Int Organ 52(2):269–305
Fudenberg D, Tirole J (1986) A theory of exit in duopoly. Econometrica 54(4):943–960
Georgiadis G, Kim Y, Kwon DH (2019) The absence of attrition in the war of attrition under complete information
Hall BH, Moncada-Paternó-Castello P, Montresor S, Vezzani A (2016) Financing constraints, r &d investments and innovative performances: new empirical evidence at the firm level for europe. Econ Innov New Technol 25(3):183–196
Hendricks K, Weiss A, Wilson C (1988) The war of attrition in continuous time with complete information. Int Econ Rev 29(4):663–680
Hörner J, Sahuguet N (2011) A war of attrition with endogenous effort levels. Econ Theor 47(1):1–27
In-Koo C, Kreps David M (1987) Signaling games and stable equilibria. Q J Econ 102(2):179–221
Kambe S (1999) Bargaining with imperfect commitment. Games Econom Behav 28(2):217–237
Kennan J, Wilson R (1989) Strategic bargaining models and interpretation of strike data. J Appl Economet 4(S1):S87–S130
Kornhauser L, Rubinstein A, Wilson C (1989) Reputation and patience in the“war of attrition’’. Economica 56(221):15–24
Kotowski MH, Fei L (2014) On the continuous equilibria of affiliated-value, all-pay auctions with private budget constraints. Games Econom Behav 85:84–108
Kotowski MH, Li F (2014) The war of attrition and the revelation of valuable information. Econ Lett 124(3):420–423
Kreps D, Wilson R (1982) Reputation and imperfect information. J Econ Theory 27(2):253–279
Krishna V, Morgan J (1997) An analysis of the war of attrition and the all-pay auction. J Econ Theory 72(2):343–362
Leininger W (1991) Patent competition, rent dissipation, and the persistence of monopoly: the role of research budgets. J Econ Theory 53(1):146–172
Mas-Colell A, Whinston M, Dennis G, Jerry R et al (1995) Microeconomic theory, vol 1. Oxford University Press, New York
McAfee Preston R (2005) Competitive solutions: the strategists toolkit. Princeton University Press, Princeton
McGuigan James R, Moyer Charles R, Harris FHB (2016) Managerial economics: applications, strategies and tactics, 14th edn. South-Western College Pub, Berlin
Myatt DP (2005) Instant exit from the asymmetric war of attrition
Olszewski W, Siegel R (2016) Large contests. Econometrica 84(2):835–854
Olszewski W, Siegel R (2019) Bid caps in large contests. Games Econom Behav 115:101–112
Ponsati C, Sákovics J (1995) The war of attrition with incomplete information. Math Soc Sci 29(3):239–254
Powell R (2017) Taking sides in wars of attrition. Am Polit Sci Rev 111(2):219–236
Riley John G (1980) Strong evolutionary equilibrium and the war of attrition. J Theor Biol 82(3):383–400
Sanktjohanser A (2017) Optimally stubborn
Schroth E, Szalay D (2010) Cash breeds success: the role of financing constraints in patent races. Rev Finan 14(1):73–118
Siegel R (2009) All-pay contests. Econometrica 77(1):71–92
Skrzypacz A, Fuchs W (2013) Bargaining with deadlines and private information. Am Econ J Microecon 5(4):219–243
Smith Maynard J (1974) The theory of games and the evolution of animal conflicts. J Theor Biol 47(1):209–221
Yeon-Koo C, Gale Ian L (1996) Bottom-fishing and declining prices in sequential auctions. Econ Lett 50(3):373–379
Acknowledgements
The paper was previously circulated under the title “wars of attrition with private resource constraints.” We would like to thank the editor, the associate editor, and the referee for encouragement and very helpful comments. We also thank Paulo Barelli, Tilman Börgers, Jon Eguia, Itay Fainmesser, Hari Govindan, Johannes Hörner, Maciej Kotowski, Jihong Lee, Fei Li, Qingmin Liu, David Miller, Santanu Roy, and seminar participants at CSUF, Michigan, Rochester, Midwest Theory Conferences at SMU and WUSTL, Nanjing International Conference on Game Theory, and 2018 SEA conference for comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix A: Proofs
Appendix A: Proofs
1.1 Proof of Lemma 3.1
For any \(t\ge 2T+2\), only high budget players remain in the game. Since tie-breaking favors player 2, following the argument for the complete information case (in the first paragraph in Section 3.1), 1h concedes in period \(t\ge 2T+3\) and 2h bids in period \(t\ge 2T+2\).
To prove the final part of the lemma, we calculate the continuation payoff \(U^{2h}_{2T}\) of 2h in period 2T. Let \(\beta ^{1h}_{2T+1}\) be the probability with which 1h concedes in \(2T+1\). Then,
where the inequality follows from \(V_2>2\varepsilon \).
1.2 Proof of Proposition 3.3
If \(V_2>B_h\), then it is a dominant strategy for 2h to bid in every period until she depletes her budget. If \(V_2<B_h\), suppose by contradiction that 2h concedes with positive probability in period 2t with \(t\ge 2\). It follows that the posterior belief that player 1 has a high budget in period 2t must be larger than zero, since otherwise it is common knowledge that player 1 has a lower budget than player 2 and following the complete information case player 2 bids for sure. If \(V_2>(T-t+1)\varepsilon \), then 2h obtains a positive payoff by always bidding from period 2t to \(2T+2\), a contradiction.
Suppose \(V_2<(T-t+1)\varepsilon \). If 2h strictly prefers to concede in period 2t, so does 2l; otherwise, 2l obtains a non-negative payoff from bidding in 2t. Since 2h can always follows 2l’s strategy, this means that 2h also obtains a non-negative payoff from bidding in 2t, a contradiction. However, if both 2h and 2l concede in period 2t, then player 1, regardless of her type, bids for sure in period \(2t-1\). This implies that both 2h and 2l concede in period \(2t-2\). Continuing this argument, it follows that 2h and 2l concede in period 2. If 2h is indifferent between conceding and bidding in period 2t, then 2l must also weakly prefer to concede; otherwise 2h can always follow 2l’s strategy and obtain a strictly positive payoff, a contradiction. In addition, whenever 2h bids with positive probability, 2l also does so; otherwise, 2l can profitably deviate to bidding, after which player 1 will concede for sure. The above argument implies that both 2h and 2l’s continuation payoffs from bidding in period 2t are zero. Since from period \(2T+2\) onward 2h obtains a positive continuation payoff whereas 2l obtains zero, on the equilibrium path the game cannot move to period \(2T+2\) with positive probability. This means that player 1, regardless of her types, concedes for sure in some period \(2t'+1\) where \(t'\le T\). Since both 2l and 2h can bid in period \(2t'\), applying backward induction again, on the equilibrium path both 1l and 1h will always concede in every period before \(2t'+1\). However, this implies that both 2l and 2h can win for sure if they bid in 2t, a contradiction. Hence, in any wPBE either both 2h and 2l concede in period 2 or 2h always bids.
1.3 Proof of Proposition 3.5
We prove this statement by backward induction. Without loss of generality, we assume \(V_2<B_h\).Footnote 28 By Lemma 3.1, 2h always bids from period 2T onwards, where \(T=B_l/\varepsilon <B_h/\varepsilon \). This implies that in any equilibrium 2l will not concede for sure in period 2T.Footnote 29 Consequently, the total probability that player 1 concedes in period \(2T+1\), \(\beta ^{1h}_{2t+1}\), is no less than \(\varepsilon /V_2\). Note that the continuation payoff of 2h from bidding in period 2T is strictly positive and is weakly larger than that of 2l.
In period \(2T-2\), suppose 2h concedes with positive probability \(\beta ^{2h}_{2T-2}>0\). If \(\beta ^{2h}_{2T-2}<1\), then 2h is indifferent between bidding and conceding. That is,
where \({\bar{\beta }}_{2T-1}=\rho _{2T-1}\beta ^{1h}_{2T-1}+(1-\rho _{2T-1})\beta ^{1l}_{2T-1}\), and the left-hand side of the equation is 2h’s payoff from bidding in period \(2T-2\). Since \(V_2>2\varepsilon \), we have \({\bar{\beta }}_{2T-1}<1\) and \(\beta ^{1h}_{2T+1}<1\). Then 2l’s payoff from bidding in period \(2T-2\) is
which implies that 2l should concede in period \(2T-2\) in equilibrium. However, if 2l deviates to bidding, player 1’s posterior belief is \(\eta _{2T-1}=1\); consequently, player 1 concedes for sure in period \(2T-1\). Therefore, this is a profitable deviation for 2l. Hence \(\beta ^{2h}_{2T-2}\in (0,1)\) cannot be true in any equilibrium.
Suppose \(\beta ^{2h}_{2T-2}=1\), that is, 2h concedes in period \(2T-2\). Then by the same argument as in the previous paragraph, 2l must also concede in \(2T-2\). Hence, bidding in period \(2T-2\) is off the equilibrium path. Note that for any mixed action of player 1 in subsequent periods that can result a strictly positive payoff for 2l, 2h can also obtain a strictly positive payoff, but not vice versa. Therefore, according to GD1, player 1’s posterior belief in period \(2T-1\) must satisfy \(\eta _{2T-1}=1\). Thus, player 1 concedes for sure in period \(2T-1\). But then it is profitable for both 2l and 2h to bid in period \(2T-2\). That is, \(\beta ^{2h}_{2T-2}\ne 1\) and hence, 2h bids in period \(2T-2\) in any equilibrium. In addition, as in period 2T, 2l will not concede for sure in period \(2T-2\), which in turn implies that player 1 concedes with a probability at least \(\varepsilon /V_2\) in period \(2T-1\). Finally, the continuation payoff of 2h from bidding in period \(2T-2\) is again strictly positive and weakly larger than that of 2l.
Using backwards induction, in period \(2T-\tau \) for any \(\tau =4,6,\ldots ,2T-2\), given that the continuation play must be a wPBE that satisfies GD1, by the same argument as in the previous paragraph, if 2h does not bid for sure then it must be that both types of bidder 2 concedes for sure; consequently, the continuation payoff of 2h is strictly positive and is weakly larger than that of 2l. Since bidder 1’s off-equilibrium path belief after bidder 2 bids in period \(2T-\tau \) must satisfy GD1, it must assign probability one to 2h, in which case both 2l and 2h would deviate to bidding in period \(2T-\tau \). Therefore, 2h bids for sure in period \(2T-\tau \) in any wPBE that satisfies GD1.
1.4 Proof of Proposition 3.6
We proceed backwards and split the proof into six steps.
-
(step 1)
From period \(2T+2\) onwards, there is no private information about budgets and the game ends immediately with 2h winning the prize.
-
(step 2)
In period \(2T+1\), 1h bids if \(-\varepsilon +(1-\eta _{2T+1})V_1>0\), i.e., \(\eta _{2T+1} < \eta ^*_{2T+1}\); 1h concedes if \(\eta _{2T+1} > \eta ^*_{2T+1}\).
-
(step 3)
In period 2T, if \(\eta _{2T} > \eta ^*_{2T}\) or \(\rho _{2T} < \rho ^*_{2T}\), then 2l will bid for sure; if \(\eta _{2T} < \eta ^*_{2T}\) and \(\rho _{2T} > \rho ^*_{2T}\), then 2l will mix between conceding and bidding. For 2l to be indifferent, the posterior belief after bidding, \(\eta _{2T+1}\), must jump to \(\eta ^*_{2T+1}\) by step 2, since 1h must mix in period \(2T+1\).
-
(step 4)
In period \(2T-1\), the analysis is a bit involved since we need to solve for both 1h and 1l’s best reply given the posterior beliefs.
-
(step 4.1)
If \(\eta _{2T-1}>\eta ^*_{2T-1}\), then both 1h and 1l concede. To see this, consider the most favorable case for player 1 with \(\rho _{2T-1}=1(>\rho ^*_{2T-1})\) and \(\eta _{2T-1}=\eta _{2T}<\eta ^*_{2T}\). Since 2h bids and 2l mixes in period 2T, 1h’s payoff from bidding in \(2T-1\) is
$$\begin{aligned} -\varepsilon + \eta _{2T-1}\cdot 0 + (1-\eta _{2T-1}) \left( \beta ^{2l}_{2T} V_1 + (1-\beta ^{2l}_{2T})\cdot 0 \right) , \end{aligned}$$where we use the fact that 2h is indifferent between bidding and conceding in period 2T. From step 3, we know that \(\eta _{2T+1}\) must be equal to \(\eta ^*_{2T+1}\) for 2l to be indifferent between bidding and conceding. Thus, the probability 2l concedes in 2T, \(\beta ^{2l}_{2T}\), must satisfy
$$\begin{aligned} \eta _{2T+1}=\frac{\eta _{2T-1}}{\eta _{2T-1} +(1-\eta _{2T-1})(1-\beta ^{2l}_{2T})}=\eta ^*_{2T+1}, \end{aligned}$$thus, 1h’s payoff from bidding \(-\varepsilon + (1-\eta _{2T-1}) \beta ^{2l}_{2T} V_1\) is negative. Intuitively, player 1 can only gain from bidding when 2l concedes in the next period. If the probability that this occurs is small enough, then the expected benefit cannot recover the cost of bidding.
-
(step 4.2)
If \(\eta _{2T-1}<\eta ^*_{2T-1}\) and \(\rho _{2T-1}>\rho ^*_{2T-1}\), then both 1h and 1l bid. This follows from the fact that 2l will randomize in period 2T and now both types of player 1’s payoff from bidding \(-\varepsilon + (1-\eta _{2T-1}) \beta ^{2l}_{2T} V_1\) is positive.
-
(step 4.3)
If \(\eta _{2T-1}<\eta ^*_{2T-1}\) and \(\rho _{2T-1}<\rho ^*_{2T-1}\), then 1h bids and 1l randomizes between bidding and conceding. To see this, note that the posterior belief \(\rho _{2T}\) must jump to \(\rho ^*_{2T}\) if player 1 bids in period \(2T-1\). Moreover, 2l will randomize in period 2T such that 1l is indifferent in period \(2T-1\), since otherwise either both 1h and 1l strictly prefer to bid, which implies \(\rho _{2T}=\rho _{2T-1}\), or 1l strictly prefers to concede, which implies \(\rho _{2T}=1\), in both cases we will reach contradictions.
-
(step 4.1)
-
(step 5)
Now consider period \(2T-2\). If \(\eta _{2T-2}>\eta ^*_{2T-2}\), then 2l bids since both 1h and 1l concede in the next period. If \(\eta _{2T-2}<\eta ^*_{2T-2}\) and \(\rho _{2T-2}<\rho ^*_{2T-2}\), then 2l also bids since 1l randomizes in period \(2T-1\) such that \(\rho _{2T}\) jumps to \(\rho ^*_{2T}\). If \(\eta _{2T-2}<\eta ^*_{2T-2}\) and \(\rho _{2T-2}\ge \rho ^*_{2T-2}\), then 2l randomizes such that \(\eta _{2T-1}=\eta ^*_{2T-1}\), in which case both 1h and 1l will randomize in period \(2T-1\) such that
$$\begin{aligned} \rho _{2T-1}\beta ^{1h}_{2T-1}+(1-\rho _{2T-1})\beta ^{1l}_{2T-1}=\frac{\varepsilon }{V_2} \end{aligned}$$(2)and
$$\begin{aligned} \frac{\rho _{2T-1}(1-\beta ^{1h}_{2T-1})}{\rho _{2T-1}(1-\beta ^{1h}_{2T-1}) +(1-\rho _{2T-1})(1-\beta ^{1l}_{2T-1})} =\frac{\rho _{2T-1}(1-\beta ^{1h}_{2T-1})}{1-\frac{\varepsilon }{V_2}}\ge \rho _{2T}^*, \end{aligned}$$(3)Footnote 30 where the first equation ensures that 2l is willing to randomize in period \(2T-2\) and the second inequality implies that 2l will randomize in period 2T, which in turn provides incentives for 1h and 1l to randomize in period \(2T-1\). Note that if \(\rho _{2T-1}\in [(1-\varepsilon /V_2)^2,(1-\varepsilon /V_2))\) then one solution to (2) and (3) is \(\beta ^{1h}_{2T-1}=0\) and \(\beta ^{1l}_{2T-1}=(\varepsilon /V_2)/(1-\rho _{2T-1})\in (0,1)\), it is also the unique solution when \(\rho _{2T-1}=(1-\varepsilon /V_2)^2\); if \(\rho _{2T-1}>(1-\varepsilon /V_2)\) then \(\beta ^{1h}_{2T-1}\in (0,1)\).
-
(step 6)
Inducting backwards, in period \(2t-1\) for \(t=1,\ldots ,T-1\), we have the following:
-
If \(\eta _{2t-1}>\eta ^*_{2t-1}\), given that 2l’s concession probability in the next period is less than \(\varepsilon /V_1\) (which is zero if \(\eta _{2t-1}>\eta ^*_{2t}\) or leads to \(\eta _{2t+1}=\eta ^*_{2t+1}\) if \(\eta _{2t-1}<\eta ^*_{2t}\)) and that both 1h and 1l are indifferent between bidding and conceding in period \(2t+1\), it is optimal for both 1h and 1l to concede in period \(2t-1\).
-
If \(\eta _{2t-1}<\eta ^*_{2t-1}\) and \(\rho _{2t-1}>\rho ^*_{2t-1}\), since 2l will randomize in period 2t such that \(\eta _{2t+1}=\eta ^*_{2t+1}\), both 1h and 1l prefer to bid in period \(2t-1\).
-
If \(\eta _{2t-1}<\eta ^*_{2t-1}\) and \(\rho _{2t-1}<\rho ^*_{2t-1}\), then 1l has to randomize in period \(2t-1\) such that \(\rho _{2t}=\rho ^*_{2t}\), which requires 2l to concede in period 2t with probability \(\varepsilon /V_1\) to provide incentive for 1l’s randomization. Moreover, since the updated beliefs about player 2’s type satisfy \(\eta _{2s+1}<\eta ^*_{2s+1}\) for all \(s=t,\ldots ,T\), it follows that 1h’s payoff from bidding is strictly positive. Therefore, 1h bids for sure in period \(2t-1\).
In addition, in period 2t for \(t=1,\ldots , T-2\), we have:
-
If \(\eta _{2t}>\eta ^*_{2t}\), then 2l bids, and in the next period both 1h and 1l concede.
-
If \(\eta _{2t}<\eta ^*_{2t}\) and \(\rho _{2t}<\rho ^*_{2t}\), then 2l bids, and in the next period 1l randomizes such that \(\rho _{2t+2}=\rho ^*_{2t+2}\).
-
If \(\eta _{2t}<\eta ^*_{2t}\) and \(\rho _{2t}\ge \rho ^*_{2t}\), then 2l randomizes such that \(\eta _{2t+1}=\eta ^*_{2t+1}\), and in the next period both 1h and 1l randomize such that
$$\begin{aligned} \rho _{2t+1}\beta ^{1h}_{2t+1}+(1-\rho _{2t+1})\beta ^{1l}_{2t+1}=\frac{\varepsilon }{V_2} \end{aligned}$$and
$$\begin{aligned} \frac{\rho _{2t+1}(1-\beta ^{1h}_{2t+1})}{\rho _{2t+1}(1-\beta ^{1h}_{2t+1}) +(1-\rho _{2t+1})(1-\beta ^{1l}_{2t+1})}\ge \rho _{2t+2}^*. \end{aligned}$$
Hence, on the equilibrium path, if \(\eta _1>\eta ^*_1\), then player 2 wins the prize immediately; if \(\eta _1<\eta ^*_1\) and \(\rho _1<\rho ^*_1\), then 1h always bids, both 1l and 2l concede with positive probabilities in every period; if \(\eta _1<\eta ^*_1\) and \(\rho _1>\rho ^*_1\), then 1h and 1l bid in the first period then randomize in all subsequent periods, and 2l always randomizes in every period. \(\square \)
-
1.5 Proof of Proposition 3.7
Denote the time length of each period by \(dt=\epsilon \). That is, we normalize the instantaneous cost of fighting to be one. In the limit as \(\epsilon \rightarrow 0\), we have \(\eta ^*_1=e^{-\frac{B_l}{V_1}}\) and \(\rho ^*_1=e^{-\frac{B_l}{V_2}}\).
When the game continues after the first instant, player i concedes with a probability \(\frac{\epsilon }{V_{-i}}=\frac{1}{V_{-i}}dt\) in period t. Therefore, in each period t, the probability that at least one player concedes is \(1-(1-\frac{1}{V_{1}}dt)(1-\frac{1}{V_{2}}dt)\rightarrow \lambda dt\), where \(\lambda =\frac{1}{V_1}+\frac{1}{V_2}\). Notice that \(\lambda \) is the Poisson arrival rate of the event that the game ends (with a deadline \(B_l\)). Therefore, conditioning on the game continues after the first instant, the expected length is
Next, we categorize the equilibrium into three cases, based one the concession probabilities in the first instant:
-
(i)
If \(\eta _1<e^{-\frac{B_l}{V_1}}\) and \(\rho _1<e^{-\frac{B_l}{V_2}}\), then in the first instant, player 1 fights with probability \(\frac{\rho _1}{\rho _1^*}=\rho _1e^{\frac{B_l}{V_2}}\). Hence, the expected length is \(\tau =\rho _1e^{\frac{B_l}{V_2}}\tau _W\).
-
(ii)
If \(\eta _1>e^{-\frac{B_l}{V_1}}\) and \(\rho _1<e^{-\frac{B_l}{V_2}}\), then in the first instant, player 2 fights with probability \(\frac{\eta _1}{\eta _1^*}=\eta _1e^{\frac{B_l}{V_1}}\). Hence, the expected length is \(\tau =\eta _1e^{\frac{B_l}{V_1}}\tau _W\).
-
(iii)
If \(\eta _1>e^{-\frac{B_l}{V_1}}\), then both 1h and 1l concedes immediately (by Proposition 3.6), which means that war of attrition ends immediately.
1.6 Proof of Proposition 4.1 and 4.2
For each \(i\in \{1,2\}\), let \(\tau _i(B_i)\le B_i\) denote the concession time for a player with budget \(B_i\in [{\underline{B}},{\bar{B}}]\), where \(\tau _i(\cdot )\) is non-decreasing. For \(t\ge 0\), define \(G_i(t)\equiv \Pr (\{B_i:\tau _i(B_i)\le t\})\) as the probability that player i has conceded by time t when she follows the strategy \(\tau _i\). Finally, assume without loss of generality that \(c_1\le c_2\), that is, \({\bar{B}}/c_1\ge {\bar{B}}/c_2\).
The proof is divided into three steps. First, we show that (i) \(G_1(\cdot )\) is strictly increasing, has no atoms on the interval \([\underline{B},{\bar{B}}c_1/c_2]\), and satisfies \(\min \{t:G_1(t)=1\}={\bar{B}}/c_2\); and (ii) \(G_2(\cdot )\) is strictly increasing, has no atoms on the interval \([\underline{B},{\bar{B}}]\), and satisfies \(\min \{t:G_2(t)=1\}={\bar{B}}/c_2\). That is, \(G_i\) admits a density \(g_i\) for each \(i=1,2\), and we have \(\tau _1(\cdot )\) is strictly increasing on \([\underline{B},{\bar{B}}c_1/c_2]\) and \(\tau _2(\cdot )\) is strictly increasing on \([\underline{B},{\bar{B}}]\). There are four substeps:Footnote 31
-
(1)
\(\tau _1({\bar{B}}c_1/c_2)=\tau _2({\bar{B}})={\bar{B}}/c_2\). If \(\tau _2({\bar{B}})<{\bar{B}}/c_2\), then for a type B player 1 that is close enough to \({\bar{B}}c_1/c_2\), she can profitably deviate to conceding slightly later. If \(\tau _1({\bar{B}}c_1/c_2)<{\bar{B}}/c_2\), then for a type B player 2 that is close enough to \({\bar{B}}\), she can also profitably deviate to conceding slightly later.
-
(2)
There are no jumps in \(G_i(\cdot )\). If there were a jump at some time t, then there will be types who are suppose to concede at t, but they have budgets to wait slightly longer in order to win with a discrete probability, which is a profitable deviation.
-
(3)
There is no interval \((t',t'')\) with \(t''<{\bar{B}}/c_2\) such that \(G_2(\cdot )\) is constant on this interval. If there were such an interval, then those types who concede at (or right after) \(t''\) will prefer to concede at (or right after) \(t'\).
-
(4)
There is no interval \((t',t'')\) with \(t''<{\bar{B}}c_1/c_2\) such that \(G_1(\cdot )\) is constant on this interval. The argument is the same as that in the previous substep.
Next, we show that under the monotone hazard rate condition, there is a unique cutoff budget \(B_i^*\in ({\underline{B}},{\bar{B}})\) such that for any \(B_i<B_i^*\), player i with budget \(B_i\) is indifferent between conceding at any time before she depletes her budget; player i with budget \(B_i>B_i^*\) only concedes after she runs out of budget. Since players’ values are complete information, for a player to concede before depleting her budget, i.e., \(\tau _i(B_i)<B_i/c_i\), she must be indifferent between bidding and conceding at any time between 0 and \(B_i/c_i\). The indifference condition is
where the left-hand side of the equation is the expected benefit from waiting for a length dt of time and the right-hand side is the cost of waiting. Therefore, players’ concession rates are constant if they concede before running out of budget. Since \(\lambda _j(B_j)\) is increasing in \(B_j\), so is \(\tau '_j(B_j)\). That is, \(\tau _j(B_j)\) is increasing and convex for those \(B_j\)’s such that \(\tau _j(B_j)<B_j/c_j\). Since \(\lambda _j(B_j)/\tau '_j(B_j)=g_j(\tau _j(B_j))/(1-G_j(\tau _j(B_j)))\equiv \lambda _{G_j}(\tau _j(B_j))\) and \(\lim _{t\rightarrow \infty }\lambda _{G_j}(t)=\infty \), there exists \(t_j^*\) such that for any \(t>t_j^*\), \(V\lambda _{G_j}(t)>c_i\). Therefore, for a player with a budget close to \({\bar{B}}\), at the time she is depleting her budget she strictly prefers waiting instead of conceding; as a result, she only concedes when she runs out of budget. Moreover, suppose player i with budget \(B_i\) concedes at time \(B_i/c_i\) and \(G_j(\cdot )\) is differentiable at \(B_i/c_i\), then \(\lambda _j(B_j)/\tau '_j(B_j)=\lambda _j(B_j)c_i\). Since \(\lambda _j(B_j)\) is strictly increasing, we have \(V_i\lambda _j(B_j')c_i>c_i\) for all \(B_j'>B_j\), it follows that player i with a budget \(B_i'>B_i\) concedes at time \(B_i'/c_i\). This establishes that there is a cutoff \(B_i^*\) such that \(\tau _i(B_i)=B_i/c_i\) for all \(B_i\ge B_i^*\). The uniqueness of \(B_i^*\) follows directly from the monotone hazard rate assumption.
Finally, we solve the equilibrium in its closed form. From the two indifference conditions
and the boundary conditions \(\tau _1(B_1^*)=B_1^*/c_1=\tau _2(B_2^*)=B_2^*/c_2\), we have
and
There are three cases to consider. (i) If
then \(\tau _1({\underline{B}})=\tau _2({\underline{B}})=0\); moreover, from (4) we have \(B_i^*\) as the unique solution to the equation
for \(i\ne j\). (ii) If
then \(\tau _1({\underline{B}})<\tau _2({\underline{B}})\), which implies that one (and only one) player concedes with a positive probability at time zero. Therefore, we have \(\tau _2({\underline{B}})=0\) and \(B_2^*\) is given by
In addition, we have \(B_1^*=c_1B_2^*/c_2\) and there exists a unique \({\underline{B}}_1\in ({\underline{B}},B_1^*)\) such that \(\tau _1(B_1)=0\) for all \(B_1\in [{\underline{B}},{\underline{B}}_1]\), where \({\underline{B}}_1\) satisfies
(iii) The last case where
is symmetric to the second possibility.\(\square \)
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Huangfu, B., Ghosh, G. & Liu, H. Resource inequality in the war of attrition. Int J Game Theory 52, 33–61 (2023). https://doi.org/10.1007/s00182-022-00809-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-022-00809-0