Minimum cost spanning tree problems as value sharing problems

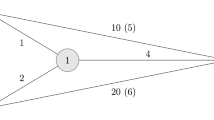
Abstract

Minimum cost spanning tree (mcst) problems study situations in which agents must connect to a source to obtain a good, with the cost of building an edge being independent of the number of users. We reinterpret mcst problems as value sharing problems, and show that the folk and cycle-complete solutions, two of the most studied cost-sharing solutions for mcst problems, do not share values in a consistent way. More precisely, two mcst problems yielding the same value sharing problem might lead to value being shared in different ways. However, they satisfy a weaker version of the property that applies only to elementary problems, in which the cost on an edge can only be 0 or 1. The folk solution satisfies the version related to the public approach, while the cycle-complete solution satisfies the one related to the private approach, which differ depending if we allow a group to use the nodes of other agents or only their own nodes. We then build axiomatizations built on these properties. While the two solutions are usually seen as competitors in the private approach, the results point towards a different interpretation: the two solutions are based on different interpretations of the mcst problem, but are otherwise conceptually very close.

A Appendix: Independence of properties

1.1 A.1 Theorem 2

The cycle-complete solution satisfies Piecewise Linearity, Symmetry and Group Independence, but fails $C^{PUB}$-Cost Equivalence.

$Sh(C^{PUB})$ satisfies $C^{PUB}$-Cost Equivalence, Symmetry and Group Independence, but fails Piecewise Linearity (see Example 1).

Take an order $\pi$ of N. For each $c\in \Gamma ^{e}$ let $y^{\pi }(N,c)$ be the extreme core allocation of $C^{PUB}$ according to $\pi ,$ i.e. we lexicographically maximize among core allocations according to $\pi .$ Let ${\bar{y}}^{\pi }$ be the Piecewise-linear extension of $y^{\pi }.$ ${\bar{y}} ^{\pi }$ satisfies $C^{PUB}$-Core Equivalence, Piecewise Linearity and Group Independence but fails Symmetry.

For each $c\in \Gamma$ let $y^{eq}(N,c)$ be such that $y_{i}^{eq}(N,c)= \frac{C^{PUB}(N,c)}{|N|}$ for all $i\in N.$ $y^{eq}$ satisfies $C^{PUB}$-Core Equivalence, Piecewise Linearity and Symmetry but fails Group Independence.

1.2 A.2 Theorem 3

The folk solution satisfies Piecewise Linearity, Symmetry, Core Selection but not Core Additivity in Values.

The permutation-weighted average of extreme core allocations of C satisfies Core Additivity in Values, Symmetry and Core Selection but not Piecewise Linearity.

Take an order $\pi$ of N. For each $c\in \Gamma ^{e}$ let $x^{\pi }(N,c)$ be the extreme core allocation of C according to $\pi ,$ i.e. we lexicographically maximize among core allocations according to $\pi .$ Let ${\bar{x}}^{\pi }$ be the Piecewise-linear extension of $y^{\pi }.$ ${\bar{x}} ^{\pi }$ satisfies Core Additivity in Values, Piecewise Linearity and Core Selection but not Symmetry.

Take an order $\pi$ of N. For each $c\in \Gamma ^{e}$ let $z^{\pi }(N,c)$ be the extreme core allocation of C according to $\pi ,$ taking into account symmetry, i.e., with the constraint that if i, j are symmetric in c,  $z_{i}^{\pi }=z_{j}^{\pi }.$ Let ${\bar{z}}^{\pi }$ be the piecewise linear extension of $z^{\pi }.$ ${\bar{z}}^{\pi }$ satisfies Piecewise Linearity, Core Selection and Symmetry but not Core Additivity in Values. To see that Core Additivity in Values fails, consider a 4-player example with $c_{01}=c_{02}=c_{13}=c_{23}=c_{34}=0$ and $c_{e}=1$ otherwise. Consider an order $\pi$ such that 3 has priority over 4. Then $z^{\pi }(N,c)=(0,0,-1,1),$ as agents 3 and 4 are not symmetric in c.

Consider $c^{\prime }$ such that $c_{01}^{\prime }=c_{02}^{\prime }=c_{13}^{\prime }=c_{23}^{\prime }=0$ and $c_{e}^{\prime \prime }=1$ otherwise. Then $z^{\pi }(N,c^{\prime })=(0,0,0,1).$

Consider $c^{\prime \prime }$ such that $c_{34}^{\prime \prime }=0$ and $c_{e}^{\prime \prime }=1$ otherwise. Then $z^{\pi }(N,c^{\prime \prime })=(0,0, \frac{1}{2},\frac{1}{2})$ as 3 and 4 are symmetric in $c^{\prime \prime }.$

Notice that $Core(V\left( \cdot ,c\right) )=Core(V\left( \cdot ,c^{\prime }\right) )+Core(V\left( \cdot ,c^{\prime \prime }\right) ).$ But we have that $C(\left\{ i\right\} ,c)-z_{i}^{\pi }(N,c)=1--1=2,$ while $C(\left\{ i\right\} ,c^{\prime })-z_{i}^{\pi }(N,c^{\prime })+C(\left\{ i\right\} ,c^{\prime \prime })-z_{i}^{\pi }(N,c^{\prime \prime })=1-0+1-\frac{1}{2}= \frac{3}{2},$ and thus Core Additivity in Values fails.