Abstract
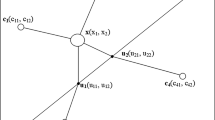
This paper presents a general mixed-norm minisum problem for locating a single facility in continuous space. It is assumed that several transportation modes exist between the new facility and a given set of fixed points (the customers), each mode being represented by a different ℓ p norm. A simple extension of Weiszfeld’s well known iterative procedure is proposed to solve the model. Convergence properties and optimality criteria are derived, and computational results are given.
Similar content being viewed by others
References
Brimberg J (1989) Properties of distance functions and minisum location models. Ph.D. Thesis, McMaster University, Hamilton, Canada
Brimberg J, Love RF (1992) Local convergence in a generalized Fermat–Weber problem. Ann Oper Res 40: 33–66
Brimberg J, Love RF (1993a) Global convergence of a generalized iterative procedure for the minisum location problem with ℓ p distances. Oper Res 41: 1153–1163
Brimberg J, Love RF (1993b) General considerations on the use of the weighted ℓ p norm as an empirical distance measure. Transport Sci 27: 341–349
Brimberg J, Love RF (1995) Estimating distances. In: Drezner Z (eds) Facility location: a survey of applications and methods. Springer, New York
Durier R, Michelot C (1985) Geometrical properties of the Fermat–Weber problem. Eur J Oper Res 20: 332–343
Hansen P, Perreur J, Thisse JF (1980) Location theory, dominance, and convexity: some further results. Oper Res 28: 1241–1250
Juel H, Love RF (1981) Fixed point optimality criteria for the location problem with arbitrary norms. J Oper Res Soc 32: 891–897
Love RF, Morris JG, Wesolowsky GO (1988) Facilities location: models and methods. North-Holland, New York
Planchart A, Hurter AP (1975) An efficient algorithm for the solution of the Weber problem with mixed norms. SIAM J Control 13: 650–665
Rockafellar RT (1970) Convex analysis. Princeton University Press, Princeton
Weiszfeld E (1937) Sur le point lequel la somme des distances de n points donnés est minimum. Tohoku Math J 43: 355–386
Witzgall CJ (1964) Optimal location of a central facility: mathematical models and concepts. National Bureau of Standards report 8388, US Department of Commerce, Washington DC, USA
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Brimberg, J., Love, R. & Mladenović, N. Extension of the Weiszfeld procedure to a single facility minisum location model with mixed ℓ p norms. Math Meth Oper Res 70, 269–283 (2009). https://doi.org/10.1007/s00186-008-0268-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-008-0268-z