Abstract
This paper focuses on numerical evaluation techniques related to fluctuation theory for Lévy processes; they can be applied in various domains, e.g., in finance in the pricing of so-called barrier options. More specifically, with \(\bar{X}_t:= \sup _{0\le s\le t} X_s\) denoting the running maximum of the Lévy process \(X_t\), the aim is to evaluate \(\mathbb{P }(\bar{X}_t \in \mathrm{d}x)\) for \(t,x>0\). The starting point is the Wiener–Hopf factorization, which yields an expression for the transform \(\mathbb E e^{-\alpha \bar{X}_{e(\vartheta )}}\) of the running maximum at an exponential epoch (with \(\vartheta ^{-1}\) the mean of this exponential random variable). This expression is first rewritten in a more convenient form, and then it is pointed out how to use Laplace inversion techniques to numerically evaluate \(\mathbb{P }(\bar{X}_t\in \mathrm{d}x).\) In our experiments we rely on the efficient and accurate algorithm developed in den Iseger (Probab Eng Inf Sci 20:1–44, 2006). We illustrate the performance of the algorithm with various examples: Brownian motion (with drift), a compound Poisson process, and a jump diffusion process. In models with jumps, we are also able to compute the density of the first time a specific threshold is exceeded, jointly with the corresponding overshoot. The paper is concluded by pointing out how our algorithm can be used in order to analyze the Lévy process’ concave majorant.

Similar content being viewed by others
References
Abate J, Whitt W (1995) Numerical inversion of laplace transforms of probability distributions. ORSA J Comput 7:36–43
Asghari N, den Iseger P, Mandjes M (2012) Numerical techniques in Lévy fluctuation theory. Meth Comp Appl Probab, to appear
Asmussen S, Nerman O, Olsson M (1996) Fitting phase-type distributions via the EM algorithm. Scand J Stat 23:419–441
Asmussen S, Avram F, Pistorius M (2004) Russian and American put options under exponential phase-type Lévy models. Stoch Proc Appl 109:79–111
Asmussen S, Madan D, Pistorius M (2007) Pricing equity default swaps under an approximation to the CGMY Lévy model. J Comput Finance 11:79–93
Bertoin J (1998) Lévy Processes. Cambridge University Press, Cambridge
Carolan C, Dykstra R (2003) Characterization of the least concave majorant of Brownian motion, conditional on a vertex point, with application to construction. Ann Inst Stat Math 55:487–497
Carr P, Geman H, Madan D, Yor M (2003) Stochastic volatility for Lévy processes. Math Finance 13:345–382
Cooley J, Tukey J (1965) An algorithm for the machine calculation of complex Fourier series. Math Comput 19:297–301
Cont R, Tankov P (2003) Financial modelling with jump processes. Chapman & Hall/CRC Press, Boca Raton
den Iseger P (2006) Numerical transform inversion using Gaussian quadrature. Probab Eng Inf Sci 20:1–44
den Iseger P, Oldenkamp E (2006) Pricing guaranteed return rate products and discretely sampled asian options. J Comput Finance 9:1–39
Dubner H, Abate J (1968) Numerical inversion of Laplace transforms by relating them to the finite Fourier cosine transform. J ACM 15:115–123
Groeneboom P (1983) The concave majorant of brownian motion. Ann Probab 11:1016–1027
Gruntjes P, den Iseger P, Mandjes M (2012) Numerical techniques in Lévy fluctuation theory: the small-jumps case. Forthcoming
Harrison J (1985) Brownian motion and stochastic flow systems. Wiley, New York
Hazewinkel M (ed) (2001) Wiener-Hopf method. Encyclopaedia of mathematics. Springer, Berlin
Kyprianou A (2006) Introductory lectures on fluctuations of Lévy processes with applications. Springer, Berlin
Lewis A, Mordecki E (2008) Wiener-Hopf factorization for Lévy processes having positive jumps with rational transforms. J Appl Probab 45:118–134
Nguyen-Ngoc L, Yor M (2002) Exotic options and Lévy processes. In: Aït Sahalia Y, Hansen LP (eds) Handbook of financial econometrics. North Holland, Amsterdam
Pecherskii E, Rogozin B (1969) On the joint distribution of random variables associated with fluctuations of a process with independent increments. Theory Probab Appl 14:410–423
Rogers L (2000) Evaluating first-passage probabilities for spectrally one-sided Lévy processes. J Appl Probab 37:1173–1180
Surya B (2008) Evaluating scale functions of spectrally negative Lévy processes. J Appl Probab 45:135–149
Author information
Authors and Affiliations
Corresponding author
Additional information
Date: February 25, 2013. MM is also with Eurandom, Eindhoven, the Netherlands, and CWI, Amsterdam, the Netherlands.
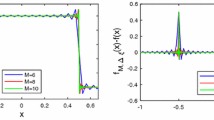
Appendix: Numerical output
Appendix: Numerical output
Rights and permissions
About this article
Cite this article
Iseger, P.D., Gruntjes, P. & Mandjes, M. A Wiener–Hopf based approach to numerical computations in fluctuation theory for Lévy processes. Math Meth Oper Res 78, 101–118 (2013). https://doi.org/10.1007/s00186-013-0434-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-013-0434-9