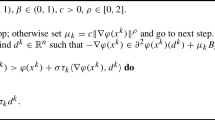Skip to main content
Springer Nature Link
Log in

Nonsingularity in matrix conic optimization induced by spectral norm via a smoothing metric projector

  • Original Article
  • Published:
Mathematical Methods of Operations Research Aims and scope Submit manuscript

Abstract

Matrix conic optimization induced by spectral norm (MOSN) has found important applications in many fields. This paper focus on the optimality conditions and perturbation analysis of the MOSN problem. The Karush–Kuhn–Tucker (KKT) conditions of the MOSN problem can be reformulated as a nonsmooth system via the metric projector over the cone. We show in this paper, the nonsingularity of the Clarke’s generalized Jacobian of the smoothing KKT system constructed by a smoothing metric projector, the strong regularity and the strong second-order sufficient condition under constraint nondegeneracy are all equivalent. Moreover, this nonsingularity is used in several globally convergent smoothing Newton methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Bonnans JF, Ramirez CH (2005) Perturbation analysis of second-order cone programming problems. Math Program Ser B 104:205–227

    Article  MATH  Google Scholar 

  • Bonnans JF, Shapiro A (2000) Perturbation analysis of optimization problems. Springer, New York

    MATH  Google Scholar 

  • Chen CH (2012) Numerical algorithms for a class of matrix norm approximation problems. PhD thesis, Nanjing University

  • Chan ZX, Sun DF (2008) Constraint nondegeneracy, strong regularity and nonsingularity in semidefinite programming. SIAM J Optim 19:370–396

    Article  MathSciNet  MATH  Google Scholar 

  • Clarke FH (1976) On the inverse function theorem. Pac J Math 64:97–102

    Article  MATH  Google Scholar 

  • Ding C (2010) An introduction to a class of matrix optimization problem, PhD thesis, National University of Singapore, Singapore

  • Ding C, Sun DF, Toh KC (2010) An introduction to a class of matrix cone programming. Math Program, to appear

  • Facchinei F, Pang JS (2003) Finite-dimensional variational inequalities and complementarity problems: volume I, volumn II. Springer, New York

    Google Scholar 

  • Horn R, Johnson C (1985) Matrix analysis. Cambridge University Press, Cambridge, MA

    Book  MATH  Google Scholar 

  • Lewis AS, Sendov HS (2005) Nonsmooth analysis of singular values, II. Applications. Set-valued Anal 13:243–264

    Article  MathSciNet  MATH  Google Scholar 

  • Qi LQ, Sun DF, Zhou GL (2000) A new look at smoothing Newton methods for nonlinear complementarity problems and box constrained variational inequalities. Math Program Ser A 87:1–35

    MathSciNet  MATH  Google Scholar 

  • Robinson SM (1976) First order conditions for general nonlinear optimization. SIAM J Appl Math 30:597–607

    Article  MathSciNet  Google Scholar 

  • Robinson SM (1980) Strongly regular generalized equations. Math Oper Res 5:43–62

    Article  MathSciNet  MATH  Google Scholar 

  • Sun DF (2006) The strong second order sufficient condition and constraint nondegeneracy in nonlinear semidefinite programming and their implications. Math Oper Res 31:761–776

    Article  MathSciNet  MATH  Google Scholar 

  • Sun J, Sun DF, Qi LQ (2004) A squared smoothing Newton method for nonsmooth matrix equations and its applications in semidefinite optimization problems. SIAM J Optim 14:783–806

    Article  MathSciNet  MATH  Google Scholar 

  • Wang Y, Zhang LW (2010) Nonsingularity in second-order cone programming via the smoothing metric projector. Sci China Ser A 53(4):1025–1038

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The authors thank the referees for their careful reading of the paper and helpful suggestions.

Author information

Authors and Affiliations

  1. Institute of Operations Research and Control Theory, School of Mathematical Sciences, Dalian University of Technology, Dalian, 116024 , China

    Liwei Zhang, Shaoyan Guo & Jia Wu

  2. Institute of Advanced Control Technology, School of Control Science & Engineering, Dalian University of Technology, Dalian, 116024 , China

    Shoulin Hao

Authors
  1. Liwei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Shaoyan Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jia Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Shoulin Hao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jia Wu.

Additional information

Supported by the National Natural Science Foundation of China under Projects No. 11071029 and No. 91130007, and the Fundamental Research Funds for the Central Universities under project No. DUT12RC(3)51.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, L., Guo, S., Wu, J. et al. Nonsingularity in matrix conic optimization induced by spectral norm via a smoothing metric projector. Math Meth Oper Res 78, 373–404 (2013). https://doi.org/10.1007/s00186-013-0449-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00186-013-0449-2

Keywords