Inventory control and pricing for perishable products under age and price dependent stochastic demand

Abstract

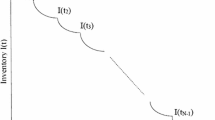
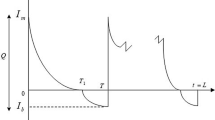
Perishable products have a short lifetime and cause a high amount of wastage when managed ineffectively, due to their deterioration over time. We consider coordinated inventory and pricing decisions for perishable products in a periodically-reviewed inventory system with an age and price dependent random demand. We consider the products with a fixed shelf lifetime and use dynamic programming to model this system. We prove certain structural characteristics of the optimal solution and also analyze the effect of different parameters on the optimal solution through numerical experiments. In addition, we analyze simple-to-implement inventory control policies, namely quantity-based and age-based policies, and investigate their effectiveness.

Appendix

1.1 Proof of Proposition 1

In any state (q, t), we should choose an ordering size, Q(q, t), that maximizes $-K-cQ(q,t)+sq+f_c(Q(q,t),m)$ and the maximizer value will be independent of q and t. So, we can simply say that the optimal order size is same for all q and t values.

1.2 Proof of Proposition 2

Note that the maximum time before ordering a new batch is m periods since it is the maximum life of the product. In our model, we may not wait until the end of m periods and we can make a replenishment before that time. If we neglect the replenishment opportunities before m periods and assume that we make replenishments in every m periods, then the problem turns into a newsvendor problem in which the demand is the total demand of m periods. Hence, it is obvious that the optimal ordering size for our model is always less than the optimal ordering quantity of this newsvendor problem. If we assume that we have a standard newsvendor problem where the demand is equal to the total demand of m periods in our model, we know that the optimal ordering quantity for the newsvendor problem is equal to

$$\begin{aligned} min \Big \{ Q | F^{-1}_{m}(Q) \ge \frac{p-c}{p-s}\Big \} \end{aligned}$$

Thus, the optimal ordering size of the newsvendor problem stated above is an upper-bound for $Q^*$ in our problem.

Similarly, if we assume that we have another newsvendor problem in which the demand is equal to the demand of the first period in our model (where the remaining shelf lifetime is equal to m), the optimal ordering size for this newsvendor problem stated as below, will be a lower bound for $Q^*$ in our problem.

$$\begin{aligned} min \Big \{ Q | F^{-1}_{1}(Q) \ge \frac{p-c}{p-s}\Big \} \end{aligned}$$

1.3 Proof of Lemma 1

We can write the Bellman’s equation in 3.1 as $h=T(h)$ where T is an appropriate transformation function for the vector h. We prove that $h(q+1,t)\ge h(q,t)$ by showing that the transformation function used in the DP equation 3.1 preserves the monotonicity of the function h as stated in the equation below.

$$\begin{aligned} \Pi ^*+h(q,t)= & {} \max \Bigg \{\max _Q\big \{-K-cQ+sq+f_c(Q,m)\big \}, p\,E_D\nonumber \\&\Big [\min \big \{q,D(p,t)\big \}\Big ]+\,E_D\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]\Bigg \}\nonumber \\\le & {} \max \Bigg \{\max _Q\{-K-cQ+s(q+1)+f_c(Q,m)\},\nonumber \\&p\,E_D \Big [\min \big \{q+1,D(p,t)\big \}\Big ]\nonumber \\&+\,E_D\bigg [h\Big (\big [q+1-D(p,t)\big ]^+,t-1\Big )\bigg ]\Bigg \} = \Pi ^*+h(q+1,t)\nonumber \\ \end{aligned}$$

(9.1)

In the above inequality, it can be easily seen that the second line is greater than the first line due to the assumption that $h(q+1,t)\ge h(q,t)$. As a result, we can say that the transformation function T given in the DP equation 3.1 preserves the monotonicity assumption that $h(q+1,t)\ge h(q,t)$ and thus it is proved that h(q, t) is non-decreasing in q for any given t.

For the second part of the Lemma, observe that each product at hand will either be sold at price $p>s$ or salvaged at price s at the end of the period, if not sold until that time. Thus, the value of having 1 more product on hand now is at least s and at most p.

$$\begin{aligned} s \le h(q+1,t)-h(q,t) \le p \end{aligned}$$

(9.2)

1.4 Proof of Lemma 2

We need to show that $h(q,t+1) \ge h(q,t)$ for any q and t. First, note that $\Pi ^*+ h(q,t)=\max \Big \{f_c(q,t), f_o(q)\Big \}$ and $f_o(q)$ is independent of t. Thus it is enough just to show that $f_c(q,t+1) \ge f_c(q,t)$. To prove this statement, we use a sample path argument. Using the sample path argument, we assume that we have two sets of products:

• Set 1: q products in inventory with $t+1$ remaining shelf lifetime

• Set 2: q products in inventory with t remaining shelf lifetime

Now, consider the case when the same customer arrives to these two sets and decides to buy or not a product. Three cases can happen in this system:

• Case I: Customer decides not to buy from both sets

• Case II: Customer decides to buy in both sets

• Case III: Customer decides to buy from set 1 and not to buy from set 2

Note that, it is not possible for the customer to buy from set 2 but not from set 1 because we assume that the customers always prefer fresher products and set 1 has fresher products than set 2 and they both have the same price. So, at a certain day after all customers visit the market, three cases can happen:

• Case 1: All products in both sets are sold out (the number of customers that decide to buy are more than q for both sets)

• Case 2: k number of products are sold in both conditions ($k \le q$)

• Case 3: k number of products are sold from set 1 and m number of products are sold from set 2, ($m \le k \le q$)

Now, using induction we will show that in all these three cases $h(q,t+1) \ge h(q,t)$ for any q and t values.

First for the boundary condition, for $t=0$,

• $h(q,1)=\max \Big \{f_c(q,1), f_o(q)\Big \}-\Pi ^*$

• $h(q,0)=f_o(q)-\Pi ^*$

So, it is obvious that $h(q,1) \ge h(q,0)$ (in all cases)

For $t \ge 1$, using the induction assumption that $h(q,t) \ge h(q,t-1)$

Case 1:

• $f_c(q,t+1) = pq+h(0,t)$ where $h(0,t)=f_o(0)-\Pi ^*$

• $f_c(q,t) = pq+h(0,t-1)$ where $h(0,t-1)=f_o(0)-\Pi ^*$

• So, $h(q,t+1) \ge h(q,t)$

Case 2:

• $f_c(q,t+1) = pk+h(q-k,t)$

• $f_c(q,t) = pk+h(q-k,t-1)$

Due to the induction assumption that $h(q-k,t)\ge h(q-k,t-1)$, we can state that $f_c(q,t+1) \ge f_c(q,t)$ for any q and t.

Case 3:

• $f_c(q,t+1) = pk+h(q-k,t)$

• $f_c(q,t)= pm+h(q-m,t-1)$

$f_c(q,t+1)-f_c(q,t)=p(k-m)+h(q-k,t)-h(q-m,t-1)\ge p(k-m)+h(q-k,t)-h(q-m,t)$ due to the induction assumption that $h(q-m,t)\ge h(q-m,t-1)$.

Now, we note the following inequality, since each product at hand will be sold or salvaged until the end of the period and thus the value of having k more products on hand now is at least sk and at most pk.

$$\begin{aligned} sk \le h(q+k,t)-h(q,t) \le pk \end{aligned}$$

(9.3)

Then, due to the above inequality, we have $s(k-m) \le h(q-m,t)-h(q-k,t) \le p(k-m)$. Thus, $p(k-m)+h(q-k,t)-h(q-m,t) \ge 0$ and we have $f_c(q,t+1)-f_c(q,t)\ge 0$.

As a result, we can say that in all three cases $h(q,t+1) \ge h(q,t)$ for any q and t and we can conclude that h(q, t) is non-decreasing in t for any q value.

1.5 Proof of Proposition 3

If we decide to order, the profit will be $f_o(q)$ that is an increasing function of q with the slope of s. On the other hand, if we decide to continue, the profit will be $f_c(q,t)$ that is again an increasing function of q. Since, a product in inventory will be sold or salvaged at the end, each product will have either a value of p or s for the system. So, it means that $s<f_c(q+1,t)-f_c(q,t)<p$. Hence, $f_c(q,t)$ is increasing with respect to q with a slope higher than s for all q and t. Since, $f_c(0,t)<f_o(0)$ and $f_c(q,t)$ is increasing with a faster rate than $f_o(q)$ for all q and t, $f_c(q,t)$ and $f_o(q)$ will intersect at a single point q for any t and we label it as q(t).

$f_o(q)$ function is independent of t and $f_c(q,t)$ is non-decreasing in remaining shelf lifetime value, t. So, by increasing t, the intersection point will happen at a lower q value meaning that q(t) is non-increasing in t.

1.6 Proof of Proposition 4

We know that $f_o(q)$ is independent of t and $f_c(q,t)$ is non-decreasing in t due to Lemma 2. So for a given q value, $f_o$ and $f_c(t)$ will have exactly one intersection point, denoted as t(q). Hence, t(q) is the critical value for any q such that we should give an order if $t<t(q)$ and do not order if $t\ge t(q)$.

It is obvious that q(t) and t(q) show the same curve for ordering states. In other words $t(q(t))=t$.

We proved in Proposition 3 that q(t) is non-increasing in t. So, for any $t_1\ge t_2$, $q(t_1)\le q(t_2)$. Let $q_1=q(t_1)$ and $q_2=q(t_2)$. Then, since $t_1=t(q(t_1))$ and $t_2=t(q(t_2))$, we can equivalently write that $t_1=t(q_1)$ and $t_2=t(q_2)$. Since $t_1\ge t_2$, $t(q_1)\ge t(q_2)$ for $q_1\le q_2$, which means that t(q) is non-increasing in q.

1.7 Proof of Lemma 3

Let’s assume that a given price p is applied at state (q, t) and define $f_c(q,t,p)=p\,E\Big [\min \big \{q,D(p,t)\big \}\Big ]+E\bigg [h\Big (\big [q-D(p,t)\big ]^+,t-1\Big )\bigg ]$. Also, let $\Pi ^*+ h(q,t,p)=\max \Big \{f_c(q,t,p), f_o(q)\Big \}$. Then, observe that $f_c(q,t)=\max _{p}\{f_c(q,t,p)\}$ and $h(q,t)=\max _{p}\{h(q,t,p)\}$.

Let $p_1$ denote the optimal price at state (q, t) and $p_2$ denote the optimal price at state $(q+1,t)$, such that $h(q,t)=h(q,t,p_1)$ and $h(q+1,t)=h(q+1,t,p_2)$. Now, assume that, the same price $p_1$ is applied at both states (q, t) and $(q+1,t)$, even though it is not the optimal price for state (q+1,t). Note that $h(q+1,t,p_2)\ge h(q+1,t,p_1)$ since $p_2$ is the optimal price at state $(q+1,t)$. Observe that, under the same price $p_1$, due to Lemma 1, $h(q+1,t,p_1)\ge h(q,t,p_1)$. Then $h(q+1,t)=h(q+1,t,p_2)\ge h(q+1,t,p_1)\ge h(q,t,p1)=h(q,t)$. As a result, h(q, t) is non-decreasing in q for any given t, even though the prices are different at different states.

1.8 Proof of Lemma 4

Similar to the previous case, let $p_1$ denote the optimal price at state (q, t) and $p_2$ denote the optimal price at state $(q,t+1)$, such that $h(q,t)=h(q,t,p_1)$ and $h(q,t+1)=h(q,t+1,p_2)$. Now, assume that, the same price $p_1$ is applied at both states (q, t) and $(q,t+1)$, even though it is not the optimal price for state (q, t + 1). Note that $h(q,t+1,p_2)\ge h(q,t+1,p_1)$ since $p_2$ is the optimal price at state $(q,t+1)$. Observe that, under the same price $p_1$, due to Lemma 2, $h(q,t+1,p_1)\ge h(q,t,p_1)$. Then $h(q,t+1)=h(q,t+1,p_2)\ge h(q,t+1,p_1)\ge h(q,t,p1)=h(q,t)$. As a result, h(q, t) is non-decreasing in t for any given q, even though the prices are different at different states.

1.9 Proof of Proposition 7

If we decide to order, the profit will be $f_o(q)$ that is an increasing function of q with the slope of s. On the other hand, if we decide to continue, even though the prices at different states are different, the minimum price still needs to be more than the salvage value s. Since Lemma 1 also applies under dynamic pricing, the profit $f_c(q,t)$ is again an increasing function of q with a slope that is at least equal to s, i.e. $s \le f_c(q+1,t)-f_c(q,t)$. Hence, $f_c(q,t)$ is increasing with respect to q with a slope higher than s for all q and t. Since, $f_c(0,t)<f_o(0)$ and $f_c(q,t)$ is increasing with a faster rate than $f_o(q)$ for all q and t, $f_c(q,t)$ and $f_o(q)$ will again intersect at a single point q for any t and we label it as q(t).

Again, observe that the function $f_o(q)$ is independent of t and $f_c(q,t)$ is non-decreasing in remaining shelf lifetime value, t due to Lemma 2. So, by increasing t, the intersection point will happen at a lower q value meaning that q(t) is non-increasing in t.

1.10 Proof of Proposition 8

We know that $f_o(q)$ is independent of t and $f_c(q,t)$ is non-decreasing in t due to Lemma 2, even though different prices are applied at different states. So for a given q value, $f_o$ and $f_c(t)$ will have exactly one intersection point, denoted as t(q). Hence, t(q) is the critical value for any q such that we should give an order if $t<t(q)$ and do not order if $t\ge t(q)$.

It is obvious that q(t) and t(q) show the same curve for ordering states. In other words: $t(q(t))=t$.

We proved in Proposition 7 that q(t) is non-increasing in t. So, for any $t_1\ge t_2$, $q(t_1)\le q(t_2)$. Let $q_1=q(t_1)$ and $q_2=q(t_2)$. Then, since $t_1=t(q(t_1))$ and $t_2=t(q(t_2))$, we can equivalently write that $t_1=t(q_1)$ and $t_2=t(q_2)$. Since $t_1\ge t_2$, $t(q_1)\ge t(q_2)$ for $q_1\le q_2$, which means that t(q) is non-increasing in q.