Virtual allocation policies for many-server queues with abandonment

Abstract

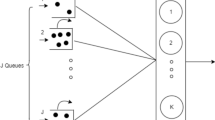
We study a multiclass many-server queueing system with renewal arrivals and generally distributed service and patience times under a nonpreemptive allocation policy. The status of the system is described by a pair of measure-valued processes to track the residual service and patience times of customers in each class. We establish fluid approximations and study the long-term behavior of the fluid model. The equilibrium state of the fluid model leads to a nonlinear program, which enables us to identify a lower bound for the long-run expected total holding and abandonment costs and design an allocation policy to achieve this lower bound. The optimality of the proposed policy is also demonstrated via numerical experiments.

Appendices

Appendix

Lemmas for the Proof of Proposition 1

Consider the following optimization problem where the constraint is perturbed by a small amount $\kappa _i$ for each $i\in \mathscr {I}$,

$$\begin{aligned} \begin{aligned} \text {minimize }\quad&\sum _{i\in \mathscr {I}} [c_iq_i +\gamma _i(\lambda _i-z_i\mu _i)]\\ \text {subject to}\quad&\lambda _iH_i(q_i)=z_i\mu _i+\kappa _i, ~\sum _{i\in \mathscr {I}} z_i\le 1, ~z_{i},q_{i}\ge 0. \end{aligned} \end{aligned}$$

(107)

We use this problem to perform a sensitivity analysis for the optimization problem (33). Let $\kappa =(\kappa _1,\ldots ,\kappa _I)$ and denote by $V^*_{\kappa }$ the optimal value of (107).

Lemma A.1

(Sensitivity Analysis) For any $\varepsilon >0$ there exists a $\delta >0$ such that $V^*_{\kappa }\ge V^*-\varepsilon$ for all $\kappa$ satisfying $\max _i|\kappa _i|\le \delta$.

Proof

Since the patience time distribution is strictly increasing following Assumption 1, the function $H_i(\cdot )$ defined by (32) is continuous and strictly decreasing on its support $[0,\lambda _iN_{F_i}]$ due to (34). So there exists a continuous inverse function $H_i^{-1}(\cdot )$. Therefore we can rewrite (33) and (107) as

$$\begin{aligned} \begin{aligned} \text {minimize }\quad&V({z}) =\sum _{i\in \mathscr {I}} [c_iH_i^{-1}(\frac{{z_i}\mu _i}{\lambda _i}) +\gamma _i(\lambda _i-z_i\mu _i)]\\ \text {subject to}\quad&\sum _{i\in \mathscr {I}} z_i\le 1, ~z_i\mu _i\le \lambda _i, ~ z_{i}\ge 0, \end{aligned} \end{aligned}$$

(108)

and

$$\begin{aligned} \begin{aligned} \text {minimize }\quad&V_{\kappa }({z}) =\sum _{i\in \mathscr {I}} [c_iH_i^{-1}(\frac{{z_i}\mu _i}{\lambda _i} +\frac{\kappa _i}{\lambda _i})+\gamma _i(\lambda _i-z_i\mu _i)]\\ \text {subject to}\quad&\sum _{i\in \mathscr {I}} z_i\le 1, ~0\le z_i\mu _i+\kappa _i\le \lambda _i, ~z_{i}\ge 0. \end{aligned} \end{aligned}$$

(109)

Suppose $N_{F_i}<\infty$ for all $i\in \mathscr {I}$. By (32), $H_i^{-1}(\cdot )$ is continuous on [0, 1] (thus also uniformly continuous) for all $i\in \mathscr {I}$. Denote by ${z}^*({\kappa })$ the optimal solution to (109). Then we can find a corresponding $z^\dagger$ in the feasible region of (108) such that $\max |{z}_i^*({\kappa })-z_i^\dagger |\le \max |\kappa _i|/\mu _i$. So for any $\varepsilon >0$ there exists a $\delta >0$ such that

$$\begin{aligned} |V_{\kappa }(z^*(\kappa ))-V(z^\dagger )|\le \varepsilon , \end{aligned}$$

for all $\kappa$ with $\max |\kappa _i|\le \delta$. Since $V(z^\dagger )\ge V^*$, the above inequality immediately implies

$$\begin{aligned} V^*_{\kappa }\ge V^*-\varepsilon . \end{aligned}$$

(110)

Suppose $N_{F_{i'}}=\infty$ for some $i'\in \mathscr {I}$. This implies that $H^{-1}_{i'}(0)=\infty$. Thus, $H^{-1}_{i'}(\cdot )$ is no longer continuous at the origin. The main idea in dealing with this case is to shrink the feasible region of (108) and (109) by pushing $z_{i'}$ and $z_{i'}\mu _{i'}+\kappa _{i'}$ away from the lower bound 0 without affecting the optimal value. To this end, we choose $z_i^\ddagger =\min \{\frac{\lambda _i}{2\mu _i}\}\wedge \frac{1}{I}$ for all $i\in \mathscr {I}$. It’s easily seen that $z^\ddagger :=(z_1^\ddagger ,\ldots ,z_I^\ddagger )$ is a feasible solution to (108). And there exists a $\delta '>0$ such that $0<z_i^\ddagger \mu _i+\kappa _i<\lambda _i$, $i\in \mathscr {I}$, for all $\kappa$ with $\max |\kappa _i|\le \delta '$. So $z^\ddagger$ is also a feasible solution to (109). Thus we can choose a large enough $M>0$ such that $V(z^*)\le V(z^\ddagger )\le M$ and $V_\kappa (z^*(\kappa ))\le V_{\kappa }(z^\ddagger )\le M$ for all $\kappa$ satisfying $\max |\kappa _i|\le \delta '$. According to the fact that $H_{i'}^{-1}(\cdot )$ is decreasing we can conclude that there exists $\gamma >0$ (depending on M) such that

$$\begin{aligned} z_{i'}^*\ge \gamma \quad \text {and}\quad z_{i'}^*(\kappa )\mu _{i'}+\kappa _{i'}\ge \gamma . \end{aligned}$$

Now let $|\kappa _{i'}|\le \min \{\gamma /2,\delta '\}$, the last inequality implies

$$\begin{aligned} z_{i'}^*(\kappa )\ge \frac{\gamma }{2\mu _{i'}}. \end{aligned}$$

Borrowing the idea from the cutting-plane method, we can update the corresponding constraints for the $i'$th class in (108) and (109) with $z_{i'}\ge \min \{\gamma , \frac{\gamma }{2\mu _{i'}}\}$ and $z_{i'}\mu _{i'}+\kappa _{i'}\ge \gamma$ for all $\kappa$ satisfying $\max |\kappa _i|\le \delta '$ and $|\kappa _{i'}|\le \min \{\gamma /2,\delta '\}$. Then $H^{-1}_{i'}(\cdot )$ again is uniformly continuous on the updated feasible region. So we can apply the same argument as that for the case of $N_{F_i}<\infty$ for all $i\in \mathscr {I}$ to prove the result (110) still holds. $\square$

Lemma A.2

Given Assumptions 1 and 2, for any policy $\bar{\pi }\in \bar{\varPi }$, the following limits hold for all $i\in \mathscr {I}$

$$\begin{aligned}&\lim _{T\rightarrow \infty } \left| \frac{1}{T}\bar{A}_i(T) -\mu _i\frac{1}{T}\int _0^T\bar{Z}_i(s)ds\right| =0, \end{aligned}$$

(111)

$$\begin{aligned}&\lim _{T\rightarrow \infty } \left| \frac{1}{T}\bar{S}_i(T) -\mu _i\frac{1}{T}\int _0^T\bar{Z}_i(s)ds\right| =0, \end{aligned}$$

(112)

$$\begin{aligned}&\lim _{T\rightarrow \infty } \left| \frac{1}{T}\bar{L}_i(T) -\left( \lambda _i-\mu _i\frac{1}{T}\int _0^T\bar{Z}_i(s)ds\right) \right| =0. \end{aligned}$$

(113)

Proof

Obviously, for any $\varepsilon >0$ there exists a $T_0>0$ such that

$$\begin{aligned} |\bar{\mathscr {Z}}_i(0)(C_t)|\le \varepsilon \quad \text {for all }t\ge T_0. \end{aligned}$$

Combining the above with the renewal theorem yields

$$\begin{aligned} \frac{1}{t}\int _0^{t-T_0} \bar{\mathscr {Z}}_i(0)(C_{t-s})dM_{{G_i}}(s) \le \varepsilon \mu _i \quad \text {as }t\rightarrow \infty . \end{aligned}$$

(114)

Therefore

$$\begin{aligned}&\limsup _{t\rightarrow \infty } \frac{1}{t}\int _0^{t} \bar{\mathscr {Z}}_i(0)(C_{t-s})dM_{{G_i}}(s)\\&\quad = \limsup _{t\rightarrow \infty } \frac{1}{t}\int _0^{t-T_0} \bar{\mathscr {Z}}_i(0)(C_{t-s})dM_{{G_i}}(s) +\limsup _{t\rightarrow \infty } \frac{1}{t}\int _{t-T_0}^t \bar{\mathscr {Z}}_i(0)(C_{t-s})dM_{{G_i}}(s)\\&\quad \le \varepsilon \mu _i + \limsup _{t\rightarrow \infty } \frac{1}{t}\int _{t-T_0}^t dM_{{G_i}}(s)\\&\quad =\varepsilon \mu _i, \end{aligned}$$

where the inequality follows from (114) and the fact $\bar{\mathscr {Z}}_i(0)(C_t)\le 1$. Since $\varepsilon$ can be arbitrarily close to 0, we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t}\int _0^t \bar{\mathscr {Z}}_i(0)(C_{t-s})dM_{{G_i}}(s) =0. \end{aligned}$$

(115)

Since $G_i$ has a directly integrable density $g_i$ and a finite expectation $1/\mu _i$ as assumed in Assumption 1, Theorem 2 in Section XI.3 of Feller (1971) Page 367 shows that for any $\varepsilon >0$ there exists a $T_1>0$ such that

$$\begin{aligned} |M_{G_i}'(t)-\mu _i|\le \varepsilon \quad \text {for all }s>T_1. \end{aligned}$$

(116)

With the help of the above analysis, next we consider $\bar{A}_i(\cdot )$, the process describing how fluid of class i enters service. It follows from (57) that

$$\begin{aligned}&\limsup _{t\rightarrow \infty }\left| \frac{1}{t}\bar{A}_i(t) -\mu _i\frac{1}{t}\int _0^t\bar{Z}_i(s)ds \right| \\&\quad =\limsup _{t\rightarrow \infty } \left| \frac{1}{t}(\bar{Z}_i(t)-\bar{\mathscr {Z}}_i(0)(C_t))+ \frac{1}{t}\int _0^t\bar{Z}_i(t-s)dM_{G_i}(s) \right. \\&\qquad \left. -\frac{1}{t}\int _0^t\bar{\mathscr {Z}}_i(0)(C_{t-s})dM_{{G_i}}(s) -\mu _i\frac{1}{t}\int _0^t\bar{Z}_i(s)ds \right| \\&\quad {\mathop {=}\limits ^{(a)}}\limsup _{t\rightarrow \infty } \left| \frac{1}{t}\int _0^t M'_{{G_i}}(t-s)\bar{Z}_i(s)ds -\mu _i\frac{1}{t}\int _0^t\bar{Z}_i(s)ds \right| \\&\quad {\mathop {\le }\limits ^{(b)}}\limsup _{t\rightarrow \infty } \left[ \frac{1}{t}{\int _0^{t-T_1}|M'_{G_i}(t-s)\!-\!\mu _i|ds}\! +\!\frac{1}{t} {\int _{t-T_1}^{t}M'_{G_i}(t-s)ds \!+\!\frac{1}{t}\int _{t-T_1}^t\mu _ids} \right] \\&\quad {\mathop {\le }\limits ^{(c)}} \varepsilon , \end{aligned}$$

where (a) is due to (15) and (115); (b) is due to (15); (c) is due to (116). Since $\varepsilon$ can be arbitrarily small, we obtain (111).

It follows from (17) that $\bar{R}_i(t)\le \lambda _i t+\bar{R}_i(0)$. Then by (53) we have $\lim \limits _{t\rightarrow \infty } \frac{1}{t}\bar{Q}_i(t)=0$. Thus, as a consequence of (111), the limits (112) and (113) immediately hold by Eqs. (21) and (22). $\square$

Tightness of the fluid-scaled processes

1.1 Tightness under any control policy

The main result here is the tightness proved in Lemmas B.4 and B.5. We will present their proofs after proving the following auxiliary lemma.

Lemma B.3

Given Assumptions 1 and 2, for each $\varepsilon ,\eta >0$ and $T>0$ there exists an $n_0$ such that when $n>n_0$,

$$\begin{aligned} \mathbb {P}^n\{\max _{i\in \mathscr {I}}\sup _{t\in [0,T]} \Big \vert \bar{Q}^n_i(t)- \lambda _i\int _0^{\omega _i^n(t)}F_i^c(s)ds\Big \vert \le \varepsilon \}\ge 1-\eta , \end{aligned}$$

(117)

where ${\omega }^n_i(t)$ is the waiting time of the earliest arrived class-i customer in the virtual buffer at time t.

Proof

It immediately follows from Assumption 2 that for each $\varepsilon ,\eta >0$ there exists an $n_0$ such that for all $n>n_0$,

$$\begin{aligned} \mathbb {P}^n(\max _{i\in \mathscr {I}}\sup _{0\le s< t\le T} |\bar{E}^n_i(s,t)-\lambda _i(t-s)|\le \frac{\varepsilon }{2}) \ge 1-\eta . \end{aligned}$$

(118)

Denote the event in (118) by $\varOmega _{E}^n$.

Let $\{t_k\}_{k=0}^K$ be a partition of the interval $[\tau ,t]$ such that $\tau =t_0<t_1<\cdots <t_K=t$ and $\max _{k}(t_{k+1}-t_k)<\delta$ for some $\delta >0$. We can break the sum into K parts,

$$\begin{aligned} \frac{1}{n} \sum _{l={E}^n_i(\tau )+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}(C_{t-{{a}}^n_{i,l}}) =\sum _{k=0}^{K-1}\frac{1}{n} \sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})} \delta _{{{u}}^n_{i,l}}(C_{t-{{a}}^n_{i,l}}). \end{aligned}$$

Note that $a_{i,l}\in [t_k,t_{k+1}]$ for all $l\in [{E}^n_i(t_k)+1,{E}^n_i(t_{k+1})]$. So on the event $\varOmega _E^n$ we can apply the Glivenko-Cantelli theorem (cf. Theorem 2.47 in Durrett (2010), Lemma B.1 in Zhang (2013)) to obtain

$$\begin{aligned}&\frac{1}{n}\sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})} \delta _{{{u}}^n_{i,l}}(C_{t-{{a}}^n_{i,l}})\\&\le \frac{1}{n}\sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})} \delta _{{{u}}^n_{i,l}}(C_{t-t_{k+1}})\\&\le \bar{E}^n_i(t_k,t_{k+1}){\nu }_{F_i}(C_{t-t_{k+1}})+\varepsilon \\&\quad \quad \le \bar{E}_i(t_k,t_{k+1}) \nu _{F_i}(C_{t-t_{k+1}})+2\varepsilon = \lambda _i\int _{t_k}^{t_{k+1}} F_i^c(t-t_{k+1})ds+2\varepsilon \end{aligned}$$

for all large n, where $\nu _{F_i}$ is the probability measure of the patience time distribution $F_i$. Similarly, we can obtain the corresponding inequality of the opposite direction

$$\begin{aligned} \frac{1}{n}\sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})} \delta _{{{u}}^n_{i,l}}(C_{t-{{a}}^n_{i,l}}) \ge \lambda _i\int _{t_k}^{t_{k+1}} F_i^c(t-t_k)ds-2\varepsilon . \end{aligned}$$

Note that $\sum _{k=0}^{K-1}\lambda _i\int _{t_k}^{t_{k+1}}F_i^c(t-t_{k+1})ds$ and $\sum _{k=0}^{K-1}\lambda _i\int _{t_k}^{t_{k+1}}F_i^c(t-t_{k})ds$ serve as the upper and lower Reimann sums of the integral $\lambda _i\int _{\tau }^t F_i^c(t-s)ds$. We can make $\varepsilon$ arbitrarily small by making the partition finer. Thus, we can conclude that for any $\varepsilon _0$ there exists an $n_0$ such that for all $n> n_0$ there is

$$\begin{aligned} \Big \vert \frac{1}{n} \sum _{l={E}^n_i(\tau )+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}(C_{t-{{a}}^n_{i,l}}) -\lambda _i\int _{\tau }^tF_i^c(t-s)ds\Big \vert <\varepsilon _0. \end{aligned}$$

(119)

According to the definition of the virtual buffer we have $\bar{R}^n_i(t)=\bar{E}^n_i(t)-\bar{E}^n_i(t-\omega _i^n(t))$. From (10), this implies

$$\begin{aligned} \bar{B}^n_i(t) =\bar{E}^n_i(t-{\omega }^n_i(t)). \end{aligned}$$

(120)

Plugging $\tau =t-\omega _i^n(t)$ into (119), and by (11) and (120) the result (117) holds. $\square$

Lemma B.4

Given Assumptions 1 and 2, for any control policy $\pi ^n\in \varPi ^n$ the sequences of fluid-scaled stochastic processes $\{\bar{A}^n_i\}$, $\{\bar{L}^n_i\}$, $\{\bar{S}^n_i\}$, $\{\bar{B}^n_i\}$, $\{\bar{X}^n_i\}$, $\{\bar{Q}^n_i\}$, $\{\bar{Z}^n_i\}$ and $\{\bar{R}^n_i\}$ for all $i\in \mathscr {I}$ are tight.

Proof

By the convergence of the initial condition (25), for any $\eta >0$, there exists a compact set ${\mathbf {K}}_0\subset {\mathbf {M}}$ such that

$$\begin{aligned} \liminf _{n\rightarrow \infty } \mathbb {P}^n\{\bar{\mathscr {R}}^n_i(0)\in {\mathbf {K}}_0 \text { and } \bar{\mathscr {Z}}^n_i(0)\in {\mathbf {K}}_0 \text { for all } i\in \mathscr {I}\} \ge 1-\eta . \end{aligned}$$

(121)

Denote the event in the above probability by $\varOmega _0^n$. On this event, by (9) and the definition of compact set in the space ${\mathbf {M}}$ (see Theorem 15.7.5 in Kallenberg (1986)), there exists an $M_0>0$ such that

$$\begin{aligned} \bar{R}^n_i(0)\le M_0, \ \ \bar{Q}^n_i(0)\le M_0 \ \text {\ and \ } \bar{Z}^n_i(0)\le M_0. \end{aligned}$$

Clearly, on the event $\varOmega _0^n$, we have $\bar{X}^n_i(0)\le 2M_0$ and $|\bar{B}^n_i(0)|=\bar{R}^n_i(0)\le M_0$ following from (3) and (10). Additionally, we have $\bar{A}^n_i(0)=\bar{L}^n_i(0)=\bar{S}^n_i(0)=0$. Thus, condition (i) in Theorem 15.5 of Billingsley (1968) is satisfied by all the sequences of stochastic processes.

Now we turn to analyze the oscillation boundedness. We start by considering the oscillation bound of the sequence of service completion processes $\{\bar{S}_i^{n}\}$. In view of (5), (12) and (13), $\bar{S}_i^{n}$ can be recovered as

$$\begin{aligned} \bar{S}^n_i(t)&=\frac{1}{n} \sum _{l=-{R}^n_i(0)-{Z}^n_i(0)+1}^{-{R}^n_i(0)} \delta _{{{v}}^n_{i,l}}((0,t]) +\frac{1}{n}\sum _{l=-{R}^n_i(0)+1}^{{B}^n_i(t)} \delta _{(u_{i,l}^n,v_{i,l}^n)}(C_{\tau _{i,l}^n-a_{i,l}^n})\\&\quad \times ((0,t-\tau _{i,l}^n]). \end{aligned}$$

It can then be seen from the above and (12) that for any $0\le s\le t$,

$$\begin{aligned} \bar{S}^n_i(s,t) =\bar{\mathscr {Z}}^n_i(s)((0,t-s]) +\frac{1}{n}\sum _{l={B}^n_i(s)+1}^{{B}^n_i(t)} \delta _{(u_{i,l}^n,v_{i,l}^n)}(C_{\tau _{i,l}^n-a_{i,l}^n}) \times ((0,t-\tau _{i,l}^n]). \end{aligned}$$

In the above equation $l={B}^n_i(s)+1,\ldots ,{B}^n_i(t)$, which implies the start service times ${{\tau }}^n_{i,l}\in [s,t]$. Combining this with (10), for any $t\in [0,T]$ we have

$$\begin{aligned} \bar{S}^n_i(s,t) \le \bar{\mathscr {Z}}^n_i(s)((0,t-s]) +\frac{1}{n}\sum _{l=-{R}^n_i(0)+1}^{{E}^n_i(T)} \delta _{v_{i,l}^n}((0,t-s]). \end{aligned}$$

(122)

Following the same argument in Lemma 5.3 of Zhang (2013), we can see that under Assumptions 1 and 2, for each $\varepsilon ,\eta >0$ and $T>0$ there exists a $\kappa >0$ (depending on $\varepsilon$ and $\eta$) such that

$$\begin{aligned} \liminf _{n\rightarrow \infty } \mathbb {P}^n(\max _{i\in \mathscr {I}} \sup _{t\in [0,T]}\sup _{x\in \mathbb {R}_+} \bar{\mathscr {Z}}^n_i(t)([x,x+\kappa ]) \le \varepsilon ) \ge 1-\eta . \end{aligned}$$

(123)

Denote the event in (123) by $\varOmega _{\text {Reg}}^n(\kappa )$. The first term on the right side of (122) is always bounded by $\varepsilon$ on $\varOmega _{\text {Reg}}^n(\kappa )$ as long as $t-s<\kappa$. Denote the event in (117) by $\varOmega _{Q}^n$ and let

$$\begin{aligned} \varOmega ^n =\varOmega _{0}^n \cap \varOmega _E^n \cap \varOmega _{\text {Reg}}^n(\kappa ) \cap \varOmega _{Q}^n. \end{aligned}$$

From (123), (118), (117) and (121)

$$\begin{aligned} \liminf _{n\rightarrow \infty } \mathbb {P}^n\{\varOmega ^n\}\ge 1-\eta . \end{aligned}$$

In the remainder of the proof, all random objects are evaluated on a fixed sample path in $\varOmega ^n$. On this event we have

$$\begin{aligned} \quad \frac{1}{n}\sum _{l=-{R}^n_i(0)+1}^{{E}^n_i(T)} \delta _{v_{i,l}^n}((0,t-s])&\le (\bar{E}^n_i(T)+\bar{R}^n_i(0)) \nu _{G_i}((0,t-s])+ \frac{\varepsilon }{2}\nonumber \\&\le (M_0+2\lambda _i T) \nu _{G_i}((0,t-s])+ \frac{\varepsilon }{2}, \end{aligned}$$

(124)

where the first inequality follows from the Glivenko-Cantelli theorem with $\nu _{G_i}$ being the probability measure of the service time distribution $G_i$. Since ${G_i}$ is absolutely continuous, we can choose $t-s$ small enough such that $\nu _{G_i}((0,t-s]) \le \frac{\varepsilon }{2(M_0+2\lambda _i T)}$. Then by (122) and (124), we have for all large n,

$$\begin{aligned} \bar{S}^n_i(s,t)\le 2\varepsilon . \end{aligned}$$

(125)

By the definition of $\varOmega _{E}^n$, when $t-s\le \frac{\varepsilon }{2\lambda }$ we have for all large n,

$$\begin{aligned} \bar{E}^n_i(s,t)\le \varepsilon . \end{aligned}$$

(126)

Combing the above two inequalities with (23) yields,

$$\begin{aligned} \bar{A}^n_i(s,t)\le 3I\varepsilon , \end{aligned}$$

(127)

as long as $t-s$ is small enough.

If the lth class-i customer abandons the queue in time interval [s, t], the sum of his patience time ${{u}}^n_{i,l}$ and arrival time ${{a}}^n_{i,l}$ should be in the interval [s, t], i.e., ${{u}}^n_{i,l}+{{a}}^n_{i,l}\in [s,t]$. Therefore,

$$\begin{aligned} \bar{L}^n_i(s,t) \le \frac{1}{n} \sum _{l=-{R}^n_i(0)+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}([s,t]-{{a}}^n_{i,l}). \end{aligned}$$

(128)

Let $\tau =t_0<t_1<\cdots <t_K=t$ be a partition of the interval $[\tau ,t]$. Then

$$\begin{aligned} \frac{1}{n} \sum _{l={E}^n_i(\tau )+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}([s,t]-{{a}}^n_{i,l})&= \sum _{k=0}^{K-1}\frac{1}{n} \sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})} \delta _{{{u}}^n_{i,l}}([s,t]-{{a}}^n_{i,l})\nonumber \\&\le \sum _{k=0}^{K-1}\frac{1}{n} \sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})} \delta _{{{u}}^n_{i,l}}([s-t_{k+1},t-t_k]), \end{aligned}$$

(129)

where the last inequality arises because on each sub-interval $[t_k,t_{k+1}]$ those l’s to be summed must satisfy $t_k\le {{a}}^n_{i,l}\le t_{k+1}$. It follows from the Glivenko-Cantelli theorem that

$$\begin{aligned} \frac{1}{n} \sum _{l={E}^n_i(t_k)+1}^{{E}^n_i(t_{k+1})}\!\! \delta _{{{u}}^n_{i,l}}([s-t_{k+1},t-t_k])\! \le \! (\bar{E}^n_i(t_{k\!+\!1})-\bar{E}^n_i(t_k)) {\nu }_{F_i}([s-t_{k+1},t\!-\!t_{k}]) \!+\!\frac{\varepsilon }{2K}. \end{aligned}$$

(130)

Since $F_i$ is absolutely continuous, we can make $t-s$ small enough and the partition fine enough such that

$$\begin{aligned} \nu _{F_i}([s-t_{k+1},t-t_{k}]) \le \frac{\varepsilon }{2(M_{0}+2\lambda T)}. \end{aligned}$$

(131)

It then follows from (129)–(131) that

$$\begin{aligned} \frac{1}{n} \sum _{l={E}^n_i(\tau )+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}([s,t]-{{a}}^n_{i,l}) \le \frac{\varepsilon }{2(M_0+2\lambda T)} [\bar{E}^n_i(t)-\bar{E}^n_i(\tau )]+\frac{\varepsilon }{2}. \end{aligned}$$

(132)

Recall that $\omega _i^n(t)$ denoted in Lemma B.3 is the waiting time of the earliest arrived class-i customer in the virtual buffer at time t. Therefore ${{a}}^n_{i,-{{R}}^n(0)+1}$, the arrival time of the earliest arrived class-i customer in the virtual buffer at the initial time point, equals to $0-\omega _i^n(0)$. So (17) and (120) yield ${B}^n_i(0)=-{R}^n_i(0)={E}^n_i({{a}}^n_{i,-{{R}}^n(0)+1})$. Plugging $\tau ={{a}}^n_{i,-{{R}}^n(0)+1}$ into (132) and combining (128), we obtain

$$\begin{aligned} \bar{L}^n_i(s,t)&\le \frac{\varepsilon }{2(M_0+2\lambda T)} [\bar{E}^n_i(t)+\bar{R}^n_i(0)]+\frac{\varepsilon }{2} \le \varepsilon \end{aligned}$$

(133)

for all large n. Thus the oscillation bound of $\bar{L}^n_i(\cdot )$ is proved.

By balance equation (4)

$$\begin{aligned} |\bar{Q}^n_i(t)-\bar{Q}^n_i(s)| \le \bar{E}^n_i(s,t)+\bar{A}^n_i(s,t)+\bar{L}^n_i(s,t)\le 3(I+1)\varepsilon \end{aligned}$$

(134)

for all large n and small enough $t-s$, where the last inequality is due to (126), (127) and (133). In view of (120), to prove the oscillation bound of $\bar{B}^n_i(\cdot )$ an essential step is to prove that of ${\omega }^n_i(\cdot )$. By Lemma B.3 and (134), when $t-s$ is small enough we have

$$\begin{aligned}&|\int _0^{{\omega }^n_i(t)}F_i^c(x)dx-\int _0^{{\omega }^n_i(s)}F_i^c(x)dx| \le |\frac{\bar{Q}^n_i(t)}{\lambda _i}-\frac{\bar{Q}^n_i(s)}{\lambda _i}| +2\frac{\varepsilon }{\lambda _i} \le 3(I+2)\frac{\varepsilon }{\lambda _i} \end{aligned}$$

(135)

for all large n. Denote $S_{F_i}=\inf \{x\ge 0: F(x)=1\}$. Observe that $F_{i,d}^{-1}(\cdot )$ is continuous on $[0,\infty )$ and $\omega _i^n(\cdot )<S_{F_i}$ since we can remove any customer whose waiting time exceeds $S_{F_i}$ from the virtual buffer (without affecting the dynamics). So for any $\varepsilon _2>0$,

$$\begin{aligned}&\quad |{\omega }^n_i(t)-{\omega }^n_i(s)| =|F_{i,d}^{-1}\left( \int _0^{{\omega }^n_i(t)}F_i^c(x)dx \right) -F_{i,d}^{-1}\left( \int _0^{{\omega }^n_i(s)}F_i^c(x)dx\right) | \le \varepsilon _2 \end{aligned}$$

as long as $\varepsilon$ in (135) is small enough. By (120) and the definition of $\varOmega ^n_E$, the oscillation of $\bar{B}^n_i(\cdot )$ becomes

$$\begin{aligned} |\bar{B}^n_i(s,t)|&=|\bar{E}^n_i(t-\omega _i^n(t))-\bar{E}^n_i(s-\omega _i^n(s))|\\&\le \lambda |t-s-({\omega }^n_i(t)-{\omega }^n_i(s))|+\varepsilon \\&\le \lambda |t-s|+\lambda \varepsilon _2+\varepsilon , \end{aligned}$$

which can be made smaller than a multiple of $\varepsilon$ by choosing $|t-s|$ and $\varepsilon _2$ small enough. Thus the oscillation bound of $\bar{B}^n_i(\cdot )$ is proved.

So we can conclude that the cumulative processes $\bar{A}^n_i$, $\bar{L}^n_i$, $\bar{S}^n_i$ and $\bar{B}^n_i$ all satisfy condition (ii) in Theorem 15.5 of Billingsley (1968). Thus, we have the desired tightness. The tightness of the head-count processes $\bar{X}^n_i$, $\bar{Q}^n_i$, $\bar{Z}^n_i$ and $\bar{R}^n_i$ directly follows from (4), (5) and (10). $\square$

With the help of the tightness of the head-count processes, we now prove the following lemma.

Lemma B.5

Given Assumptions 1 and 2, for any control policy $\pi ^n\in \varPi ^n$ the sequence of fluid-scaled measure-valued stochastic processes $\{(\bar{\mathscr {R}}^n_i,\bar{\mathscr {Z}}^n_i), n\in \mathbb {N}\}$, $i\in \mathscr {I}$, are tight.

Proof

When $t-s\le \frac{\varepsilon }{2\lambda _i}$, by the definition of $\varOmega _{E}^n$ we have $\bar{E}^n_i(s,t)\le \varepsilon$. For any $s<t$ and any Borel set $C\subset \mathbb {R}$, consider the following two cases:

If ${E}^n_i(s)> {B}^n_i(t)$, then by (11),

$$\begin{aligned}&\quad \bar{\mathscr {R}}^n_i(t)(C)-\bar{\mathscr {R}}^n_i(s)(C^\varepsilon )\\&=-\frac{1}{n}\sum _{l={B}^n_i(s)+1}^{{B}^n_i(t)} \delta _{{{u}}^n_{i,l}}(C^\varepsilon +s-{{a}}^n_{i,l}) +\frac{1}{n}\sum _{l={E}^n_i(s)+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}(C+t-{{a}}^n_{i,l})\\&\quad +\frac{1}{n}\sum _{l={B}^n_i(t)+1}^{{E}^n_i(s)} \left[ \delta _{{{u}}^n_{i,l}}(C+t-{{a}}^n_{i,l}) -\delta _{{{u}}^n_{i,l}}(C^\varepsilon +s-{{a}}^n_{i,l}) \right] \\&\le \bar{E}^n_i(s,t). \end{aligned}$$

The first term on the right-hand side of the above equation is clearly non-positive since ${B}^n_i(t)$ is non-decreasing. Note that when $t-s\le \varepsilon$, $C+t-{{a}}^n_{i,l}\subseteq C^\varepsilon +s-{{a}}^n_{i,l}$ for all $l\in \mathbb {Z}$, which implies that the third term in the above equation is less than zero. Therefore the inequality follows.

If ${E}^n_i(s)\le {B}^n_i(t)$, then by the definition of $\bar{\mathscr {R}}^n_i(C)$ in (11) that

$$\begin{aligned} \bar{\mathscr {R}}^n_i(t)(C)-\bar{\mathscr {R}}^n_i(s)(C^\varepsilon ) \le \bar{\mathscr {R}}^n_i(t)(C)\le \frac{1}{n} \sum _{l={E}^n_i(s)+1}^{{E}^n_i(t)} \delta _{{{u}}^n_{i,l}}(C+t-{{a}}^n_{i,l}) \le \bar{E}^n_i(s,t). \end{aligned}$$

Therefore, for any case there will always be

$$\begin{aligned} \bar{\mathscr {R}}^n_i(t)(C)-\bar{\mathscr {R}}^n_i(s)(C^\varepsilon ) \le \bar{E}^n_i(s,t) \le \varepsilon , \end{aligned}$$

(136)

as long as $t-s$ is small enough.

On the other hand, when t and s are close enough combining (10) and (136) gives

$$\begin{aligned} \bar{\mathscr {R}}^n_i(s)(\mathbb {R}\setminus C^\varepsilon ) -\bar{\mathscr {R}}^n_i(t)(\mathbb {R}\setminus C) \le \bar{B}^n_i(s,t)\le \varepsilon , \end{aligned}$$

(137)

where the last inequality is owing to the oscillation bound of $\bar{B}^n_i$ shown in the proof of Lemma B.4. It follows from the fact $\mathbb {R}\setminus C\subseteq \{\mathbb {R}\setminus C^\varepsilon \}^{2\varepsilon }$ and C could be any Borel set in $\mathbb {R}$ that the above inequality yields

$$\begin{aligned} \bar{\mathscr {R}}^n_i(s)(C)-\bar{\mathscr {R}}^n_i(t)(C^{2\varepsilon }) \le 2\varepsilon . \end{aligned}$$

(138)

Combining (136) and (138), we have

$$\begin{aligned} \mathbf {d}[\bar{\mathscr {R}}^n_i(t),\bar{\mathscr {R}}^n_i(s)] \le \varepsilon , \end{aligned}$$

(139)

where $\mathbf {d}$ is the Prohorov metric defined in (1).

Give a new index $l={A}^n_i(s)+1,\ldots ,{A}^n_i(t)$ to class-i customers who enter service in time interval (s, t] according to the time ${{\tau }}^n_{i,l}$ at which they start service. It follows from (12) and (13) that

$$\begin{aligned} \bar{\mathscr {Z}}^n_i(t)(C) =\bar{\mathscr {Z}}^n_i(s)(C+t-s) +\frac{1}{n}\sum _{l={A}^n_i(s)+1}^{{A}^n_i(t)} \delta _{{{v}}^n_{i,l}}(C+t-{{\tau }}^n_{i,l}). \end{aligned}$$

Then

$$\begin{aligned} \bar{\mathscr {Z}}^n_i(t)(C)-\bar{\mathscr {Z}}^n_i(s)(C+t-s) \le \bar{A}^n_i(s,t)\le \varepsilon , \end{aligned}$$

as long as $t-s$ is small enough, where the last inequality holds due to the oscillation bound of $\bar{A}^n_i$ shown in the proof of Lemma B.4. Note that when $t-s\le \varepsilon , C+t-s\subseteq C^\varepsilon$. Thus, we have

$$\begin{aligned} \bar{\mathscr {Z}}^n_i(t)(C)-\bar{\mathscr {Z}}^n_i(s)(C^\varepsilon ) \le \bar{A}^n_i(s,t)\le \varepsilon . \end{aligned}$$

(140)

Similar to (137), by (5) and the above we have

$$\begin{aligned} \bar{\mathscr {Z}}^n_i(s)(\mathbb {R}_+ \setminus C^\varepsilon ) -\bar{\mathscr {Z}}^n_i(t)(\mathbb {R}_+ \setminus C)\le \bar{S}^n_i(s,t)\le \varepsilon , \end{aligned}$$

for t and s close enough. Since the above inequality holds for any Borel set $C\subset \mathbb {R}_+$, we can use the same argument as that for (138) to obtain

$$\begin{aligned} \bar{\mathscr {Z}}^n_i(s)(C)-\bar{\mathscr {Z}}^n_i(t)(C^{2\varepsilon }) \le 2\varepsilon . \end{aligned}$$

(141)

So (140) and (141) imply that

$$\begin{aligned} \mathbf {d}[\bar{\mathscr {Z}}^n_i(t),\bar{\mathscr {Z}}^n_i(s)]\le \varepsilon . \end{aligned}$$

(142)

The oscillation bound condition in Theorem 3.7.2 of Ethier and Kurtz (1986) follows from (139) and (142). The compact containment property can be verified using the same argument in Lemma 5.1 of Zhang (2013). Thus $\bar{\mathscr {R}}^n_i$ and $\bar{\mathscr {Z}}^n_i$ are tight. $\square$

1.2 Tightness under virtual allocation policies

Lemma B.6

Given Assumptions 1, 2 and 4, for any sequence of virtual allocation policies $\{\pi ^n(z^n)\}$, the sequences of fluid-scaled stochastic processes $\{\bar{A}^n_{ij}(\cdot )\}$, $\{\bar{Z}^n_{ij}(\cdot )\}$ and $\{\bar{S}^n_{ij}(\cdot )\}$, $i,j\in \mathscr {I}$, are tight.

Proof

As we can see, condition (i) in Theorem 15.5 of Billingsley (1968) holds due to the fact that $\bar{A}^n_{ij}(0)=\bar{S}^n_{ij}(0)=0$. Each class-i customer having completed service from service group j must be counted as one instance of service completions of class-i customers in the whole server pool. Therefore we have $\bar{S}^n_{ij}(s,t)\le \bar{S}^n_i(s,t)$. Similarly, $\bar{A}^n_{ij}(s,t)\le \bar{A}^n_i(s,t)$. Note that $\bar{S}^n_{ij}(\cdot )$ and $\bar{A}^n_{ij}(\cdot )$ are also nondecreasing. Thus the oscillation bounds of $\bar{S}^n_{ij}$ and $\bar{A}^n_{ij}$ are implied by those of $\bar{S}^n_{i}$ and $\bar{A}^n_{i}$, which have been proven in Lemma B.4. So $\bar{S}^n_{ij}$ and $\bar{A}^n_{ij}$ are tight. Due to the balance equation in (42), the tightness of $\{\bar{Z}^n_{ij}(t)\}$ immediately follows. $\square$