The residual time approach for (Q, r) model under perishability, general lead times, and lost sales

Abstract

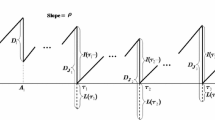
We consider a (Q, r) perishable inventory system with state-dependent compound Poisson demands with a random batch size, general lead times, exponential shelf times, and lost sales. We assume $r<Q$ and analyze the system using an embedded Markov process at the replenishment points. Using the queueing and Markov chain decomposition approach, we characterize the distribution of the residual lead time and derive the stationary distribution of the inventory level. We construct closed-form expressions for the expected total long-run average cost function. The closed form allows us to efficiently obtain, numerically, the optimal Q and r parameters. Numerical study provides several guidelines for the optimal control. For example, we show that approximating the lead time distribution by an exponential one only works when the optimal reorder point of the approximation is very small; in other cases the usage of the exact distribution can lead to substantial cost savings (up to 14%). We further provide intuition insight on the optimal controls and how they depend on different factors, e.g., the lead time variability, and the demand features (arrival rate, size and variability).

Appendices

Appendix A: Phase-type distribution

A phase-type distributed random variable X with representation $PH(\varvec{\beta ,}\mathbb {S})$ of order n is the distribution of the time until absorption into state $n+1$ of a continuous-time Markov chain $\mathcal {J}(t)$ with an infinitesimal generator $Q=\left( \begin{array} [c]{cc} \mathbb {S}\, &{} \mathbf{S} ^{o}\\ \mathbf{0} \, &{} {\small 0} \end{array} \right)$, where $\mathbb {S}$ is the transition rate matrix, $\mathbf{S} ^{o}$ describes the absorption rate vector into state $n+1,$ and $\varvec{\beta }$ is the initial probability vector on the set of transient states. For more details on the phase-type distribution, see Neuts (1981).

Let X and Y be two independent random variables; assume that X is $PH(\varvec{\tau },\mathbb {T})$ with n phases, and that Y is $PH(\varvec{\beta },\mathbb {S})$ with m phases. Theorem 2.6.4 of Latouche and Ramaswami (1999) yields that the random variable $Z=\min (X,Y)$ has a PH distribution with representation $PH(\varvec{\gamma },\mathbb {C})$ with nm phases, where

$$\begin{aligned} \varvec{\gamma }=\varvec{\tau }\otimes \varvec{\beta },\, \mathbb {C} =\mathbb {T}\oplus \mathbb {S}. \end{aligned}$$

(Note that $\otimes$ is the Kronecker product, and $\oplus$ is the Kronecker sum; i.e., $\varvec{\gamma }=(\tau _{1}\varvec{\beta }\ldots \tau _{n}\beta )$ and $\mathbb {C}=\mathbb {T}\otimes \mathbb {I}+\mathbb {I}\otimes \mathbb {S}$).

Appendix B: Proof of Lemma 2

We note that Eq. (21) follows from the discussion above the lemma. Next, for $0<n\le r,$

$$\begin{aligned} R_{n}^{*}(\theta )&=E[e^{-\theta (R_{n+1}-T_{\lambda _{_{n}}})}\mid T_{\lambda _{n}}<\min (T_{\mu },R_{n+1})]\nonumber \\&\quad =P(R_{n+1}-T_{\lambda _{n}}\le T_{\theta }\mid T_{\lambda _{n}}<\min (T_{\mu },R_{n+1}))\nonumber \\&\quad =\frac{P(R_{n+1}-T_{\lambda _{n}}\le T_{\theta },T_{\lambda _{n}}<\min (R_{n+1},T_{\mu }))}{P(T_{\lambda _{n}}<\min (R_{n+1},T_{\mu }))} . \end{aligned}$$

(52)

As for the denominator,

$$\begin{aligned}&P(R_{n+1}-T_{\lambda _{n}}\le T_{\theta },T_{\lambda _{n}}<T_{\mu } ,T_{\lambda _{n}}<R_{n+1})\nonumber \\&\quad = {\displaystyle \int \limits _{x=0}^{\infty }} {\displaystyle \int \limits _{t=0}^{x}} e^{-\theta (x-t)}e^{-\mu t}\lambda _{n}e^{-\lambda _{n}t}f_{R_{n+1} }(x)dtdx\nonumber \\&\quad =\frac{\lambda _{n}}{\lambda _{n}+\mu -\theta }\left[ R_{n+1}^{*} (\theta )-R_{n+1}^{*}(\lambda _{n}+\mu )\right] , \end{aligned}$$

(53)

where $f_{R_{n}}(x),n=1,\ldots ,r$ is the PDF of the observed residual lead time, $R_{n}.$ Applying (10) leads to the numerator

$$\begin{aligned} P(T_{\lambda _{n}}\le \min (R_{n+1},T_{\mu }))=\frac{\lambda _{n}}{\lambda _{n} +\mu }[1-R_{n+1}^{*}(\lambda _{n}+\mu )]. \end{aligned}$$

(54)

Summarizing (52)–(54) yields (22) . Note that when $\theta =\lambda _{n}$ or $\theta =\lambda _{n}+\mu$, one can use L’Hopital’s rule to extend the results.