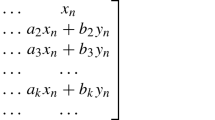Abstract
We study the facet defining inequalities of the convex hull of a mixed-integer bilinear covering arising in trim-loss (or cutting stock) problem under the framework of disjunctive cuts. We show that all of them can be derived using a disjunctive procedure. Some of these are split cuts of rank one for a convex mixed-integer relaxation of the covering set, while others have rank at least two. For certain linear objective functions, the rank-one split cuts are shown to be sufficient for finding the optimal value over the convex hull of the covering set. A relaxation of the trim-loss problem has this property, and our computational results show that these rank-one inequalities find the lower bound quickly.



Similar content being viewed by others
References
Andersen K, Jensen AN (2013) Intersection cuts for mixed integer conic quadratic sets. In: Goemans M, Correa J (eds) Integer programming and combinatorial optimization. Springer, Berlin, pp 37–48
Atamtürk A, Narayanan V (2010) Conic mixed-integer rounding cuts. Math Program A 122:1–20
Balas E (1979) Disjunctive programming. Ann Discrete Math 5:3–51
Balas E (1998) Disjunctive programming: properties of the convex hull of feasible points. Discrete Appl Math 58(1–3):3–44
Balas E, Ceria S, Cornuéjols G (1993) A lift-and-project cutting plane algorithm for mixed 0–1 programs. Math Program 58:295–324
Belloti P (2012) Disjunctive cuts for nonconvex MINLP. In: Lee J, Leyffer S (eds) Mixed integer nonlinear programming. The IMA volumes in mathematics and its applications, vol 154. Springer, Berlin, pp 117–144
Bonami P (2011) Lift-and-project cuts for mixed integer convex programs. In: Günlük O, Woeginger JG (eds) Integer programming and combinatoral optimization. Springer, Berlin, pp 52–64
Caparara A, Letchford AN (2003) On the separation of split cuts and related inequalities. Math Program 94:279–294
Çezik MT, Iyengar G (2005) Cuts for mixed 0–1 conic programming. Math Program A 104:179–202
Conforti M, Cornuéjols G, Zambelli G (2010) Polyhedral approaches to mixed integer linear programming. In: Jünger M, Liebling ThM, Naddef D, Nemhauser GL, Pulleyblank WR, Reinelt G, Rinaldi , Wolsey LA (eds) 50 Years of integer programming. Springer, Berlin, pp 1958–2008
Cook W, Kannan R, Schrijver A (1990) Chvátal closures for mixed integer programming problems. Math Program 47:155–174
Cornuéjols G (2008) Valid inequalities for mixed integer linear programs. Math Program B 112:3–44
Cutting stock test instances and results. http://www.math.tu-dresden.de/~capad/cpd-ti.html. Last Accessed 7 Dec 2019
Dadush D, Dey SS, Vielma JP (2011) The split closure of a strictly convex body. Oper Res Lett 39:121–126
Dash S, Dobbs NB, Günlük O, Nowicki TJ, Swirszcz GM (2014) Lattice-free sets, multi-branch split disjunctions, and mixed-integer programming. Math Program A 145:483–508
Dey S (2011) A note on the split rank of intersection cuts. Math Program A 130:107–124
Dey S, Louveaux Q (2011) Split rank of triangle and quadrilateral inequalities. Math Oper Res 36(3):432–461
Dey SS, Santana A, Wang Y (2019) New SOCP relaxation and branching rule for bipartite bilinear programs. Optim Eng 20:307–336
Forrest J, Lougee-Heimerl R (2005) CBC (Coin-or Branch-and-Cut) Solver. https://projects.coin-or.org/Cbc. Accessed 20 Dec 2019
Forrest J, Saltzman M, Hafer L, Hall J (2004) COIN-OR Linear Program Solver (CLP). https://projects.coin-or.org/Clp. Accessed 20 Dec 2019
Garey MR, Johnson DS (1979) Computers and intractability: a guide to the theory of NP-completeness. W.H. Freeman and Co., New York
Gau T, Wascher G (1995) CUTGEN1: a problem generator for the standard one-dimensional cutting stock problem. Eur J Oper Res 84:572–579
Gomory RE (1960) Solving linear programming problems in integers. In: Bellman MHR (ed) Combinatorial analysis. Proceedings of symposia in applied mathematics, vol 10, pp 269–308
Gomory RE (1969) Some polyhedra related to combinatorial problems. Linear Algebra Appl 2:451–558
Harjunkoski I, Westerlund T, Porn R, Skrifvars H (1998) Different transformations for solving non-convex trim-loss problems by MINLP. Eur J Oper Res 105:594–603
Jeroslow RC (1973) There cannot be any algorithm for integer programming with quadratic constraints. Oper Res 21(1):221–224
Katta GM, Santosh NK (1987) Some NP-complete problems in quadratic and nonlinear programming. Math Program B 39:117–129
Kılınç MR, Linderoth JT, Luedtke J (2010) Effective separation of disjunctive cuts for convex mixed integer nonlinear programs. Technical Report, University of Wisconsin, Madison
Letchford AN (2010) Integer quadratic quasi-polyhedra. In: Eisenbrand F, Shepherd FB (eds) Integer programming and combinatorial optimization. Springer, Berlin, pp 258–270
Mitchell S, Kean A, Mason A, O’Sullivan M, Phillips A (2011) PuLP. https://www.coin-or.org/PuLP/
Modaresi S, Kılınç MR, Vielma JP (2015) Split cuts and extended formulations for mixed integer conic quadratic programming. Oper Res Lett 43:10–15
Modaresi S, Kılınç MR, Vielma JP (2016) Intersection cuts for nonlinear integer programming: convexification techniques for structured sets. Math Program A 155:575–611
Nemhauser GL, Wolsey LA (1988) Integer and combinatorial optimization. Wiley, New York
Nemhauser GL, Wolsey LA (1990) A recursive procedure to generate all cuts for 0–1 mixed-integer programs. Math Program B 46:379–390
Owen JH, Mehrotra S (2001) A disjunctive cutting plane procedure for general mixed integer linear programs. Math Program A 89:437–448
Rahman H, Mahajan A (2019) Facets of a mixed-integer bilinear covering set with bounds on variables. J Glob Optim 74:417–442
Saxena A, Bonami P, Lee J (2008) Disjunctive cuts for non-convex mixed integer quadratically constrained programs. In: Lodi A, Panconesi A, Rinaldi G (eds) Integer programming and combinatorial optimization. Springer, Berlin, pp 17–33
Stubs RA, Mehrotra S (1999) A branch-and-cut method for 0–1 mixed convex programming. Math Program A 86:515–532
Tawarmalani M, Richard JP, Chung K (2010) Strong valid inequalities for orthogonal disjunctions and bilinear covering sets. Math Program B 124:481–512
Umetani S, Yagiura M, Ibaraki T (2003) One dimensional cutting stock problem to minimize the number of different patterns. Eur J Oper Res 146:388–402
Vanderbeck F (2000) Exact algorithm for minimising the number of setups in the one-dimensional cutting stock problem. Oper Res 48(6):915–926
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Additional proofs
Appendix: Additional proofs
Proposition 10
Let \(j, k \in \mathbb {N}\) with \(j \ne k\), then the following two relations
cannot hold simultaneously for any non-negative integer \(\pi _0\).
Proof
Without loss of generality let \(k > j\). Note that, it is equivalent to prove that \(\sqrt{k(k - 1)} - \sqrt{j(j - 1)} \ge 1\). This is because, if \(\sqrt{k(k - 1)} - \sqrt{j(j - 1)} \ge 1\) holds, then both the values \(\sqrt{k(k - 1)}\) and \(\sqrt{j(j - 1)}\) cannot lie between two consecutive integers.
Also note that, since the function \(f(j) = \sqrt{j(j - 1)}\) is strictly increasing for \(j \in \mathbb {N}\), it is sufficient to prove the result when \(k = j + 1\), i.e., we show that \(\sqrt{j(j + 1)} - \sqrt{j(j - 1)} \ge 1\). Since we are dealing with positive numbers only, in our following steps of proof, we consider only the positive roots. For any \(j \in \mathbb {N}\),
This completes the proof. \(\square \)
Proposition 11
Let \(k \in \mathbb {N}\) with \(k \ge 2\). Consider the positive integers \(\mu _0, \mu \) with \(\mu \ge 1\). If \(\mu _0< \mu \sqrt{k(k - 1)} < \mu _0 + 1\) then \(k -1 < \frac{\mu _0 +1}{\mu } \le k\) and \(k -1 \le \frac{\mu _0}{\mu } < k\).
Proof
Since \(\mu _0< \mu \sqrt{k(k - 1)} < \mu _0 + 1\), then \(\frac{\mu _0 + 1}{\mu \sqrt{k(k - 1)}} > 1\). Again since \(\sqrt{\frac{k - 1}{k}} < 1\), we have
We show the other side of the desired inequality next. From the given condition we have,
Therefore, we have \(k -1 < \frac{\mu _0 +1}{\mu } \le k\).
Since \(\frac{\mu _0 +1}{\mu } \le k\), we have \(\frac{\mu _0}{\mu } < k\). It remains to show \(k - 1 \le \frac{\mu _0}{\mu }\). From the given relation we have
Therefore, we get \(k - 1 \le \frac{\mu _0}{\mu } < k\). \(\square \)
Rights and permissions
About this article
Cite this article
Rahman, H., Mahajan, A. On the facet defining inequalities of the mixed-integer bilinear covering set. Math Meth Oper Res 92, 545–575 (2020). https://doi.org/10.1007/s00186-020-00723-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-020-00723-9