Abstract
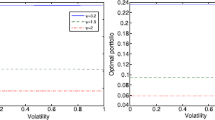
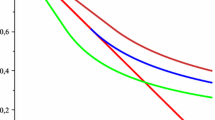
We study the standard utility maximization problem for a non-decreasing upper-semicontinuous utility function satisfying mild growth assumption. In contrast to the classical setting, we do not impose the assumption that the utility function is concave. By considering the concave envelope, or concavification, of the utility function, we identify the optimal solution for the optimization problem. We also construct the optimal solution for the constrained optimization problem, where the final endowment is bounded from above by a discrete random variable. We present several examples illustrating that our assumptions cannot be totally avoided.







Similar content being viewed by others
Availability of data and material
Not applicable
References
Aubin JP, Ekeland I (1984) Applied nonlinear analysis. Pure and Applied Mathematics (New York). John Wiley and Sons, Inc., New York. A Wiley-Interscience Publication
Aumann RJ, Perles M (1965) A variational problem arising in economics. J Math Anal Appl 11:488–503. https://doi.org/10.1016/0022-247X(65)90100-9
Carpenter JN (2000) Does option compensation increase managerial risk appetite? J Financ 55(5):2311–2331. https://doi.org/10.1111/0022-1082.00288
Dai M, Kou S, Qian S, Wan X (2019) Non-concave utility maximization without the concavification principle. Available at SSRN 3422276
Föllmer H, Schied A (2016) Stochastic finance. De Gruyter. https://doi.org/10.1515/9783110463453
Kahneman D, Tversky A (1979) Prospect theory: an analysis of decision under risk. Econometrica 47(2):263–291
Kramkov D, Schachermayer W (1999) The asymptotic elasticity of utility functions and optimal investment in incomplete markets. Ann Appl Probab 9(3):904–950. https://doi.org/10.1214/aoap/1029962818
Kramkov D, Schachermayer W (2003) Necessary and sufficient conditions in the problem of optimal investment in incomplete markets. Ann Appl Probab 13(4):1504–1516. https://doi.org/10.1214/aoap/1069786508
Merton RC (1969) Lifetime portfolio selection under uncertainty: the continuous-time case. Rev Econ Stat 51(3):247–257
Merton RC (1971) Optimum consumption and portfolio rules in a continuous-time model. J Econ Theory 3(4):373–413. https://doi.org/10.1016/0022-0531(71)90038-X
Reichlin C (2012) Non-concave utility maximization: optimal investment, stability and applications. Ph.D. thesis, ETH Zürich https://doi.org/10.3929/ethz-a-007615699.
Reichlin C (2013) Utility maximization with a given pricing measure when the utility is not necessarily concave. Math Financ Econ 7(4):531–556
Schied A (2005) Optimal investments for robust utility functionals in complete market models. Math Oper Res 30(3):750–764. https://doi.org/10.1287/moor.1040.0138
Schied A, Wu CT (2005) Duality theory for optimal investments under model uncertainty. Stat Decis 23(3):199–217. https://doi.org/10.1524/stnd.2005.23.3.199
Acknowledgements
O.B. thanks Prof. Dr. Mitja Stadje and Dr. Thai Nguyen for their help and support during her work on the topic. Authors thank Prof. Alexander Zimper and anonymous reviewers for careful reading and helpful suggestions.
Funding
The authors did not receive support from any organization for the submitted work.
Author information
Authors and Affiliations
Ethics declarations
Conflicts of interest/Competing interests
The authors declare that there are no competing interests.
Code availability
Not applicable
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Bahchedjioglou, O., Shevchenko, G. Optimal investments for the standard maximization problem with non-concave utility function in complete market model. Math Meth Oper Res 95, 163–181 (2022). https://doi.org/10.1007/s00186-022-00774-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-022-00774-0
Keywords
- Optimal investment
- Standard maximization problem
- Non-concave utility
- Non-convex optimization
- Constrained optimization