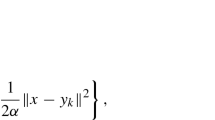Abstract
In this paper, we propose an inertial version of the Proximal Incremental Aggregated Gradient (abbreviated by iPIAG) method for minimizing the sum of smooth convex component functions and a possibly nonsmooth convex regularization function. First, we prove that iPIAG converges linearly under the gradient Lipschitz continuity and the strong convexity, along with an upper bound estimation of the inertial parameter. Then, by employing the recent Lyapunov-function-based method, we derive a weaker linear convergence guarantee, which replaces the strong convexity by the quadratic growth condition. At last, we present two numerical tests to illustrate that iPIAG outperforms the original PIAG.









Similar content being viewed by others
References
Aytekin A (2019) Asynchronous first-order algorithms for large-scale optimization: analysis and implementation. PhD thesis, KTH Royal Institute of Technology,
Aytekin A, Feyzmahdavian HR, Johansson M (2016) Analysis and implementation of an asynchronous optimization algorithm for the parameter server. arXiv preprint arXiv:1610.05507
Beck A (2017) First-order methods in optimization. SIAM
Beck A, Shtern S (2017) Linearly convergent away-step conditional gradient for non-strongly convex functions. Math Program 164(1–2):1–27
Beck A, Teboulle M (2009) A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imag Sci 2(1):183–202
Bolte J, Nguyen TP, Peypouquet J, Suter BW (2017) From error bounds to the complexity of first-order descent methods for convex functions. Math Program 165(2):471–507
Chretien S (2010) An alternating \( \ell _1 \) approach to the compressed sensing problem. IEEE Signal Process Lett 17(2):181–184
Combettes PL, Glaudin LE (2017) Quasi-nonexpansive iterations on the affine hull of orbits: from mann’s mean value algorithm to inertial methods. SIAM J Optim 27(4):2356–2380
Dn Blatt, Hero AO, Gauchman H (2007) A convergent incremental gradient method with a constant step size. SIAM J Optim 18(1):29–51
Drusvyatskiy D, Lewis AS (2013) Tilt stability, uniform quadratic growth, and strong metric regularity of the subdifferential. SIAM J Optim 23(1):256–267
Drusvyatskiy D, Lewis AS (2018) Error bounds, quadratic growth, and linear convergence of proximal methods. Math Oper Res 43(3):919–948
Felipe A, Hedy A (2001) An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal 9(1):3–11
Feyzmahdavian HR, Aytekin A and Johansson M (2014) A delayed proximal gradient method with linear convergence rate. In: 2014 IEEE international workshop on machine learning for signal processing (MLSP), pp 1–6. IEEE
Gurbuzbalaban M, Ozdaglar A, Parrilo PA (2017) On the convergence rate of incremental aggregated gradient algorithms. SIAM J Optim 27(2):1035–1048
Hale ET, Yin W and Zhang Z (2007) A fixed-point continuation method for \( \ell _1 \)-regularized minimization with applications to compressed sensing. CAAM TR07-07, Rice University, 43:44
Hoffman AJ (1952) On approximate solutions of systems of linear inequalities. J Res Natl Bur Stand 49(4):263–265
Jia Z, Huang J and Cai X (2021) Proximal-like incremental aggregated gradient method with bregman distance in weakly convex optimization problems. J Global Optim, 1–24
Jingwei L, Jalal F, Gabriel P (2016) A multi-step inertial forward-backward splitting method for non-convex optimization. In: Advances in neural information processing systems, pp 4035–4043
Johnstone PR, Moulin P (2017) Local and global convergence of a general inertial proximal splitting scheme for minimizing composite functions. Comput Optim Appl 67(2):259–292
László SC (2021) Convergence rates for an inertial algorithm of gradient type associated to a smooth non-convex minimization. Math Program 190(1):285–329
Latafat P, Themelis A, Ahookhosh M and Patrinos P (2021) Bregman Finito/MISO for nonconvex regularized finite sum minimization without lipschitz gradient continuity. arXiv preprint arXiv:2102.10312
Li G, Pong TK (2018) Calculus of the exponent of kurdyka-łojasiewicz inequality and its applications to linear convergence of first-order methods. Found Comput Math 18(5):1199–1232
Liu Yuncheng, Xia Fuquan (2021) Variable smoothing incremental aggregated gradient method for nonsmooth nonconvex regularized optimization. Optimization Letters, pages 1–18
Li M, Zhou L, Yang Z, Li A, Xia F, Andersen DG and Smola A (2013) Parameter server for distributed machine learning. In: Big Learning NIPS Workshop, 6, pp 2
Łojasiewicz S (1959) Sur le problème de la division. Studia Math 18:87–136
Łojasiewicz S (1958) Division d’une distribution par une fonction analytiquede variables réelles. Comptes Rendus Hebdomadaires Des Seances de l Academie Des Sciences 246(5):683–686
Meier L, Geer SV, Bühlmann P (2008) The group lasso for logistic regression. J Royal Stat Soc: Ser B (Stat Methodol) 70(1):53–71
Necoara I, Nesterov Y, Glineur F (2019) Linear convergence of first order methods for non-strongly convex optimization. Math Program 175(1):69–107
Nesterov Y (2013) Gradient methods for minimizing composite functions. Math Program 140(1):125–161
Ochs P (2018) Local convergence of the heavy-ball method and ipiano for non-convex optimization. J Optim Theory Appl 177(1):153–180
Ochs P, Brox T, Pock T (2015) ipiasco: inertial proximal algorithm for strongly convex optimization. J Math Imag Vision 53(2):171–181
Parikh N, Boyd S (2014) Proximal algorithms. Found Trends® Optim 1(3):127–239
Peng CJ, Lee KL, Ingersoll GM (2002) An introduction to logistic regression analysis and reporting. J Educ Res 96(1):3–14
Peng W, Zhang H, Zhang X (2019) Nonconvex proximal incremental aggregated gradient method with linear convergence. J Optim Theory Appl 183(1):230–245
Pock T, Sabach S (2016) Inertial proximal alternating linearized minimization (iPALM) for nonconvex and nonsmooth problems. SIAM J Imag Sci 9(4):1756–1787
Polyak BT (1964) Some methods of speeding up the convergence of iteration methods. USSR Comput Math Math Phys 4(5):1–17
Rockafellar R (1970) On the maximal monotonicity of subdifferential mappings. Pacific J Math 33(1):209–216
Scheinberg K, Goldfarb D, Bai X (2014) Fast first-order methods for composite convex optimization with backtracking. Found Comput Math 14(3):389–417
Simon N, Friedman J, Hastie T, Tibshirani R (2013) A sparse-group lasso. J Comput Graphical Stat 22(2):231–245
Vanli DN, Gurbuzbalaban M, Ozdaglar A (2018) Global convergence rate of proximal incremental aggregated gradient methods. SIAM J Optim 28(2):1282–1300
Wen B, Chen X, Pong TK (2017) Linear convergence of proximal gradient algorithm with extrapolation for a class of nonconvex nonsmooth minimization problems. SIAM J Optim 27(1):124–145
Yang Q, Liu Y, Chen T, Tong Y (2019) Federated machine learning: concept and applications. ACM Trans Intell Syst Technol (TIST) 10(2):1–19
Yu P, Li G, K PT (2021) Kurdyka-Łojasiewicz exponent via inf-projection. Found Comput Math, pp 1–47
Yurii N (2013) Introductory lectures on convex optimization: a basic course, volume 87. Springer Science & Business Media
Zhang H (2020) New analysis of linear convergence of gradient-type methods via unifying error bound conditions. Math Program 180(1):371–416
Zhang H, Dai Y, Guo L, Peng W (2021) Proximal-like incremental aggregated gradient method with linear convergence under Bregman distance growth conditions. Math Oper Res 46(1):61–81
Acknowledgements
We are really grateful to the anonymous referees and the associate editor for many useful comments, which allowed us to significantly improve the original presentation. This work is supported by the National Science Foundation of China (No.11971480), the Natural Science Fund of Hunan for Excellent Youth (No.2020JJ3038), and the Fund for NUDT Young Innovator Awards (No. 20190105).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs of Theorems and Lemmas
Appendix: Proofs of Theorems and Lemmas
Proof of Theorem 1. From Lemma 2, for all \( k \ge 0\) we have
By combining the inequality above with Lemma 3, we get
In order to apply Lemma 1, let \(V_k:=F(x_{k})-F^{*}\), \(\omega _k:=\Vert x_{k+1}-x_{k}\Vert ^2\), \(a := 1/(1+ \frac{\sigma \alpha }{8(2+\beta )}), \alpha _1 := 1, \alpha _2 := 0, b_1 := (\frac{1-2\beta }{4\alpha })a, b_2 := \frac{3\beta }{4\alpha }a, c := \frac{3L}{4}a, k_0 := \tau .\) Making this setting satisfy the required conditions of Lemma 1, we need the following inequalities to hold:
and
The first condition could be guaranteed by letting \(\beta < \min \left\{ \frac{16}{83}, \frac{1}{2} \right\} = \frac{16}{83} \), since
according to \(\alpha L \in (0,1]\) and \(\beta \in [0,1)\). The second condition is guaranteed by
In fact, with this bound (guarantee of the following first inequality), we can derive that
where the second inequality follows from \(\beta \ge 0\) and \(\alpha \sigma \le 1\). Hence, the second condition holds as well. Therefore, the claimed convergence follows from Lemma 1.
Proof of Theorem 2. Since \({\mathcal {X}}\) is a nonempty closed convex set, the projection point of z onto \({\mathcal {X}}\) is unique, denoted by \(z^{*}\). Note that \(F(x_k^{*})=F^{*}\). According to Lemma 4, we obtain
Since \(x_k^{*}\in {\mathcal {X}}\), by the definition of projection, it holds that
Now, in terms of the expression of the Lyapunov function \(\Psi \), we have
By using the quadratic growth condition, we obtain
and hence
with \(p+q=1, p, q \ge 0\). Picking \(p=\frac{1-\beta }{\alpha \mu +1-\beta },q=\frac{\alpha \mu }{\alpha \mu +1-\beta }\) and combining (13) and (14), we obtain
In order to apply Lemma 1, let \(V_k=\Psi (x_k)\), \(\omega _k=\Vert x_{k+1}-x_{k}\Vert ^2\), \(a = \frac{1}{\alpha \mu +1-\beta }, \alpha _1 := 1, \alpha _2 := 0, b_1= \frac{1}{2\alpha }\), \(b_2 = \frac{\beta }{2\alpha }\), \(c=\frac{L(\tau +1)}{2}\), \(k_0=\tau \); we need the parameters satisfy (5) and (6), that is
Since \(\alpha \le \frac{1}{L}\), if the parameters satisfy the following conditions
then we have that \(0< a < 1\), \(\frac{b_2}{a} \le b_1\) and
This indicates that (16) holds. Therefore, from Lemma 1. \(\Psi (x_k)\) converges linearly in the sense of (9). The results (10) and (11) directly follow from the definition of \(\Psi (x)\) and (9).
Proof of Lemma 1. Note that \(A=\alpha _1 a\) and \(B=\alpha _2 a^2\) in (5). The inequality (4) can be rewritten as:
By dividing both sides of (17) by \(a^{k+1}\) and summing the resulting inequality up from \(k=1\) to \(K(K \ge 1)\), we derive that
Since \(w_k=0(k<0), w_k \ge 0(k \ge 0)\) and \(a>0\), we get
Therefore, together (19) and (18), we have that
By condition (6), we obtain
that is \(\frac{V_{K+1}}{a^{K+1}} \le V_0 + \frac{V_1}{a}+ \frac{b_1\omega _0}{a}\) for \(K \ge 1\). Besides, we know \(V_1 \le V_1+aV_0+b_1\omega _0\). Therefore, for \(\forall K\ge 1\), we have
This completes the proof.
Proof of Lemma 2. By using the L-gradient Lipschitz continuity of f, we have
Together with the subgradient inequality of f,
we have
Since that \(x_{k+1}\) is the minimizer of the \(\frac{1}{\alpha }\)-strongly convex function:
where \( g_k =\sum _{n=1}^N \nabla f_n(x_{k-\tau _{k}^n}) \). We have
By combining (23) and (24), we derive that
where the inequality follows by the Cauchy-Schwartz inequality. Note that \(\Vert \nabla f(x_k) - g_k\Vert \le L \sum \limits _{j=(k-\tau )_+}^{k-1} \Vert x_{j+1} - x_j\Vert \). Then, by using the Cauchy-Schwartz inequality again, we have that
Hence
where the last inequality uses the bound \(\alpha \le \frac{1}{(\tau +1)L}\). Put \(x = x_k\) , for \(\forall k \ge 0 \); then we have
Proof of Lemma 3. Denote \(x_{k+1}^\prime = \text {prox}_h^\alpha (x_k - \alpha \nabla f(x_k))\). By using the firm nonexpansivity of the proximal map (please refer to Theorem 6.42 (Beck 2017) for understanding the firm nonexpansivity) implies
Take \(x=x_k -\alpha \nabla f(x_k)\) and \(y = x^{*} -\alpha \nabla f( x^{*})\) (obviously \( \text {prox}_h^\alpha (y) = x^{*}\)) into (25) to yield
which implies \( 0 \le \langle x_{k+1}^\prime -x^{*}, - x_{k+1}^\prime + x_k -\alpha \nabla f(x_k) + \alpha \nabla f( x^{*}) \rangle \) for all \( k \ge 0\). This inequality can be rewritten as follows:
where the second inequality is based on the negativeness of \(- \Vert x_{k+1}^\prime -x_k \Vert ^2 \) and the Cauchy-Schwartz inequality, the third inequality is according to the L-gradient Lipschitz continuity of f. Since \( \langle \nabla f(x_k) - \nabla f(x^{*}), x_k -x^{*} \rangle \ge \sigma \Vert x_k - x^{*}\Vert ^2\) due to the strong convexity of f and the condition \(\alpha L \le 1\), we obtain
Thus,
where the second inequality is according to the nonexpansive property of the proximal map \(\Vert \text {prox}_h^\alpha (x) - \text {prox}_h^\alpha (y) \Vert \le \Vert x-y\Vert \) for any \(x, y \in {\mathbb {R}}^d\). After rearranging the terms and multiplying two sides by \(\Vert x_{k+1} - x_k\Vert \), we obtain
The first term \( -\frac{\alpha \sigma }{2}\Vert x_k - x^{*}\Vert \Vert x_{k+1} - x_k\Vert \) of the right-hand side can be bounded as follows:
where we denote \(r_{k+1} \in \partial h(x_{k+1})\). Due to convexity of h and (23), we have \( \langle x_{k+1}-x^{*}, -\alpha r_{k+1}\rangle \le \alpha (h(x^{*}) - h(x_{k+1})) \) and \(f(x_{k+1}) - f(x^{*}) \le \langle \nabla f(x_k) , x_{k+1} - x^{*} \rangle + \frac{L}{2} \Vert x_{k+1} - x_k\Vert ^2\). Denote \(F_k := F(x_k)-F(x^{*})\); then we can derive that
where the last inequality is from (27). By combining (29) and (28), we get
Since \( \Vert \nabla f(x_k) - g_k\Vert \le L \sum \limits _{j=(k-\tau )_+}^{k-1} \Vert x_{j+1} - x_j\Vert \), we have that
and
Put (31), (32), and (30) together to yield
Since \(\alpha \le \frac{1}{(\tau +1)L}, 0 \le \beta < 1\), we have the following bounds
Hence, for \( k \ge 0\) it holds that
This completes the proof.
Proof of Lemma 4. Since each component function \(f_n(x)\) is convex with \(L_n\)-continuous gradient, we derive that
where the second inequality follows from the convexity of \(f_n(x)\). By summing (33) over all components functions and using the expression of \(g_k\), we have
Note that \(x_{k+1}\) is the minimizer of the \(\frac{1}{\alpha }\)-strongly convex function:
Then, we have
After rearranging the terms of (35), we further get
By combining (34) and (36), we derive that
According to the Jensen inequality, we obtain \(\sum _{n=1}^N\frac{L_n}{2}\Vert x_{k+1}-x_{k-\tau _k^n}\Vert _2^2 = \sum _{n=1}^N\frac{L_n}{2}\Vert x_{k+1}-x_{k}+ \cdots +x_{k+1-\tau _k^n} -x_{k-\tau _k^n}\Vert ^2 \le \frac{L(\tau +1)}{2}\sum _{j=(k-\tau )_+}^k\Vert x_{j+1}-x_{j}\Vert ^2\). Therefore, the desired inequality follows. This completes the proof.
Rights and permissions
About this article
Cite this article
Zhang, X., Peng, W. & Zhang, H. Inertial proximal incremental aggregated gradient method with linear convergence guarantees. Math Meth Oper Res 96, 187–213 (2022). https://doi.org/10.1007/s00186-022-00790-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-022-00790-0
Keywords
- Linear convergence
- Inertial method
- Quadratic growth condition
- Incremental aggregated gradient
- Lyapunov function