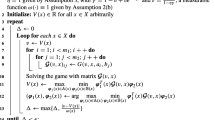Abstract.
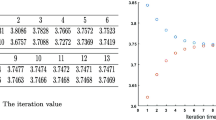
The goal of this paper is provide a theory of K-person non-stationary Markov games with unbounded rewards, for a countable state space and action spaces. We investigate both the finite and infinite horizon problems. We define the concept of strong Nash equilibrium and present conditions for both problems for which strong Nash or Nash equilibrium strategies exist for all players within the Markov strategies, and show that the rewards in equilibrium satisfy the optimality equations.
Similar content being viewed by others
Author information
Authors and Affiliations
Additional information
Manuscript received: November 1999/Final version received: March 2000
Rights and permissions
About this article
Cite this article
Jia, R., Ding, Y. Nonzero-sum non-stationary discounted Markov game model. Mathematical Methods of OR 52, 265–270 (2000). https://doi.org/10.1007/s001860000074
Issue Date:
DOI: https://doi.org/10.1007/s001860000074