Sensitivity analysis of a sequential decision problem with learning

Abstract.

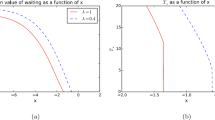
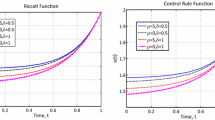
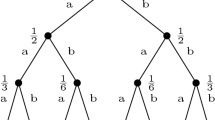
We consider the optimization problem of a decision maker facing a sequence of coin tosses with an initially unknown probability Θ for heads. Before each toss she bets on either heads or tails and she wins one euro if she guesses correctly, otherwise she loses one euro. We investigate the effect of changes in the distribution of Θ on the expected optimal gain of the decision maker. Using techniques from Bayesian dynamic programming we will show that under the assumption of a beta distribution for the prior a riskier prior implies higher expected gains. The rationale for this is that a riskier prior allows better learning and provides higher informational value to the observations. We will also consider the case of a risk-sensitive decision maker in a two-period model.