Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bayer, D., Stillman, M.: A criterion for detecting m-regularity. Invent. Math. 87(1), 1–11 (1987)
Bruns, W., Herzog, J.: Cohen-Macaulay rings. Cambridge University Press, 1993
Conca, A., Valla, G.: A property of lex-segment ideals. private notes, 1999
Cook, M.: The connectedness of space curves invariants. Compositio Math. 111, 221–244 (1998)
Eisenbud, D.: Commutative Algebra with a view towards Algebraic Geometry. Springer-Verlag, 1995
Eliahou, S., Kervaire, M.: Minimal resolution of some monomial ideals. J. Alg. 129, 1–25 (1990)
Galligo, A.: A propos du Théorem de Préparation de Weierstrass. L.N. Math. 409, 543–579 (1974)
Galligo, A.: Exemples d’ ensembles de points en position uniforme. E.M.A.G. (ed. by Mora, T., Traverso, C.) Progress in Mathematics 94, Birkhäuser, Boston, (1991), pp. 105–117
Geramita, A.V., Gregory, D., Roberts, L.: Monomial ideals and Points in Projective Space. J. Pure Appl. Alg. 40, 33–62 (1986)
Geramita, A.V. , Harima, T., Shin, L.Y.S.: An Alternative to the Hilbert Function for the Ideal of a Finite Set of Points in
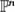 . Illinois J. of Math. (to appear)
. Illinois J. of Math. (to appear)Geramita, A.V., Harima, T., Shin, L.Y.S.: Extremal Point Sets and Gorenstein Ideals. Adv. Math. 152, 78–119 (2000)
Green, M.: Generic initial ideals. In: Six Lectures on Commutative Algebra (eds. Elias, J., Giral, J.M., Mirò-Roig, R.M., Zarzuela, S.), Progress in Mathematics 166, Birkhäuser, Boston, (1998), pp. 119–185
Hartshorne, R.: Connectedness of the Hilbert scheme. Math. I.H.E.S. 29, 261–304 (1966)
Macaulay, F.S.: Some properties of enumeration in the theory of modular systems. Proc. London Math. Soc. 26, 531–555 (1927)
Marinari, M.G., Mora, T., Möller, H.M.: Gröbner bases of ideals defined by functionals with an application to ideals of projective points. A. A. E. C. C. vol. 4, no. 2, 103–145 (1992)
Marinari, M.G., Ramella, L.: Some properties of Borel ideals. J. Pure Appl. Alg. (special issue MEGA 1998) 139, 183–200 (1999)
Marinari, M.G., Ramella, L.: Criteria for stability and Borelness. In: Zero-dimensional schemes and applications. Proceedings of the workshop Naples 2000, Queen’s Papers Pure Appl. Math. 123, (2002)
Zharkov, A. Yu.: Solving zero-dimensional involutive systems. In: Algorithms in Algebraic Geometry and Applications (eds. Gonzàlez-Vega, L., Recio, T.), Progress in Mathematics 143, Birkhäuser, Boston, (1996), pp. 389–399
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors were supported by MURST and GNSAGA(CNR)
Rights and permissions
About this article
Cite this article
Marinari, M., Ramella, L. A characterization of stable and Borel ideals. AAECC 16, 45–68 (2005). https://doi.org/10.1007/s00200-005-0171-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00200-005-0171-2


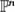 . Illinois J. of Math. (to appear)
. Illinois J. of Math. (to appear)