Skip to main content

Advertisement

Springer Nature Link
Log in

Elliptic curves and Fibonacci numbers arising from Lindenmayer system with symbolic computation

  • Published:
Applicable Algebra in Engineering, Communication and Computing Aims and scope

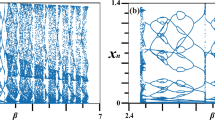
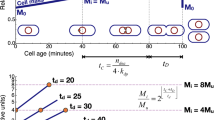
Abstract

Starting from an egg, the multicell becomes a set of cells comprising a variety of types to serve functions. This phenomenon brings us a bio-motivated Lindenmayer system. To investigate conditions for a variety of cell types, we have constructed a stochastic model over Lindenmayer systems. This model considers interactive behaviors among cells, yielding complicated polynomials. Using symbolic computation, we have derived explicit relations between cell-type diversity and cell-type ratio constraint. These relations exhibit elliptic curve- and Fibonacci number-related patterns. This is the first example of elliptic curves to appear in the Lindenmayer context. A survey of the rational points and the quadratic irrational numbers on the derived curves has revealed Fibonacci-related periodic and quasiperiodic patterns. Further we have found that in some region, there are only two elliptic curve-related periodic patterns.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P.: Molecular Biology of the Cell. 5th edn. Garland Science, New York (2008)

    Google Scholar 

  2. Bryant P.J., Bryant S.V., French V.: Biological regeneration and pattern formation. Sci. Am. 237, 67–81 (1977)

    Article  Google Scholar 

  3. Caviness B.F., Johnson J.R.: Quantifier Elimination and Cylindrical Algebraic Decomposition. Springer, Wien (1998)

    MATH  Google Scholar 

  4. Eichhorst P., Ruskey F.: On unary stochastic Lindenmayer systems. Inf. Control 48(1), 1–10 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  5. Eichhorst P., Savitch W.J.: Growth functions of stochastic Lindenmayer systems. Inf. Control 45(3), 217–228 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  6. French V.: Leg regeneration in the cockroach, Blattella germanica I. regeneration from a congruent tibial graft/host junction. Roux’s Arch. Dev. Biol. 179, 57–76 (1976)

    Google Scholar 

  7. French V., Bryant P.J., Bryant S.V.: Pattern regulation in epimorphic fields. Science 193, 969–980 (1976)

    Article  Google Scholar 

  8. Gilbert S.F.: Developmental Biology. 8th edn. Sinauer Associates, Sunderland (2006)

    Google Scholar 

  9. Jürgensen H., Lindenmayer A.: Inference algorithms for developmental systems with cell lineages. Bull. Math. Biol. 49(1), 93–123 (1987)

    MathSciNet  MATH  Google Scholar 

  10. Kaneko M., Odagaki T.: Selfsimilarity in a class of quadratic-quasiperiodic chains. J. Phys. Soc. Jpn. 62(4), 1147–1152 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  11. Koshy T.: Fibonacci and Lucas Numbers with Applications. Wiley, New York (2001)

    MATH  Google Scholar 

  12. Lindenmayer A.: Mathematical models for cellular interactions in development. I. filaments with one-sided inputs. J. Theor. Biol. 18(3), 280–299 (1968)

    Article  Google Scholar 

  13. Lindenmayer A.: Mathematical models for cellular interactions in development. II. simple and branching filaments with two-sided inputs. J. Theor. Biol. 18(3), 300–315 (1968)

    Article  Google Scholar 

  14. Mishra B.: Algorithmic Algebra. Springer, New York (1993)

    MATH  Google Scholar 

  15. Odagaki T., Kaneko M.: Self-similarity of binary quasiperiodic sequences. J. Phys. A: Math. Gen. 27, 1683–1690 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  16. Rozenberg G., Salomaa A.: The Mathematical Theory of L System. Academic Press, New York (1980)

    Google Scholar 

  17. Silverman J.H. (1986) The arithmetic of elliptic curves. In: Graduate Texts in Mathematics, vol. 106. Springer, New York

  18. Stroeker R.J., Tzanakis N.: Solving elliptic diophantine equations by estimating linear forms in elliptic logarithms. Acta Arith. 67, 165–190 (1994)

    MathSciNet  Google Scholar 

  19. Tzanakis N.: Solving elliptic diophantine equations by estimating linear forms in elliptic logarithms. the case of quartic equations. Acta Arith. 75, 165–190 (1996)

    MathSciNet  MATH  Google Scholar 

  20. Ványi, R., Kókai, G., Tóth, Z., Pető, T.: Grammatical retina description with enhanced methods. In: Poli, R., Banzhaf, W., Langdon, W.B., Miller, J.F., Nordin, P., Fogarty, T.C. (eds.) Genetic Programming, Proceedings of EuroGP, LNCS, vol. 1802, pp. 193–208. Springer, Berlin (2000)

  21. Yokomori, T.: Inductive inference of 0L languages. In: Lindenmayer systems: Impacts on Theoretical Computer Science, Computer Graphics, and Developmental Biology, chap. 2, pp. 115–132. Springer, Berlin (1992)

  22. Yoshida H., Anai H., Horimoto K.: Derivation of rigorous conditions for high cell–type diversity by algebraic approach. Biosystems 90, 486–495 (2007)

    Article  Google Scholar 

  23. Yoshida, H., Horimoto, K., Anai, H.: Inference of probabilities over a stochastic IL-system by quantifier elimination. In: Kotsireas, I. (ed.) Mathematics in Computer Science, Modeling and Analysis of Complex systems, vol. 1(3), pp. 473–485. Birkhäuser (2008)

  24. Yoshida H., Kaneko K.: Unified description of regeneration by coupled dynamical systems theory: intercalary/segmented regeneration in insect legs. Dev. Dyn. 238, 1974–1983 (2009)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics, Kyushu University, Itou, Motouoka 744, Nishi-ku, Fukuoka, 819-0395, Japan

    Hiroshi Yoshida & Masanobu Kaneko

  2. Graduate School of Comprehensive Human Sciences, University of Tsukuba, Tennoudai 1-1-1, Tsukuba-shi, Ibaraki, 305-8575, Japan

    Yoshihiro Miwa

Authors
  1. Hiroshi Yoshida
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yoshihiro Miwa
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Masanobu Kaneko
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hiroshi Yoshida.

Electronic Supplementary Material

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yoshida, H., Miwa, Y. & Kaneko, M. Elliptic curves and Fibonacci numbers arising from Lindenmayer system with symbolic computation. AAECC 22, 147–164 (2011). https://doi.org/10.1007/s00200-011-0143-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00200-011-0143-7

Keywords

Mathematics Subject Classification (2000)