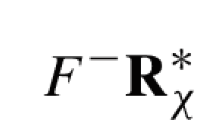De Nugis Groebnerialium 6: Rump, Ufnarovski, Zacharias

Abstract

Moved by a question posed us by Wolfgang Rump, we investigate the Rump ideal ${\mathbb {I}}(p^2-pq+qp)\subset {\mathbb {Z}}\langle q,q^{-1}, p\rangle$ and we show, this way, the power of Zacharias representation.

A Gebauer–Möller versus Buchberger criteria

As the reader can notice, our paper deals with Gröbner bases but we never talk about Buchberger algorithm and criteria. This appendix is devoted to explain the reasons of this choice in details.

The Lifting Theorem (Theorems 3 and 4) was originally implemented in most available softwares by Gebauer and Möller in the late eighties and formally described in [7]. Their approach, applied to ideals of the polynomial ring ${\mathbf {k}}[X_1,\ldots ,X_n]$ over a field ${\mathbf {k}}$, was proposing more efficient criteria than those proposed by Buchberger [2].

The survey [18] presented Buchberger Algorithm for the commutative polynomial ring ${\mathbf {k}}[X_1,\ldots ,X_n]$ and extended it for the free algebra ${\mathbf {k}}\langle X_1,\ldots ,X_n\rangle$ substituting the obsolete Buchberger Criteria with the more efficient criteria which were granted by Gebauer and Möller.

A formal statement of the Lifting Theorem was given by Möller⁶ [17] for polynomial rings $R[X_1,\ldots ,X_n]$ over a PIR R and extended by Pritchard [29, 30] to the free algebra $R\langle X_1,\ldots ,X_n\rangle$ over a PIR R.

In order to describe both Buchberger’s and Gebauer–Möller’s criteria, we need to introduce a further notation. Let us assume to have a finite sequence $G {:}{=} \{g_1,\ldots , g_s\}\subset {\mathbf {k}}[X_1,\ldots ,X_n]$ of polynomials; let us further assume, without loss of generality, that $\mathrm{lc}(g_1)=1$ for each i and define for each set $\{i_1,\ldots ,i_j\} \subset \{1,\cdots , s\}$

$$\begin{aligned} \mathbf{T}(i_1,\ldots ,i_j) {:}{=} \mathrm{lcm}(\mathbf{T}(g_{i_1}),\ldots,\mathbf{T}(g_{i_j})); \end{aligned}$$

in particular, for $i,j,k, 1 \le i,j,k \le s:$

$$\begin{aligned} \mathbf{T}(i)&{:}{=} \mathbf{T}(g_i), \\ \mathbf{T}(i,j)&{:}{=}\mathrm{lcm}(\mathbf{T}(g_i), \mathbf{T}(g_j)), \\ \mathbf{T}(i,j,k)&{:}{=}\mathrm{lcm}(\mathbf{T}(g_i), \mathbf{T}(g_j),\mathbf{T}(g_k)). \end{aligned}$$

For each pair $\{i,j\}, 1\le i < j\le s$ the related S-polynomial is $S(i,j) {:}{=} \frac{{\mathbf{T}(i,j)}}{{\mathbf{T}(j)}} g_j - \frac{{\mathbf{T}(i,j)}}{{\mathbf{T}(i)}} g_i.$

For each polynomial $f\in {\mathbf {k}}[X_1,\ldots ,X_n]$, NF(f, G) denotes some normal form of f w.r.t. G.

Lemma 17

(Buchberger’s First Criterion)

$$\begin{aligned} \mathbf{T}(i) \mathbf{T}(j) = \mathbf{T}(i,j) \,\Longrightarrow \,NF(S(i,j), G) = 0. \end{aligned}$$

Lemma 18

(Buchberger’s Second Criterion) For $i,j, 1 \le i < j \le s$, if there is $k, 1 \le k \le s$: $\mathbf{T}(k) \mid \mathbf{T}(i,j),$ and $NF(S(i,k), G) = NF(S(k,j), G) =0$ then also $NF(S(i,j), G) =0$.

Lemma 19

(Möller) For each $i,j,k : 1 \le i , j , k \le s$ it holds

$$\begin{aligned} \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,k)} S(i,k) - \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,j)} S(i,j) +\frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(k,j)} S(k,j)= 0. \end{aligned}$$

Proof

One has

$$\begin{aligned}&\frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,k)} S(i,k) - \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,j)} S(i,j) + \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(k,j)} S(k,j) \\ & = \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,k)} \left( \frac{{\mathbf{T}(i,k)}}{{\mathbf{T}(k)}} g_k - \frac{{\mathbf{T}(i,k)}}{{\mathbf{T}(i)}} g_i\right) \\ & \quad- \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,j)} \left( \frac{\mathbf{T}(i,j)}{{\mathbf{T}(j)}} g_j - \frac{\mathbf{T}(i,j)}{{\mathbf{T}(i)}} g_i\right) \\ & \quad + \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(k,j)} \left( {\frac{\mathbf{T}(k,j)}{{\mathbf{T}(j)}} g_j - \frac{{\mathbf{T}(k,j)}}{\mathbf{T}(k)}} g_k\right) \\ & = \left( \frac{{\mathbf{T}(i,j,k)}}{{\mathbf{T}(k)}} g_k - \frac{{\mathbf{T}(i,j,k)}}{{\mathbf{T}(i)}} g_i\right) \\ & \quad- \left( \frac{{\mathbf{T}(i,j,k)}}{{\mathbf{T}(j)}} g_j - \frac{{\mathbf{T}(i,j,k)}}{{\mathbf{T}(i)}} g_i\right) \\ & \quad+ \left( \frac{{\mathbf{T}(i,j,k)}}{{\mathbf{T}(j)}} g_j - \frac{{\mathbf{T}(i,j,k)}}{{\mathbf{T}(k)}} g_k\right) \\ & = 0 \end{aligned}$$

$\square$

If, in this equation relating three S-polynomials, at least one of the coefficients, say $\frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,j)}$, is 1, then the corresponding S-polynomial S(i, j) is a combination of the other two S-polynomials; therefore it is sufficient to prove that $NF(S(i,k), G) = NF(S(k,j), G) =0$ in order to deduce that also $NF(S(i,j), G) =0$. However, very often, all the three coefficients are constant and in order to avoid aporetic loops one must consider which one of the possible S-polynomials is to be considered as ‘useless’.

To do so, it is sufficient to impose on the set

$$\begin{aligned} \mathfrak {S}(s)=\{(i,j), 1\le i < j \le s\} \end{aligned}$$

any ordering $\prec$, which is compatible with the term-ordering < on ${\mathcal {T}}$, i.e.

$$\begin{aligned} \mathbf{T}(i_1,j_1) < \mathbf{T}(i_2,j_2) \,\Longrightarrow \,(i_1,j_1) \prec (i_2,j_2), \end{aligned}$$

and choose as ‘useless’ the biggest element among the possible choices. We will therefore impose on $\mathfrak {S}(s)$ the ordering $\prec$ defined by

$$\begin{aligned} (i_1,j_1) \prec (i_2,j_2) \iff {\left\{ \begin{array}{ll} \mathbf{T}(i_1,j_1)< \mathbf{T}(i_2,j_2)&{} \hbox { or }\\ \mathbf{T}(i_1,j_1) = \mathbf{T}(i_2,j_2), j_1< j_2&{} \hbox { or }\\ \mathbf{T}(i_1,j_1) = \mathbf{T}(i_2,j_2), j_1 = j_2, i_1 < i_2. &{} \\ \end{array}\right. } \end{aligned}$$

(1)

Let us assume that

$$\begin{aligned} (i,k) \prec (i,j), (j,k) \prec \{i,j\}\, (\Rightarrow j \ne k) \text{ and } \frac{\mathbf{T}(i,j,k)}{ \mathbf{T}(i,j)} = 1; \end{aligned}$$

therefore we have

$$\begin{aligned} \mathbf{T}(i,j,k) = \mathbf{T}(i,j), \mathbf{T}(k) \mid \mathbf{T}(i,j), \mathbf{T}(i,k) \mid \mathbf{T}(i,j), \mathbf{T}(j,k) \mid \mathbf{T}(i,j). \end{aligned}$$

There are now three possible cases according to the position of k:

B:

: $i< j < k$,

M:

: $i< k < j$,

F:

: $k< i < j$;

which behave as follows:

B:

: since $(i,k) \prec (i,j)$ and $k > j$ then $\mathbf{T}(i,k) \ne \mathbf{T}(i,j)$; similarly

$$\begin{aligned} (j,k) \prec (i,j), k > j \,\Longrightarrow \,\mathbf{T}(j,k) \ne \mathbf{T}(i,j); \end{aligned}$$

M:

: $(k,j) \prec (i,j), i < k \,\Longrightarrow \,\mathbf{T}(k,j) \ne \mathbf{T}(i,j)$;

F:

: $k< i < j$ then $\mathbf{T}(k,j) = \mathbf{T}(i,j)$;

This simple remark yields

Corollary 20

(Buchberger’s Second Criterion (strong)) For $i,j, 1 \le i < j \le s$, if there is $k, 1 \le k \le s$ such that

B:

$i< j < k$, $\mathbf{T}(k) \mid \mathbf{T}(i,j)$, $\mathbf{T}(i,k) \ne \mathbf{T}(i,j) \ne \mathbf{T}(j,k)$ or

M:

$k < j$, $\mathbf{T}(k,j) \mid \mathbf{T}(i,j) \ne \mathbf{T}(k,j)$ or

F:

$k< i < j$, $\mathbf{T}(k,j) = \mathbf{T}(i,j),$

then

$$\begin{aligned} S(i,j) = \frac{\mathbf{T}(i,j,k)}{\mathbf{T}(i,k)} S(i,k) + \frac{\mathbf{T}(i,j,k)}{\mathbf{T}(k,j)} S(k,j). \end{aligned}$$

If, moreover, $NF(S(i,k), G) = NF(S(k,j), G) =0$ then also $NF(S(i,j), G) =0$.

Since from the first implementations, it became clear that the bottleneck of Buchberger Algorithm was the efficiency of the normal form computations. This lead to Buchberger’s introduction of his criteria, to the informal notion of useless pairs and to investigate efficient strategies to apply Buchberger Criteria in order to detect useless pairs. As suggested by Buchberger, the most efficent way to apply his criteria required a ”fair strategy“⁷ [28] and he suggested (and Gebauer–Möller followed his suggestion) to select each time a minimal pair with respect to the used term-ordering; but this transferred the bottleneck of Buchberger Algorithm to the management of the set of the pairs. The results of Lemma 19 and Corollary 20 allowed Gebauer–Möller to devise the algorithm of Fig. 1 which guarantees the needed management of the set of the pairs in B, disposing of the corresponding bottleneck. The general algorithm is inductively performed for each element $g_i\in G, 1\le i\le s$ and allows to produce a Gebauer–Möller set for the input basis $G=\{g_1,\ldots , g_s\}$ and allows to modify it anytime a new element is added to the basis.

Fig. 1

Gebauer–Möller S-pair management

The correctness of the procedure can be argued as follows:

• The removal of elements from $\mathfrak {G}\mathfrak{M}_*$ is a direct consequence of Buchberger Second Criterion.

• For the generic element $S(i,s), i < s$, denote $\tau {:}{=} \mathbf{T}(i,s)$ and note that:

  • if there exists $\tau '\in \mathsf{T}$ such that $\mathbf{T}(i_{\tau '},s) = \tau ' \mid \mathbf{T}(i,s) \ne \tau '$, then since $i_{\tau '} < s$, then the correctness follows from case M of Corollary 20

  • if $i = i_\tau$ and $\mathbf{T}(i_\tau )\mathbf{T}(s) = \mathbf{T}(i_\tau ,s)$, the correctness follows from Buchberger’s First Criterion;

  • if $i = i_\tau$ and $\mathbf{T}(i_\tau )\mathbf{T}(s) \ne \mathbf{T}(i_\tau ,s)$ then $\{i_\tau ,s\}\in \mathfrak {G} \mathfrak{M}$;

  • if $i \ne i_\tau$ then

    $$\begin{aligned} S(i,s) = \frac{\mathbf{T}(i,i_\tau ,s)}{\mathbf{T}(i,i_\tau )} S(i,i_\tau ) + S(i_\tau ,s) \end{aligned}$$

    where $S(i,i_\tau )$ has the required term-bounded representation in terms of $\mathfrak {G} \mathfrak{M}_*$.

As it is stated in [4] where the Lifting Theorem was extended to effective rings over a PIR: it is well known that Buchberger test/completion is definitely superseded in each honest survey of Buchberger Theory and (what is more important) in all available implementations, by the test/completion based on the lifting theorem [17]: a generating set F is a Gröbner basis if and only if each element in a minimal basis of the syzygies among the leading monomials $\{\mathbf{M}(f_{\alpha }) : f_{\alpha }\in F\}$ lifts, via Buchberger reduction, to a syzygy among the elements of F.

The point is that the lifting theorem allowed Gebauer–Möller [7, 8] to give more efficient criteria. Thus they detect at least as many “useless” pairs as Buchberger’s two criteria [2], but they do not need to verify whether a pair satisfies the conditions required by the Second Criterion and thus they avoid the consequent bottleneck needed for listing and ordering the S-pairs (in the commutative case they are $(\#F)^2$ while a careful informal analysis in that setting suggests that the S-pairs needed by Gebauer–Möller Criterion are $n\#F$). Moreover, the flexibility of Möller lifting theorem approach - with respect to Buchberger S-pair test - allows the former to extend Buchberger theory verbatim at least to (non commutative) monoid rings over PIRs.

This drastic statement was supported by a careful analysis performed by the senior author and reported in a course given in Bangalore in 2010 [25, 26] (see also [24, II Ex.25.2.1]) of a non trivial case-study, where the computation of the Gröbner basis of the ideal of 3 binomials $\{g_1,g_2,g_3\}\in {\mathbf {k}}[X,Y,Z,W,V]$ in 5 variables under the lexicographical ordering < induced by $X<Y<Z<Y<U$ produce the following sequence of polynomials:

$$\begin{aligned} g_1&{:}{=}\mathbf{V^2}-XZ;\\ g_2&{:}{=}\mathbf{Y^2}-X^3;\\ g_3&{:}{=}\mathbf{YZV}-X^2W;\\ g_4&{:}{=}\mathbf{X^3ZV} - X^2YW;\\ g_5&{:}{=}\mathbf{X^2YVW} - X^4Z^2;\\ g_6&{:}{=}\mathbf{X^5VW} - X^4YZ^2;\\ g_7&{:}{=}\mathbf{X^4YW^2}- X^4YZ^3;\\ g_8&{:}{=}\mathbf{X^7W^2}- X^7Z^3;\\ g_9&{:}{=}\mathbf{X^4W^2}- X^4Z^3;\\ g_{10}&{:}{=}\mathbf{X^3YW^3}- X^3YZ^3W;\\ g_{11}&{:}{=}\mathbf{X^2WV} - XYZ^2;\\ g_{12}&{:}{=}\mathbf{X^2YW^2}- X^2YZ^3, \end{aligned}$$

the required basis being thus $\{g_1,g_2,g_3,g_4,g_9,g_{11},g_{12}\}.$

The results of these analysis is reported in the following table

Buchberger	2	3	4	5	6	7	8	9	10	11	12	#
useful			1	2	3	4	5	6	7	8	9
First Criterion									5	15	16	24
Second Criterion				2		3		4	5		6	11
useless					1		2		6	9	11	17
old S-pairs			2	1	4	6	11	15	12	7	12	0
actual S-pairs			5	5	9	12	18	23	21	17	23

Gebauer–Möller	2	3	4	5	6	7	8	9	10	11	12	#
useful			1	2	3	4	5	6	7	8	9
redundant								1		3
useless				1		2		3	7	10	12	18
old S-pairs		0	1	1	3	4	5	4	3	0	2	0
actual S-pairs	0	2	3	4	6	6	7	8	6	5	6

where, at each $s{th}$ iterative loop:

• for both algorithms

  • useful records the number of pairs computed and producing a new element up to that loop; obviously in each loop the value increases by 1;

  • useless records the number of pairs computed and reduced to 0 up to that loop; we have decided to write a value only if at that loop a computation is performed;

  • old S-pairs records the number of pairs present in the list when the new element $g_s$ is added to the basis;

  • actual S-pairs records the number of pairs present in the list after the inclusion of the necessary S-pairs (i, s); of course, for Buchberger Algorithm, the difference between actual S-pairs and old S-pairs is $s-1$;

  • the last column, marked #, records all the data including the pairs dealt after the last basis element is computed and the final verification that the output basis is Gröbner.

• For Buchberger Algorithm

  • First Criterion and Second Criterion record the number of pairs removed up to that loop by applyng the Criterion; we have decided to write a value only if at that loop a new application occurs.

• For Gebauer–Möller

  • redundant records the number of pairs up to that loop removed from $\mathfrak {G} \mathfrak{M}_*$ as a direct consequence of Buchberger Second Criterion.

What is relevant is that both algorithms compute in the same ordering the same “useful” S-pair producing the same polynomial; the difference is based on the pair storage: Buchberger criteria approach requires to store up to 23 elements, while the Gebauer–Möller set approach stores at most 8 elements while Buchberger criteria approach stores always at least 8 elements after the third loop introducting $g_6$.