Skip to main content
Springer Nature Link
Log in

Asymptotic expansions and numerical algorithms of eigenvalues and eigenfunctions of the Dirichlet problem for second order elliptic equations in perforated domains

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Summary.

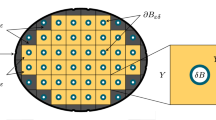
In this paper, we study the spectral properties of Dirichlet problems for second order elliptic equation with rapidly oscillating coefficients in a perforated domain. The asymptotic expansions of eigenvalues and eigenfunctions for this kind of problem are obtained, and the multiscale finite element algorithms and numerical results are proposed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adams, R.A.: Sobolev Spaces, Acad. Press, New York- San Francisco- London, 1975

  2. Bensoussan, A., Lions, J.L., Papanicolaou, G.: Asymptotic Analysis of Periodic Structures. North-Holland, Amsterdam, 1978

  3. Bourgat, J.F.: Numerical experments to the homogenization method for operators with periodic coefficients. Lect. Notes in Math. 705, 1977, 330–356, Springer-verlag, 1979

    Google Scholar 

  4. Cao, L.Q., Cui, J.Z., Huang, Y.: Finite element computation for elastic structures of composite materials formed by entirely basic configuration. Chinese J. Num. Math. & Appl., Allerton Press Inc. 20(4), 25–37 (1998)

    Google Scholar 

  5. Ciarlet, P.G.: The finite Element Method for Elliptic Problems. North-Holland, Amsterdam, 1978

  6. Cioranescu, D., Donato, P.: An Introduction to Homogenization. Oxford University Press, New York, 1999

  7. Cioranescu, D., Jean Paulin, J.S.: Homogenization of Reticulated Structures. Springer-Verlag, New York, 1998

  8. Courant, R., Hilbert, D.: Methods of Mathematical Physics. Vol. I, New york, Interscience, 1953

  9. Cui, J.Z., Yang, H.Y.: Dual coupled method of boundary value problems of PDE with coefficients of small period. J. Comp. Math. 18(3), 157–174 (1996)

    Google Scholar 

  10. Egorov, E., Kondratiev, V.: On Spectral Theory of Elliptic Operator. Birkhauser Verlag, Berlin, 1996

  11. Hou, T.Y., Wu, X.H., Cai, Z.: Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients. Math. Comp. 68, 913–943 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hou, T.Y., Wu, X.H.: A multiscale finite element method for elliptic problems in composite materials and porous media. J. Comp. Phys. 134, 169–189 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  13. Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations of Second Order (2nd ed). Springer-Verlag, Berlin and New York, 1983

  14. Gilbarg, D., Hörmander, L.: Intermediate Schauder Estimates, Archiev for Rational Mechanics and Analysis 74, 297–318 (1980)

    Google Scholar 

  15. Grisvard, P.: Behavior of the solutions of an elliptic boundary value problem in a polygonal or polyhedral domain, Numerical Solution of Partial Differential Equations-III (B. Hubbard Editor) Academic Press, New York, 1976, pp. 207–274

  16. Jikov, V.V., Kozlov, S.M., Oleinik, O.A.: Homogenization of Differential Operators and Integral Functionals. Springer-Verlag, Beilin, 1994

  17. Kardestuncer, H., Norrie, D.H.: Finite Element Handbook. McGraw-Hill Book Company, 1987

  18. Kesavan, S.: Homogenization of elliptic eigenvalue problems. Part I, Appl. Math. Optim. 5, 153–167 (1979)

    Google Scholar 

  19. Kesavan, S.: Homogenization of elliptic eigenvalue problems. Part II, Appl. Math. Optim. 5, 197–216 (1979)

    Google Scholar 

  20. Qun, L., Zhu, Q.D.: The Preprocessing and Postprocessing for the Finite Element Method, Shanghai Scientific & Technical Publishers. 1994 (in Chinese)

  21. Lions, J.L.: Some Methods for the Mathematical Analysis of Systems and Their Controls. Science Press, Beijing, 1981

  22. Lions, J.L.: Remarques sur I’homogeneisation, Computing Methods in Applied Sciences and Engineering, VI, INRIA, Amsterdam: North Holland, 299–315 (1984)

  23. Moskow, S., Vogelius, M.: First-order corrections to the homogenised eigenvalues of a periodic composite medium, A convergence proof. Proc. Of the Royal Society of Edinburgh 127A, 1263–1299 (1997)

    MathSciNet  MATH  Google Scholar 

  24. Oleinik, O.A., Shamaev, A.S., Yosifian, G.A.: Mathematical Problems in Elasticity and Homogenization. North-Holland, Amsterdam, 1992

  25. Pao, Y.H., Mow, C.C.: Diffraction of Elastic Waves and Dynamic Stress Concentrations. Crane, Russak & Company Inc. in US, 1973

  26. Quarteroni, A., Valli, A.: Numerical approximation of partial differential equations. Springer-Verlag, 1997

  27. Santosa, F., Vogelius, M.: First-order corrections to homogenized eigenvalues of a periodic composite medium. SIAM J. Appl. Math. 53(6), 1636–1668 (1993)

    MATH  Google Scholar 

  28. Walker, J.S.: Fourier Analysis, Oxford University Press. New York, Oxford, 1988

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Mathematics and Science-Engineering Computing, The Academy of Mathematics and System Sciences, The Chinese Academy of Sciences, P.O.Box 2719, Beijing, 100080, P.R.China

    Li-Qun Cao

  2. Institute of Computational Mathematics and Science-Engineering Computing, The Academy of Mathematics and System Sciences, The Chinese Academy of Sciences, P.O.Box 2719, Beijing, 100080, P.R.China

    Jun-Zhi Cui

Authors
  1. Li-Qun Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jun-Zhi Cui
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Li-Qun Cao.

Additional information

Mathematics Subject Classification (2000): 65F10, 35P15

This work is Supported by National Natural Science Foundation of China (grant # 19932030) and Special Funds for Major State Basic Research Projects (grant # TG2000067102)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Cao, LQ., Cui, JZ. Asymptotic expansions and numerical algorithms of eigenvalues and eigenfunctions of the Dirichlet problem for second order elliptic equations in perforated domains. Numer. Math. 96, 525–581 (2004). https://doi.org/10.1007/s00211-003-0468-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-003-0468-7

Keywords