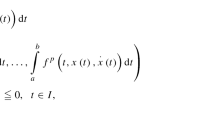Skip to main content
SpringerLink
Log in

Linear-programming approach to nonconvex variational problems

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Summary.

In nonconvex optimization problems, in particular in nonconvex variational problems, there usually does not exist any classical solution but only generalized solutions which involve Young measures. In this paper, after reviewing briefly the relaxation theory for such problems, an iterative scheme leading to a “sequential linear programming” (=SLP) scheme is introduced, and its convergence is proved by a Banach fixed-point technique. Then an approximation scheme is proposed and analyzed, and calculations of an illustrative 2D “broken-extremal” example are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anderson, H., Lebech, B., Poulse, H.F.: The structural phase diagram and oxygen equilibrium partial pressure of Y B2Cu3O6+x studied by powder diffraction and gas volumetry. Phys. C 172, 31–42 (1990)

    Google Scholar 

  2. Ball, J.M.: A version of the fundamental theorem for Young measures. Partial differential equations and continuum models of phase transitions. M. Rascle, D. Serre, M. Slemrod (eds.), Lecture Notes in Physics 344, 207–215 (1989)

    Google Scholar 

  3. Ball, J.M., Kirchheim, B., Kristensen, J.: Regularity of quasiconvex envelopes. Calc. Var. Partial Differ. Equ. 11(4), 333–359 (2000)

    Article  MATH  Google Scholar 

  4. Bartels, S.: Adaptive approximation of young measure solutions in scalar non-convex variational problems. SIAM J. Numer. Anal. 42 (5), 505–529 (2004)

    Article  Google Scholar 

  5. Bartels, S.: Numerical analysis of some non-convex variational problems. PhD-Thesis. Christian–Albrechts–Universität zu Kiel, Kiel 2001, (Available online at http://e-diss.uni-kiel.de/diss_519/)

  6. Bartels, S., Carstensen, C., Dolzmann, G.: Inhomogenous Dirichlet conditions in a priori and a posteriori finite element error analysis. Numer. Math. (published online) (2004). DOI: 10.1007/s00211-004-0548-3

  7. Brighi, B., Chipot, M.: Approximated convex envelope of a function. SIAM J. Numer. Anal. 31, 128–148 (1994)

    MATH  Google Scholar 

  8. Carstensen, C.: Numerical analysis of microstructure. Lecture Notes No. 10, Max-Planck-Institute for Mathematics in the Sciences, Leipzig, 2001

  9. Carstensen, C., Bartels, S.: Each averaging technique yields reliable a posteriori error control in FEM on unstructured grids. Part I: Low order conforming, nonconforming, and mixed FEM. Math. Comp. 71(239), 945–969 (2002)

    Google Scholar 

  10. Carstensen, C., Jochimsen, K.: Adaptive finite element methods for micro-structures? Numerical experiments for a 2-well benchmark. Computing 71(2) 175–204 (2003)

    Google Scholar 

  11. Carstensen, C., Plecháč, P.: Numerical solution of the scalar double-well problem allowing microstructure. Math. Comp. 66, 997–1026 (1997)

    Article  MATH  Google Scholar 

  12. Carstensen, C., Plecháč, P.: Numerical analysis of compatible phase transitions in elastic solids. SIAM. J. Numer. Anal. 37, 2061–2081 (2000)

    Article  MATH  Google Scholar 

  13. Carstensen, C., Roubíček, T.: Numerical approximation of Young measures in nonconvex variational problems. Numer. Math. 84, 395–415 (2000)

    Article  MATH  Google Scholar 

  14. Chipot, M.: Numerical analysis of oscillations in conconvex problems. Numer. Math. 59, 747–767 (1991)

    MATH  Google Scholar 

  15. Chipot, M.: The use of Young measures for constructing minimizing sequences in the calculus of variations. J. Appl. Anal. 1, 71–81 (1995)

    MATH  Google Scholar 

  16. Chipot, M., Collins, C.: Numerical approximations in variational problems with potential wells. SIAM J. Numer. Anal. 29, 1002–1019 (1992)

    MATH  Google Scholar 

  17. Chipot, M., Collins, C., Kinderlehrer, D.: Numerical analysis of oscillations in multiple well problems. Numer. Math. 70, 259–282 (1995)

    Article  MATH  Google Scholar 

  18. DeSimone, A.: Energy minimizers for large ferromagnetic bodies. Arch. Rat. Mech. Anal. 125, 99–143 (1993)

    Article  Google Scholar 

  19. Fletcher, R., Sainz de la Maza, E.: Nonlinear programming and nonsmooth optimization by sequential linear programming. Math. Prog. 43, 235–256 (1989)

    MATH  Google Scholar 

  20. Friesecke, G.: A necessary and sufficient conditions for nonattainment and formation of microstructure almost ewerywhere in scalar variational problems. Proc. Royal Soc. Edinburgh 124A, 437–471 (1994)

    MATH  Google Scholar 

  21. Goodman, J., Kohn, R.V., Reyna, L.: Numerical study of a relaxed variational problem from optimal design. Comput. Methods Appl. Mech. Engrg. 57, 107–127 (1986)

    Article  MATH  Google Scholar 

  22. Govindjee, S., Mielke, A., Hall, G.J.: Free-energy of mixing for n-variant martensitic phase transformations using quasi-convex analysis. J. Mech. Physics Solids 50, 1897–1922 (2002)

    Article  MATH  Google Scholar 

  23. Griewank, A., Rabier, P.J.: On the smoothness of convex envelopes. Trans. A.M.S. 322(2), 691–709 (1990)

    MATH  Google Scholar 

  24. Horgan, C.O.: Anti-plane shear deformation in linear and nonlinear solid mechnaics. SIAM Review 1995, pp. 53–81

  25. Kinderlehrer, D., Pedregal, P.: Gradient Young measures generated by sequences in Sobolev spaces. J. Geom. Anal. 4, 59–90 (1994)

    MATH  Google Scholar 

  26. Kohn, R.: The relaxation of a double-well energy. Contin. Mech. Thermodyn. 3, 193–236 (1991)

    MATH  Google Scholar 

  27. Kružík, M.: Numerical approach to double-well problem. SIAM J. Numer. Anal. 35, 1833–1849 (1998)

    Article  Google Scholar 

  28. Kružík, M.: Maximum principle based algorithm for hysteresis in micromagnetics. Adv. Math. Sci. Appl. 13(2), 461–485 (2003)

    Google Scholar 

  29. Kružík, M., Prohl, A.: Young measures approximation in micromagnetics, Numer. Math. 90, 291–307 (2001)

    Google Scholar 

  30. Luskin, M.: On the computation of crystalline microstructure. Acta Numerica 5, 191–257 (1996)

    MATH  Google Scholar 

  31. Mach, J.: Numerical solution of a class of nonconvex variational problems by SQP. Numer. Funct. Anal. Optim. 23, 573–587 (2002)

    Article  MATH  Google Scholar 

  32. Mataché, A.-M., Roubíček, T., Schwab, C.: Higher-order convex approximations of Young measures in optimal control. Adv. Comput. Math. Adv. Comput. Math. 19, 158–167 (2003)

    Google Scholar 

  33. Meziat, R.: Analysis of two dimensional non convex variational problems. In: Qi, Teo, and Yang (eds.), Optimization and control with applications. Kluwer

  34. Nicolaides, R.A., Walkington, N.J.: Computation of microstructure utilizing Young measure representations. In: C.A. Rogers, R.A. Rogers, (eds.), Recent Advances in Adaptive and Sensory Materials and their Applications. Technomic Publ. Lancaster, 1992, pp. 131–141

  35. Nicolaides, R.A., Walkington, N.J.: Strong convergence of numerical solutions to degenerate variational problems. Math. Comp. 64, 117–127 (1995)

    Article  MATH  Google Scholar 

  36. Osborne, M.R., Womersley, R.S.: Strong uniqueness in sequential linear programming. J. Aust. Math. Soc. B 31, 379–384 (1990)

    MATH  Google Scholar 

  37. Pedregal, P.: Numerical approximation of parametrized measures. Numer. Funct. Anal. Opt. 16, 1049–1066 (1995)

    MATH  Google Scholar 

  38. Pedregal, P.: On the numerical analysis of non-convex variational problems. Numer. Math. 74, 325–336 (1996)

    Article  MATH  Google Scholar 

  39. Pedregal, P.: Parametrized Measures and Variational Principles. Basel, Birkäuser, 1997

  40. Roubíček, T.: Approximation theory for generalized Young measures. Numer. Funct. Anal. Opt. 16, 1233–1253 (1995)

    Google Scholar 

  41. Roubíček, T.: Numerical approximation of relaxed variational problems. J. Convex Anal. 3, 329–347 (1996)

    Google Scholar 

  42. Roubíček, T.: Relaxation in Optimization Theory and Variational Calculus. W. de Gruyter, Berlin, New York, 1997

  43. Roubíček, T., Kružík, M.: Adaptive approximation algorithm for relaxed optimization problems. In: K.-H. Hoffmann, R.H.W. Hoppe, V. Schultz, (eds.), Proc. Conf. Fast solution of discretized optimization problems ISNM 138, Birkhäuser, Basel, 2001 pp. 242–254

  44. Roubíček, T., Šverák, V.: Nonexistence of solutions in nonconvex multidimensional variational problems. J. Convex Anal. 7, 427–436 (2000)

    Google Scholar 

  45. Showalter, R.E.: Monotone Operators in Banach Spaces and Nonlinear Partial Differential Equations. AMS, Providence, 1997

  46. Swart, P.J., Holmes, P.J.: Energy minimization and the fomration of microstructure in dynamic anti-plane shear. Arch. Rat. Mech. Anal. 121, 37–85 (1992)

    Article  MATH  Google Scholar 

  47. Verfürth, R.: A Review of A Posteriori Error Estimation and Adaptive Mesh-Refinement Techniques. Wiley-Teubner, 1996

  48. Smyshlyaev, V.P., Willis, J.R.: On the relaxation of a three-well energy. Proc. Royal Soc. London A 455, 779–814 (1999)

    MATH  Google Scholar 

  49. Zhang, J., Kim, N.E., Lasdon, L.: An Improved Successive Linear Programming Algorithm. Management Science 31, 1312–1331 (1985)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Maryland, College Park, MD, 20742, USA

    Sören Bartels

  2. Mathematical Institute, Charles University, Sokolovská 83, 186 75, Praha 8, Czech Republic

    Tomáš Roubíček

  3. Institute of Information Theory and Automation, Academy of Sciences, Pod vodárenskou věží 4, 182 08, Praha 8, Czech Republic

    Tomáš Roubíček

Authors
  1. Sören Bartels
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tomáš Roubíček
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sören Bartels.

Additional information

Mathematics Subject Classification (2000): 49M05, 65K10, 65N30

Acknowledgement S.B. gratefully acknowledges support by the DFG through the priority program 1095 “Analysis, Modeling and Simulation of Multiscale Problems” while T.R.’s research was partly covered by the grants A 107 5005 (GA AV ČR), and MSM 11320007 (MŠMT ČR).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bartels, S., Roubíček, T. Linear-programming approach to nonconvex variational problems. Numer. Math. 99, 251–287 (2004). https://doi.org/10.1007/s00211-004-0549-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-004-0549-2

Keywords

Search

Navigation