Skip to main content
Springer Nature Link
Log in

Hybrid cross approximation of integral operators

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

The efficient treatment of dense matrices arising, e.g., from the finite element discretisation of integral operators requires special compression techniques. In this article we use the -matrix representation that approximates the dense stiffness matrix in admissible blocks (corresponding to subdomains where the underlying kernel function is smooth) by low-rank matrices. The low-rank matrices are assembled by a new hybrid algorithm (HCA) that has the same proven convergence as standard interpolation but also the same efficiency as the (heuristic) adaptive cross approximation (ACA).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bebendorf, M.: Approximation of boundary element matrices. Numer. Math. 86(4), 565–589 (2000)

    Google Scholar 

  2. Bebendorf, M., Rjasanov, S.: Adaptive Low-Rank Approximation of Collocation Matrices. Computing 70(1), 1–24 (2003)

    Article  Google Scholar 

  3. Börm, S.: Approximation of integral operators by 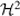-matrices with adaptive bases. Preprint 18, Max Planck Institute for Mathematics in the Sciences, 2004. To appear in Computing

  4. Börm, S., Grasedyck, L.: HLib – a library for - and 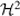-matrices, 1999. Available at http://www.hlib.org/

  5. Börm, S., Grasedyck, L.: Low-rank approximation of integral operators by interpolation. Computing 72, 325–332 (2004)

    Google Scholar 

  6. Börm, S., Grasedyck, L., Hackbusch, W.: Introduction to hierarchical matrices with applications. Engineering Analysis with Boundary Elements 27, 405–422 (2003)

    Article  Google Scholar 

  7. Börm, S., Hackbusch, W.: Data-sparse approximation by adaptive 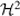-matrices. Computing 69, 1–35 (2002)

    Article  Google Scholar 

  8. Börm, S., Hackbusch, W.: 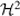-matrix approximation of integral operators by interpolation. Applied Numerical Mathematics 43, 129–143 (2002)

    Article  MathSciNet  Google Scholar 

  9. Dahmen, W., Schneider, R.: Wavelets on manifolds I: Construction and domain decomposition. SIAM Journal of Mathematical Analysis 31, 184–230 (1999)

    Article  Google Scholar 

  10. Ronald A. DeVore, George G. Lorentz.: Constructive Approximation. Springer-Verlag, 1993

  11. Ford, J.M., Tyrtyshnikov, E.E.: Combining kronecker product approximation with discrete wavelet transforms to solve dense, function-related linear systems. SIAM J. Sci. Comput. 25(3), 961–981 (2003)

    Article  Google Scholar 

  12. Goreinov, S.A., Tyrtyshnikov, E.E., Zamarashkin, N.L.: A theory of pseudoskeleton approximations. Lin. Alg. Appl. 261, 1–22 (1997)

    Google Scholar 

  13. Grasedyck, L.: Theorie und Anwendungen Hierarchischer Matrizen. Doctoral thesis, Universität Kiel, 2001

  14. Grasedyck, L.: Adaptive recompression of -matrices for BEM. Technical report 17, Max Planck Institute for Mathematics in the Sciences, 2004.

  15. Grasedyck, L., Hackbusch, W.: Construction and arithmetics of -matrices. Computing 70(4), 295–334 (2003)

    Article  Google Scholar 

  16. Greengard, L., Rokhlin, V.: A new version of the fast multipole method for the Laplace in three dimensions. In: Acta Numerica 1997, Cambridge University Press, 1997, pp. 229–269

  17. Hackbusch, W.: A sparse matrix arithmetic based on -matrices. Part I: Introduction to -matrices. Computing 62, 89–108 (1999)

    Article  Google Scholar 

  18. Hackbusch, W., Khoromskij, B.: A sparse matrix arithmetic based on -matrices. Part II: Application to multi-dimensional problems. Computing 64, 21–47 (2000)

    Google Scholar 

  19. Hackbusch, W., Nowak, Z.P.: On the fast matrix multiplication in the boundary element method by panel clustering. Numerische Mathematik 54, 463–491 (1989)

    Article  Google Scholar 

  20. Rivlin, T.J.: The Chebyshev Polynomials. Wiley-Interscience, New York, 1984

  21. Rokhlin, V.: Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 60, 187–207 (1985)

    Article  Google Scholar 

  22. Sauter, S.: Variable order panel clustering (extended version). Technical report 52, Max-Planck-Institut für Mathematik, Leipzig, Germany, 1999

  23. Tyrtyshnikov, E.: Incomplete cross approximation in the mosaic-skeleton method. Computing (64), 367–380 (2000)

Download references

Author information

Authors and Affiliations

  1. Max-Planck-Institute for Mathematics in the Sciences, Inselstrasse 22–26, 04103, Leipzig, Germany

    Steffen Börm & Lars Grasedyck

Authors
  1. Steffen Börm
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Lars Grasedyck
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Steffen Börm.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Börm, S., Grasedyck, L. Hybrid cross approximation of integral operators. Numer. Math. 101, 221–249 (2005). https://doi.org/10.1007/s00211-005-0618-1

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-005-0618-1

Mathematics Subject Classification (2000)