Abstract
We study numerical integration 
for functions f with singularities. Nonadaptive methods are inefficient in this case, and we show that the problem can be efficiently solved by adaptive quadratures at cost similar to that for functions with no singularities.
Consider first a class 
of functions whose derivatives of order up to r are continuous and uniformly bounded for any but one singular point. We propose adaptive quadratures Q*
n
, each using at most n function values, whose worst case errors 
are proportional to n−r. On the other hand, the worst case error of nonadaptive methods does not converge faster than n−1.
These worst case results do not extend to the case of functions with two or more singularities; however, adaption shows its power even for such functions in the asymptotic setting. That is, let F∞ r be the class of r-smooth functions with arbitrary (but finite) number of singularities. Then a generalization of Q* n yields adaptive quadratures Q** n such that |I(f)−Q** n (f)|=O(n−r) for any f ∈ F∞ r . In addition, we show that for any sequence of nonadaptive methods there are `many' functions in F∞ r for which the errors converge no faster than n−1.
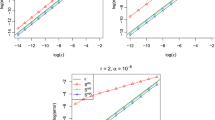
Results of numerical experiments are also presented.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Atkinson, K.E.: An Introduction to Numerical Analysis. 2nd ed., Wiley, New York, 1989
Bakhvalov, N.S.: On the optimality of linear methods for the operator approximation in convex classes of functions (in Russian), Zh. Vychisl. Mat. Mat. Fiz. 11, 1014–1018 (1971)
Cheney, W., Kincaid, D.: Numerical Mathematics and Computing. 4th ed., Brooks/Cole, New York, 1999
Conte, S.D., de Boor, C.: Elementary Numerical Analysis – An Algorithmic Approach. 3rd ed., McGraw-Hill, New York, 1980
Corman, T.H., Leiserson, C.E., Rivest, R.L.: Introduction to Algorithms. MIT Press, 1990
Davis, P.J., Rabinowitz, P.: Methods of Numerical Integration. Academic Press, New York, 1975
de Boor, C., CADRE: An algorithm for numerical quadrature. Mathematical Software, Academic Press, New York, 201–209 (1971)
Gal S., Micchelli, C.A.: Optimal sequential and non-sequential procedures for evaluating a functional. Appl. Anal. 10, 105–120 (1980)
Huerta, I.: Adaption helps for some nonconvex classes. J. Complexity 2, 333–352 (1986)
Kiefer, J.: Optimum sequential search and approximation methods under minimum regularity assumption. J. Soc. Indust. Appl. Math. 5, 105–136 (1957)
Krommer, A.R., Ueberhuber, C.W.: Computational Integration. SIAM, Philadelphia, 1998
Lyness, J.M.: Notes on the adaptive Simpson quadrature routine. J. Assoc. Comput. Mach. 16, 483–495 (1969)
McKeeman, W.M.: Algorithm 145, adaptive numerical integration by Simpson's rule. Comm. ACM 5, 604 (1962)
Novak, E.: Quadrature formulas for convex classes of functions. In: Numerical Integration IV (H. Brass and G. Hämmerlin, eds), ISNM 112, Birkhäuser, Basel, 1993, pp. 283–296
Novak, E.: On the power of adaption. J. Complexity 12, 199–238 (1996)
Piessens, R., deDoncker-Kapenga, E., Überhuber, C., Kahaner, D.: QUADPACK: A Subroutine Package for Automatic Integration. Springer Verlag, New York, 1983
Plaskota, L.: Noisy Information and Computational Complexity. Cambridge University Press, Cambridge, 1996
Ralston, A., Rabinowitz, P.: A First Course in Numerical Analysis. 2nd ed., McGraw-Hill, New York, 1978
Rice, J.R.: A metalgorithm for adaptive quadrature. J. Assoc. Comput. Mach. 22, 61–82 (1975)
Traub, J.F., Wasilkowski, G.W., Woźniakowski, H.: When is nonadaptive information as powerful as adaptive information? Proceedings of the 23rd IEEE Conference on Decision and Control, San Diego, 1984, pp. 1536–1540
Traub, J.F., Wasilkowski, G.W., Woźniakowski, H.: Information-Based Complexity. Academic Press, New York, 1988
Traub, J.F., Woźniakowski, H.: A General Theory of Optimal Algorithms. Academic Press, New York, 1980
Trojan, G.M.: Asymptotic Setting for Linear Problems. unpublished Ph.D. dissertation, 1980; results presented in [21, Sect. 2, Chapt. 10].
Wasilkowski, G.W.: Information of varying cardinality. J. Complexity 1, 107–117 (1986)
Wasilkowski, G.W., Gao, F.: On the power of adaptive information for functions with singularities. Math. Comp. 58, 285–304 (1992)
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors were partially supported, respectively, by the State Committee for Scientific Research of Poland under Project 1 P03A 03928 and by the National Science Foundation under Grant CCR-0095709.
Rights and permissions
About this article
Cite this article
Plaskota, L., Wasilkowski, G. Adaption allows efficient integration of functions with unknown singularities. Numer. Math. 102, 123–144 (2005). https://doi.org/10.1007/s00211-005-0640-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-005-0640-3