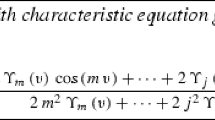Skip to main content
Springer Nature Link
Log in

A numerical method for computing the Hamiltonian Schur form

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

We derive a new numerical method for computing the Hamiltonian Schur form of a Hamiltonian matrix \({\mathcal{M}\in \mathbb{R}^{2n\times 2n}}\) that has no purely imaginary eigenvalues. We demonstrate the properties of the new method by showing its performance for the benchmark collection of continuous-time algebraic Riccati equations. Despite the fact that no complete error analysis for the method is yet available, the numerical results indicate that if no eigenvalues of \({\mathcal{M}}\) are close to the imaginary axis then the method computes the exact Hamiltonian Schur form of a nearby Hamiltonian matrix and thus is numerically strongly backward stable. The new method is of complexity \({\mathbf{O}(n^{3})}\) and hence it solves a long-standing open problem in numerical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ammar G.S., Mehrmann V. (1991): On Hamiltonian and symplectic Hessenberg forms. Linear Algebra Appl. 149, 55–72

    Article  MathSciNet  Google Scholar 

  2. Ammar G.S., Benner P., Mehrmann V. (1993): A multishift algorithm for the numerical solution of algebraic Riccati equations. Electr. Trans. Numer. Anal. 1, 33–48

    MathSciNet  Google Scholar 

  3. Arnold, W.F., III, Laub, A.J.: Generalized eigenproblem algorithms and software for algebraic Riccati equations. Proc. IEEE 72, 1746–1754 (1984)

  4. Benner, P., Kressner, D.: Fortran 77 subroutines for computing the eigenvalues of Hamiltonian matrices II. Submitted. See also http://www.math.tu-berlin.de/~kressner/hapack/ (2004)

  5. Benner, P., Laub, A., Mehrmann, V.: A collection of benchmark examples for the numerical solution of algebraic Riccati equations I: Continuous-time case. Technical Report SPC 95_22, Fak. f. Mathematik, TU Chemnitz–Zwickau, 09107 Chemnitz, FRG. http://www.mathematik. tu-chemnitz.de (1995)

  6. Benner P., Laub A.J., Mehrmann V. (1997): Benchmarks for the numerical solution of algebraic Riccati equations. IEEE Contr. Syst. Mag. 7, 18–28

    Article  Google Scholar 

  7. Benner P., Mehrmann V., Xu H. (1997): A new method for computing the stable invariant subspace of a real Hamiltonian matrix. J. Comput. Appl. Math. 86, 17–43

    Article  MathSciNet  Google Scholar 

  8. Benner P., Mehrmann V., Xu H. (1998): A numerically stable, structure preserving method for computing the eigenvalues of real Hamiltonian or symplectic pencils. Numer. Math. 78(3):329–358

    Article  MathSciNet  Google Scholar 

  9. Benner P., Mehrmann V., Xu H. (1999): A note on the numerical solution of complex Hamiltonian and skew-Hamiltonian eigenvalue problems. Electr. Trans. Numer. Anal. 8, 115–126

    MathSciNet  Google Scholar 

  10. Benner P., Mehrmann V., Xu H. (2002): Perturbation analysis for the eigenvalue problem of a formal product of matrices. BIT 42(1): 1–43

    Article  MathSciNet  Google Scholar 

  11. Benner, P., Kreß ner, D.: HAPACK, software for (skew-)Hamiltonian eigenvalue problems (2003)

  12. Bojanczyk A., Golub G.H., Van Dooren P. (1992): The periodic Schur decomposition; algorithms and applications. Proc. SPIE Conf. 1770, 31–42

    Google Scholar 

  13. Bora, S., Mehrmann, V.: Perturbation theory for structured matrix pencils arising in control theory. SIAM J. Matrix Anal. Appl. (2006) (to appear)

  14. Bunch J.R. (1987): The weak and strong stability of algorithms in numerical algebra. Linear Algebra Appl. 88, 49–66

    Article  MathSciNet  Google Scholar 

  15. Bunse-Gerstner, A., Byers, R., Mehrmann, V.: Numerical methods for algebraic Riccati equations. In: Bittanti, S. (ed.) Proc. Workshop on the Riccati Equation in Control, Systems, and Signals pp. 107–116. Como, Italy (1989)

  16. Bunse-Gerstner A., Mehrmann V. (1986): A symplectic QR-like algorithm for the solution of the real algebraic Riccati equation. IEEE Trans. Automat. Control AC-31, 1104–1113

    Article  MathSciNet  Google Scholar 

  17. Byers, R.: Hamiltonian and symplectic algorithms for the algebraic Riccati equation. PhD thesis, Cornell University, Dept. Comp. Sci., Ithaca (1983)

  18. Byers R. (1986): A Hamiltonian QR-algorithm. SIAM J. Sci. Statist. Comput 7, 212–229

    Article  MathSciNet  Google Scholar 

  19. Chu, D., Liu, X., Mehrmann, V.: A numerically backwards stable method for computing the Hamiltonian schur form. Preprint 2004/24. url: http://www.math.tu-berlin.de/preprints/

  20. Demmel J.W. (1987): Three methods for refining estimates of invariant subspaces. Computing 38, 43–57

    Article  MathSciNet  Google Scholar 

  21. Freiling G., Mehrmann V., Xu H. (2002): Existence, uniqueness and parametrization of Lagrangian invariant subspaces. SIAM J. Matrix Anal. Appl. 23, 1045–1069

    Article  MathSciNet  Google Scholar 

  22. Golub G.H., Van Loan C.F. (1996): Matrix Computations, 3rd edn. Johns Hopkins University Press, Baltimore

    MATH  Google Scholar 

  23. Hench J.J., Laub A.J. (1994): Numerical solution of the discrete-time periodic Riccati equation. IEEE Trans. Automat. Control 39, 1197–1210

    Article  MathSciNet  Google Scholar 

  24. Higham N.J. (1996): Accuracy and Stability of Numerical Algorithms. SIAM Publications, Philadelphia

    MATH  Google Scholar 

  25. Abou Kandil H., Freiling G., Ionescu V., Jank G. (2003): Matrix Riccati Equations in Control and Systems Theory. Birkhäuser, Verlag, Basel

    MATH  Google Scholar 

  26. Konstantinov M.M., Mehrmann V., Petkov P.Hr. (2002): Perturbation analysis for the Hamiltonian Schur form. SIAM J. Matrix Anal. Appl. 23, 387–424

    Article  MathSciNet  Google Scholar 

  27. Kreßner, D.: Numerical methods and software for general and structured eigenvalue problems. PhD thesis, TU Berlin, Institut für Mathematik, Berlin (2004)

  28. Kreßner D. (2004): The periodic QR algorithm is a disguised QR algorithm. Linear Algebra Appl. 417, 423–433

    Article  Google Scholar 

  29. Kressner D. (2005): Perturbation bounds for isotropic invariant subspaces of skew-Hamiltonian matrices. SIAM J. Matrix Anal. Appl. 26(4): 947–961

    Article  MathSciNet  Google Scholar 

  30. Lancaster P., Rodman L. (1995): The Algebraic Riccati Equation. Oxford University Press, Oxford

    Google Scholar 

  31. Laub, A.J.: A Schur method for solving algebraic Riccati equations. IEEE Trans. Automat. Control AC-24, 913–921 (1979) (See also Proc. 1978 CDC (Jan. 1979) pp. 60–65).

    Google Scholar 

  32. Laub A.J. (1991): Invariant subspace methods for the numerical solution of Riccati equations. In: Bittanti S., Laub A.J., Willems J.C. (eds) The Riccati Equation. Springer, Berlin Heidelberg New York, pp. 163–196

    Google Scholar 

  33. Lin, W.-W., Mehrmann, V., Xu, H.: Canonical forms for Hamiltonian and symplectic matrices and pencils. Linear Algebra Appl. 301–303, 469–533 (1999)

    Google Scholar 

  34. The MathWorks, Inc., Cochituate Place, 24 Prime Park Way, Natick, Mass, 01760. MATLAB Version 6.5 (2002)

  35. Mehrmann V. (1991): The Autonomous Linear Quadratic Control Problem, Theory and Numerical Solution. Lecture Notes in Control and Information Sciences, vol. 163. Springer, Berlin Heidelberg New York

    Book  MATH  Google Scholar 

  36. Mehrmann V., Watkins D. (2001): Structure-preserving methods for computing eigenpairs of large sparse skew-hamiltonian/hamiltonian pencils. SIAM J. Sci. Comput. 22, 1905–1925

    Article  MathSciNet  Google Scholar 

  37. Paige C.C., Van Loan C.F. (1981): A Schur decomposition for Hamiltonian matrices. Linear Algebra Appl. 14, 11–32

    Article  Google Scholar 

  38. Ran A.C.M., Rodman L. (1988): Stability of invariant Lagrangian subspaces I. In: Gohberg I. (eds) Operator Theory: Advances and Applications vol. 32. Birkhäuser-Verlag, Basel, pp. 181–218

    Google Scholar 

  39. Ran A.C.M., Rodman L. (1989): Stability of invariant Lagrangian subspaces II. In: Dym H.,S., Kaashoek M.A., Lancaster P. (eds) Operator Theory: Advances and Applications vol 40. Birkhäuser-Verlag, Basel, pp. 391–425

    Google Scholar 

  40. Sreedhar J., Van Dooren P. (1994): Periodic Schur forms and some matrix equations. Systems Netw. Math. Theory Appl. 77, 339–362

    Google Scholar 

  41. Stewart G.W. (1976): Simultaneous iteration for computing invariant subspaces of non Hermitian matrices. Numer. Math. 25, 123–136

    Article  Google Scholar 

  42. Van Dooren P. (1981): A generalized eigenvalue approach for solving Riccati equations. SIAM J. Sci. Statist. Comput. 2, 121–135

    Article  MathSciNet  Google Scholar 

  43. Van Loan C.F. (1984): A symplectic method for approximating all the eigenvalues of a Hamiltonian matrix. Linear Algebra Appl. 16, 233–251

    Article  Google Scholar 

  44. Van Loan C.F. (1985): Computing the CS and the generalized singular value decomposition. Numer. Math. 46, 479–491

    Article  MathSciNet  Google Scholar 

  45. Watkins, D.S.: On the reduction of a hamiltonian matrix to hamiltonian schur form. Preprint, Washington State University, Pullman 2005. http://www.sci.wsu.edu/math/faculty/watkins/ refpub.html. Elect. Trans. Numer. Anal. 23, 141–157 (2006)

  46. Xu, H.: Solving algebraic Riccati equations via Skew-Hamiltonian matrices. PhD thesis, Inst. of Math., Fudan University, Shanghai (1993)

  47. Xu H., Lu L. (1995): Properties of a quadratic matrix equation and the solution of the continuous-time algebraic Riccati equation. Linear Algebra Appl. 222, 127–146

    Article  MathSciNet  Google Scholar 

  48. Zhou K., Doyle J.C., Glover K. (1995): Robust and Optimal Control. Prentice-Hall, Upper Saddle River

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National University of Singapore, Science Drive 2, Singapore, 117543, Singapore

    Delin Chu

  2. Department of Electrical and Computer Engineering, University of Virginia, Charlottesville, VA, 22904-4743, USA

    Xinmin Liu

  3. Institut für Mathematik MA 4-5, TU Berlin, Straße des 17. Juni 136, 10623, Berlin, Germany

    Volker Mehrmann

Authors
  1. Delin Chu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xinmin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Volker Mehrmann
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Volker Mehrmann.

Additional information

Volker Mehrmann was supported by Deutsche Forschungsgemeinschaft, Research Grant Me 790/11-3.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chu, D., Liu, X. & Mehrmann, V. A numerical method for computing the Hamiltonian Schur form. Numer. Math. 105, 375–412 (2007). https://doi.org/10.1007/s00211-006-0043-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-006-0043-0

Mathematics Subject Classification