Skip to main content
Springer Nature Link
Log in

Mathematical and numerical study of a corrosion model

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

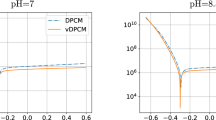
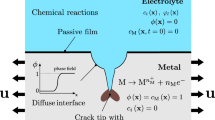
In this paper, we consider a PDE system arising in corrosion modelling. This system consists in two convection-diffusion equations on the densities of charge carriers and a Poisson equation on the electric potential. Boundary conditions are Robin boundary conditions. We discretize each equation by a finite volume scheme and we prove the convergence of the scheme towards a weak solution to the initial system. Finally, we provide numerical results describing the behaviour of the solutions with respect to an applied voltage.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alabau F.: New uniqueness theorems for the one-dimensional drift-diffusion semiconductor device equations. SIAM J. Math. Anal. 26(3), 715–737 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alabau F.: Structural properties of the one-dimensional drift-diffusion models for semiconductors. Trans. Am. Math. Soc. 348(3), 823–871 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  3. Alabau F.: Uniqueness results for the steady-state electrodiffusion equations in the case of monotonic potentials and multiple junctions. Nonlinear Anal. 29(8), 849–887 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  4. Alabau F.: On the existence of multiple steady-state solutions in the theory of electrodiffusion. I. The nonelectroneutral case. II. A constructive method for the electroneutral case. Trans. Am. Math. Soc. 350(12), 4709–4756 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bataillon, C., Chainais, C., Desgranges, C., Perrin, S., Tupin, M.: Corrosion modelling of iron based alloy in nuclear waste repository. Electrochem. Acta (2008, submitted)

  6. Chainais-Hillairet C., Peng Y.-J.: Convergence of a finite-volume scheme for the drift-diffusion equations in 1D. IMA J. Numer. Anal. 23, 81–108 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chainais-Hillairet C., Liu J.-G., Peng Y.-J.: Finite volume scheme for multi-dimensional drift-diffusion equations and convergence analysis. M2AN 37, 319–338 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chainais-Hillairet C., Peng Y.-J.: Finite volume approximation for degenerate drift-diffusion system in several space dimensions. Math. Models Methods Appl. Sci. 14, 461–481 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  9. Eymard R., Gallouët T., Herbin R. Finite Volume Methods. Handbook of numerical analysis, vol. VII. pp. 713–1020. North-Holland, Amsterdam (2000)

  10. Gajewski H.: On existence, uniqueness and asymptotic behavior of solutions of the basic equations for carrier transport in semiconductors. Z. Angew. Math. Mech 65(2), 101–108 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  11. Jüngel, A.: Quasi-hydrodynamic semiconductor equations. Progress in Nonlinear Differential Equations and their Applications, vol. 41, pp. x+293. Birkhäuser Verlag, Basel (2001)

  12. Markowich P.A.: The stationary semiconductor device equations, pp. ix+193. Springer, Vienna (1986)

    Google Scholar 

  13. Markowich P.A., Ringhofer C.A., Schmeiser C.: Semiconductor equations, pp. x  +  248. Springer, Heidelberg (1990)

    Google Scholar 

  14. Mock, M.S.: Analysis of mathematical models of semiconductor devices, pp. viii+200. Boole Press, Advances in Numerical Computation Series, n°3 (1983)

  15. Newman J., Thomas-Alyea K.E. (2004) Electrochemical systems, 3rd edn. Wiley, New York, pp. 672

    Google Scholar 

  16. Scharfetter D.L., Gummel H.K.: Large signal analysis of a silicon read diode oscillator. IEEE Trans. Electron Dev. 16, 64–77 (1969)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire de Mathématiques, UMR CNRS 6620, Université Blaise Pascal, 63177, Aubière Cedex, France

    Claire Chainais-Hillairet

  2. CEA/DEN/DANS/DPC/SCCME/LECA, 91191, Gif sur Yvette Cedex, France

    Christian Bataillon

Authors
  1. Claire Chainais-Hillairet
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Christian Bataillon
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Claire Chainais-Hillairet.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chainais-Hillairet, C., Bataillon, C. Mathematical and numerical study of a corrosion model. Numer. Math. 110, 1–25 (2008). https://doi.org/10.1007/s00211-008-0154-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-008-0154-x

Mathematics Subject Classification (2000)