Skip to main content
Springer Nature Link
Log in

Sliding motion on discontinuity surfaces of high co-dimension. A construction for selecting a Filippov vector field

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

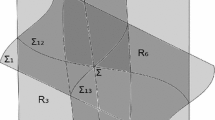
In this paper we consider the issue of sliding motion in Filippov systems on the intersection of two or more surfaces. To this end, we propose an extension of the Filippov sliding vector field on manifolds of co-dimension p, with p ≥ 2. Our model passes through the use of a multivalued sign function reformulation. To justify our proposal, we will restrict to cases where the sliding manifold is attractive. For the case of co-dimension p = 2, we will distinguish between two types of attractive sliding manifold: “node-like” and “spiral-like”. The case of node-like attractive manifold will be further extended to the case of p ≥ 3. Finally, we compare our model to other existing methodologies on some examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Acary V., Brogliato B.: Numerical methods for nonsmooth dynamical systems. Applications in Mechanics and Electronics, Lecture Notes in Applied and Computational Mechanics. Springer, Berlin (2008)

    Google Scholar 

  2. Alexander J.C., Seidman T.: Sliding modes in intersecting switching surfaces, I: Blending. Houston J. Math. 24, 545–569 (1998)

    MathSciNet  MATH  Google Scholar 

  3. Aubin J.-P., Cellina A.: Differential inclusions. Springer, Berlin (1984)

    MATH  Google Scholar 

  4. Bartolini G., Ferrara A.: A switching controller for systems with hard uncertainties. IEEE Trans. Circuits Syst. I 50, 984–990 (2003)

    Article  MathSciNet  Google Scholar 

  5. Bartolini G., Pisano A., Punta E., Usai E.: A survey of applications of second-order sliding mode control mechanical systems. Int. J. Control 76, 875–892 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  6. Batt G., Rogers D., de Jong H., Geiselmann J.: Qualitative analysis and verification of hybrid models of genetics regulatory networks: Nutritional stress response in escherichia coli. In: Morari, M., Thiele, L. (eds) HSCC, LNCS., pp. 134–150. Springer, Berlin (2005)

    Google Scholar 

  7. Boiko I.: Discontinuous Control Systems. Birkhauser, Boston (2009)

    MATH  Google Scholar 

  8. Brogliato, B.: Implicit euler numerical simulation of sliding mode systems. In: Conference SDS 2010. http://www.dm.uniba.it/~delbuono/sds10/LectureBrogliatoSDS2010.pdf

  9. Casey R., de Jong H., Gouze J.-L.: Piecewise-linear models of genetics regulatory networks: Equilibria and their stability. J. Math. Biol. 52, 27–56 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Corradini M.L., Orlando G.: Linear unstable plants with saturating actuators: robust stabilization by a time varying sliding surface. Automatica 43, 88–94 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  11. Davila J., Fridman L., Levant A.: Second order sliding mode observers for mechanical systems. IEEE Trans. Autom. Control 50, 1785–1789 (2005)

    Article  MathSciNet  Google Scholar 

  12. de Jong H., Gouze J.-L., Hernandez C., Page M., Sari T., Geiselmann J.: Qualitative simulation of genetic regulatory networks using piecewise-linear models. Bull. Math. Biol. 66, 301–340 (2004)

    Article  MathSciNet  Google Scholar 

  13. de Jong H., Gouze J.-L., Hernandez C., Sari T., Geiselmann J.: Dealing with discontinuities in the qualitative simulation of genetic regulatory network. In: Harmelen, F. (ed.) Proceedings of the 15th European Conference on Artificial Intelligence., pp. 725–730. IOS Press, Amsterdam (2002)

    Google Scholar 

  14. di Bernardo M., Budd C.J., Champneys A.R., Kowalczyk P.: Piecewise-smooth Dynamical Systems. Theory and Applications, Applied Mathematical Sciences 163. Springer-Verlag, Berlin (2008)

    Google Scholar 

  15. Dieci, L., Guglelmi, N.: Regularization methods for discontinuous differential equations

  16. Dieci L., Lopez L.: Sliding motion in Filippov differential systems: Theoretical results and a computational approach. SIAM J. Numer. Anal. 47, 2023–2051 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Edwards C., Spurgeron S.K.: Sliding Mode Control: Theory and Applications. Taylor and Francis, New York (1998)

    Google Scholar 

  18. Filippov A.F.: Differential Equations with Discontinuous Right-Hand Sides, Mathematics and Its Applications. Kluwer Academic, Dordrecht (1988)

    Google Scholar 

  19. Fridman L., Levant A.: Higher order sliding modes. In: Barbot, J.P., Perruguetti, W. (eds) Sliding Mode Control in Engineering., pp. 263–293. Marcel Dekker, New York (2002)

    Google Scholar 

  20. Fusco G., Guglielmi N.: A regularization for discontinuous differential equations with application to state-dependent delay differential equations of neutral. J. Differ. Equ. 250, 3230–3279 (2011)

    Article  Google Scholar 

  21. Galvanetto U.: Computational techniques for nonlinear dynamics in multiple frictions oscillators. Comput. Methods Appl. Mech. Eng. 163, 373–382 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  22. Galvanetto U.: Non-linear dynamics of multiple frictions oscillators. Comput. Methods Appl. Mech. Eng. 178, 291–306 (1999)

    Article  MATH  Google Scholar 

  23. Gouze J.-L., Sari T.: A class of piecewise linear differential equations arsing in biological models. Dyn. Syst. 17, 299–319 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  24. Johansson K.H., Rantzer A., Astrom K.J.: Fast swiyches in relay feedback systems. Automatica 35, 539–552 (1999)

    Article  MATH  Google Scholar 

  25. Leine R.I.: Bifurcations of equilibria in mechanical systems. Physica D 223, 121–137 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  26. Leine R.I., van Campen D.H.: Discontinuous fold bifurcations in non-smooth dynamical systems. Arch. Appl. Mech. 72, 138–146 (2002)

    Article  MATH  Google Scholar 

  27. Leine R.I., van Campen D.H., van de Vrande B.L.: Bifurcations in nonlinear discontinuous systems. Nonlinear Dyn. 23, 105–164 (2000)

    Article  MATH  Google Scholar 

  28. Llibre J., da Silva P.R., Teixeira M.A.: Regularization of discontinuous vector fields via singular perturbation. J. Dyn. Differ. Equ. 19, 309–331 (2009)

    Article  Google Scholar 

  29. Llibre J., da Silva P.R., Teixeira M.A.: Studies of singularities of nonsmooth dynamical systems via singular perturbation. SIAM J. Appl. Dyn. Syst. 8, 508–526 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. Sotomayor, J., Teixeira, M.A.: Regularization of discontinuous vector field. In: International Conference on Differential Equations, pp. 207–223, (1996)

  31. Stewart D.E.: A high accuracy method for solving ODEs with discontinuity right-hand side. Numer. Math. 58, 299–328 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  32. Stewart D.E.: Rigid-body dynamics with friction and impact. SIAM Rev. 42, 3–39 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  33. Utkin V.I.: Sliding Modes and Their Application in Variable Structure Systems. MIR Publisher, Moskow (1978)

    MATH  Google Scholar 

  34. Utkin V.I.: Sliding Mode in Control and Optimization. Springer, Berlin (1992)

    Google Scholar 

  35. Utkin V.I., Chang H.-C.: Sliding mode control on electro-mechanical systems. Math. Probl. Eng. 8, 451–473 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Georgia Institute of Technology, Atlanta, GA, 30332, USA

    Luca Dieci

  2. Dip. di Matematica, Universitá di Bari, Via Orabona 4, 70125, Bari, Italy

    Luciano Lopez

Authors
  1. Luca Dieci
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Luciano Lopez
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Luciano Lopez.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dieci, L., Lopez, L. Sliding motion on discontinuity surfaces of high co-dimension. A construction for selecting a Filippov vector field. Numer. Math. 117, 779–811 (2011). https://doi.org/10.1007/s00211-011-0365-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-011-0365-4

Mathematics Subject Classification (2000)