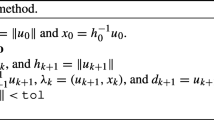Skip to main content
Springer Nature Link
Log in

An optimal adaptive FEM for eigenvalue clusters

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

The analysis of adaptive finite element methods in practice immediately leads to eigenvalue clusters which requires the simultaneous marking in adaptive finite element methods. A first analysis for multiple eigenvalues of the recent work Dai et al. (arXiv Preprint 1210.1846v2, 2013) introduces an adaptive method whose marking strategy is based on the element-wise sum of local error estimator contributions for multiple eigenvalues. This paper proves the optimality of a practical adaptive algorithm based on a lowest-order conforming finite element method for eigenvalue clusters for the eigenvalues of the Laplace operator in terms of nonlinear approximation classes. All estimates are explicit in the initial mesh-size, the eigenvalues and the cluster width to clarify the dependence of the involved constants.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Babuška, I., Osborn, J.: Eigenvalue problems. In: Handbook of numerical analysis, vol. II, Handb. Numer. Anal., II, pp. 641–787. North-Holland, Amsterdam (1991)

  2. Bank, R.E., Grubišić, L., Ovall, J.S.: A framework for robust eigenvalue and eigenvector error estimation and Ritz value convergence enhancement. Appl. Numer. Math. 66, 1–29 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  3. Binev, P., Dahmen, W., DeVore, R.: Adaptive finite element methods with convergence rates. Numer. Math. 97(2), 219–268 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  4. Boffi, D.: Finite element approximation of eigenvalue problems. Acta Numer. 19, 1–120 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  5. Braess, D.: Finite elements, 3rd edn. Cambridge University Press, Cambridge (2008)

    Google Scholar 

  6. Carstensen, C., Gallistl, D., Schedensack, M.: Adaptive nonconforming Crouzeix-Raviart FEM for eigenvalue problems. Math. Comp. (2014). doi:10.1090/S0025-5718-2014-02894-9

  7. Carstensen, C., Gedicke, J.: An oscillation-free adaptive FEM for symmetric eigenvalue problems. Numer. Math. 118(3), 401–427 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  8. Carstensen, C., Gedicke, J.: An adaptive finite element eigenvalue solver of quasi-optimal computational complexity. SIAM J. Numer. Anal. 50(3), 1029–1057 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  9. Carstensen, C., Gedicke, J.: Guaranteed lower bounds for eigenvalues. Math. Comp. 83(290), 2605–2629 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  10. Carstensen, C., Peterseim, D., Schedensack, M.: Comparison results of finite element methods for the Poisson model problem. SIAM J. Numer. Anal. 50(6), 2803–2823 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  11. Cascon, J., Kreuzer, C., Nochetto, R.H., Siebert, K.G.: Quasi-optimal convergence rate for an adaptive finite element method. SIAM J. Numer. Anal. 46(5), 2524–2550 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  12. Dai, X., He, L., Zhou, A.: Convergence rate and quasi-optimal complexity of adaptive finite element computations for multiple eigenvalues (2013, preprint). arXiv:1210.1846v2

  13. Dai, X., Xu, J., Zhou, A.: Convergence and optimal complexity of adaptive finite element eigenvalue computations. Numer. Math. 110(3), 313–355 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  14. Durán, R.G., Padra, C., Rodríguez, R.: A posteriori error estimates for the finite element approximation of eigenvalue problems. Math. Models Methods Appl. Sci. 13(8), 1219–1229 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  15. Evans, L.C.: Partial differential equations, graduate studies in mathematics, vol. 19, 2nd edn. American Mathematical Society, providence (2010)

    Book  Google Scholar 

  16. Garau, E.M., Morin, P.: Convergence and quasi-optimality of adaptive FEM for Steklov eigenvalue problems. IMA J. Numer. Anal. 31(3), 914–946 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  17. Garau, E.M., Morin, P., Zuppa, C.: Convergence of adaptive finite element methods for eigenvalue problems. Math. Models Methods Appl. Sci. 19(5), 721–747 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  18. Giani, S., Graham, I.G.: A convergent adaptive method for elliptic eigenvalue problems. SIAM J. Numer. Anal. 47(2), 1067–1091 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  19. Grubišić, L., Ovall, J.S.: On estimators for eigenvalue/eigenvector approximations. Math. Comp. 78(266), 739–770 (2009)

    MATH  MathSciNet  Google Scholar 

  20. Gudi, T.: A new error analysis for discontinuous finite element methods for linear elliptic problems. Math. Comp. 79(272), 2169–2189 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  21. Knyazev, A.V., Osborn, J.E.: New a priori FEM error estimates for eigenvalues. SIAM J. Numer. Anal. 43(6), 2647–2667 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  22. Liu, X., Oishi, S.: Verified eigenvalue evaluation for the Laplacian over polygonal domains of arbitrary shape. SIAM J. Numer. Anal. 51(3), 1634–1654 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  23. Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comp. 54(190), 483–493 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  24. Stevenson, R.: Optimality of a standard adaptive finite element method. Found. Comput. Math. 7(2), 245–269 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  25. Stevenson, R.: The completion of locally refined simplicial partitions created by bisection. Math. Comput. 77(261), 227–241 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  26. Strang, G., Fix, G.J.: An analysis of the finite element method. Prentice-Hall Series in Automatic Computation. Prentice-Hall Inc., Englewood Cliffs (1973)

    Google Scholar 

  27. Verfürth, R.: A review of a posteriori error estimation and adaptive mesh-refinement techniques. Advances in numerical mathematics. Wiley, New York (1996)

    Google Scholar 

Download references

Acknowledgments

The author would like to thank Professor C. Carstensen for valuable discussions. Furthermore, the author would like to thank the anonymous referees for their suggestions which helped to improve the presentation.

Author information

Authors and Affiliations

  1. Institut für Numerische Simulation, Universität Bonn, Wegelerstraße 6, 53115, Bonn, Germany

    Dietmar Gallistl

Authors
  1. Dietmar Gallistl
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dietmar Gallistl.

Additional information

This work was supported by the DFG Research Center Matheon.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gallistl, D. An optimal adaptive FEM for eigenvalue clusters. Numer. Math. 130, 467–496 (2015). https://doi.org/10.1007/s00211-014-0671-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-014-0671-8

Mathematics Subject Classification