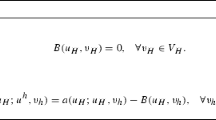We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Skip to main content
Springer Nature Link
Log in

Adaptive boundary element methods for optimal convergence of point errors

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

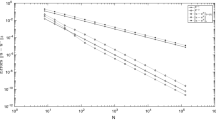
One particular strength of the boundary element method is that it allows for a high-order pointwise approximation of the solution of the related partial differential equation via the representation formula. However, the high-order convergence and hence accuracy usually suffers from singularities of the Cauchy data. We propose two adaptive mesh-refining algorithms and prove their quasi-optimal convergence behavior with respect to an a posteriori computable bound for the point error in the representation formula. Numerical examples for the weakly-singular integral equations for the 2D and 3D Laplacian underline our theoretical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Aurada, M., Ebner, M., Feischl, M., Ferraz-Leite, S., Führer, T., Goldenits, P., Karkulik, M., Mayr, M., Praetorius, D.: HILBERT—a MATLAB implementation of adaptive 2D-BEM. Numer. Algorithms 67(1), 1–32 (2014)

  2. Aurada, M., Feischl, M., Führer, T., Karkulik, M., Praetorius, D.: Efficiency and optimality of some weighted-residual error estimator for adaptive 2D boundary element methods. Comput. Methods Appl. Math. 13(3), 305–332 (2013)

  3. Aurada, M., Feischl, M., Führer, T., Karkulik, M., Melenk, J.M., Praetorius, D.: Local inverse estimates for non-local boundary integral operators. ASC Report 12/2015, University of Technology, Vienna (2015)

  4. Binev, P., Dahmen, W., DeVore, R.: Adaptive finite element methods with convergence rates. Numer. Math. 97(2), 219–268 (2004)

  5. Becker, R., Estecahandy, E., Trujillo, D.: Weighted marking for goal-oriented adaptive finite element methods. SIAM J. Numer. Anal 49(6), 2451–2469 (2011)

  6. Carstensen, C.: An a posteriori error estimate for a first-kind integral equation. Math. Comput. 66(217), 139–155 (1997)

  7. Carstensen, C., Feischl, M., Page, M., Praetorius, D.: Axioms of adaptivity. Comput. Math. Appl. 67(6), 1195–1253 (2014)

  8. Cascon, J.M., Kreuzer, C., Nochetto, R.H., Siebert, K.G.: Quasi-optimal convergence rate for an adaptive finite element method. SIAM J. Numer. Anal. 46(5), 2524–2550 (2008)

  9. Carstensen, C., Maischak, M., Stephan, E.P.: A posteriori error estimate and \(h\)-adaptive algorithm on surfaces for Symm’s integral equation. Numer. Math. 90(2), 197–213 (2001)

  10. Feischl, M., Führer, T., Karkulik, M., Melenk, J.M., Praetorius, D.: Quasi-optimal convergence rates for adaptive boundary element methods with data approximation, part I: weakly-singular integral equation. Calcolo 51, 531–562 (2014)

  11. Feischl, M., Führer, T., Karkulik, M., Melenk, J.M., Praetorius, D.: Quasi-optimal convergence rates for adaptive boundary element methods with data approximation, part II: hyper-singular integral equation. Electron. Trans. Numer. Anal. 44, 153–176 (2015)

  12. Feischl, M., Karkulik, M., Melenk, J.M., Praetorius, D.: Quasi-optimal convergence rate for an adaptive boundary element method. SIAM J. Numer. Anal. 51(2), 1327–1348 (2013)

  13. Gantumur, T.: Adaptive boundary element methods with convergence rates. Numer. Math. 124(3), 471–516 (2013)

  14. Hsiao, G.C., Wendland, W.L.: Boundary integral equations. Springer, Berlin (2008)

    Book  MATH  Google Scholar 

  15. Karkulik, M., Pavlicek, D., Praetorius, D.: On 2D newest vertex bisection: optimality of mesh-closure and \(H^1\)-stability of \(L_2\)-projection. Constr. Approx. 38(2), 213–234 (2013)

  16. McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)

  17. Mommer, M.S., Stevenson, R.: A goal-oriented adaptive finite element method with convergence rates. SIAM J. Numer. Anal. 47(2), 861–886 (2009)

  18. Nochetto, R.H., Veeser, A.: Primer of adaptive finite element methods. In: Naldi, G. (ed.) Multiscale and Adaptivity: Modeling, Numerics and Applications. C.I.M.E. Summer School, Cetraro, Italy, July 6–11, 2009. Lecture Notes in Mathematics, vol. 2040, pp. 125–225 (2012).Springer, Berlin; Fondazione CIME Roberto Conti, Firenze

  19. Smigaj, W., Betcke, T., Arridge, S., Phillips, J., Schweiger, M.: Solving boundary integral problems with BEM\(++\). ACM Trans. Math. Softw. 41, Article #6 (2015)

  20. Sauter, S.A., Schwab, C.: Boundary element methods. Springer, Berlin (2011)

  21. Stevenson, R.: Optimality of a standard adaptive finite element method. Found. Comput. Math. 7(2), 245–269 (2007)

  22. Steinbach, O.: Numerical approximation methods for elliptic boundary value problems–finite and boundary elements. Springer, New York (2008)

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors acknowledge support through the Austrian Science Fund (FWF) under Grant P27005 Optimal adaptivity for BEM and FEM-BEM coupling. MF and DP acknowledge the support of the FWF doctoral school Dissipation and Dispersion in Nonlinear PDEs, funded under Grant W1245. The research of TF is supported by the CONICYT project Preconditioned linear solvers for nonconforming boundary elements, funded under Grant FONDECYT 3150012.

Author information

Authors and Affiliations

  1. Institute for Analysis and Scientific Computing, Vienna University of Technology, Wiedner Hauptstr. 8-10, 1040, Vienna, Austria

    Michael Feischl, Gregor Gantner, Alexander Haberl & Dirk Praetorius

  2. Facultad de Matemáticas, Pontificia Universidad Católica de Chile, Avenida Vicuña Mackenna 4860, Santiago, Chile

    Thomas Führer

Authors
  1. Michael Feischl
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Gregor Gantner
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Alexander Haberl
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Dirk Praetorius
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Thomas Führer
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dirk Praetorius.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Feischl, M., Gantner, G., Haberl, A. et al. Adaptive boundary element methods for optimal convergence of point errors. Numer. Math. 132, 541–567 (2016). https://doi.org/10.1007/s00211-015-0727-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-015-0727-4

Mathematics Subject Classification