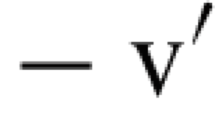Skip to main content
Springer Nature Link
Log in

Hamiltonian B-series and a Lie algebra of non-rooted trees

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

The conditions for a B-series to be a Hamiltonian vector field imply that it may be given as a series indexed by free trees, i.e. trees without root. At present, the pre-Lie structure of rooted trees plays an important role in the study of numerical methods for ordinary differential equations, as does the associated Lie bracket on rooted trees obtained by antisymmetrization. We give a substitute for this Lie bracket defined on free trees that reflects the Lie bracket of Hamiltonian B-series, and illustrate an application of this to the backward error analysis of symplectic numerical integrators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Such coloured B-series are sometimes called NB-series in the literature.

  2. In order to graphically distinguish rooted trees from non-rooted ones, we adopt the following convention: rooted trees are drawn with a fat root, whereas a free tree is represented by one of its rooted representatives, but drawn with a slim root.

References

  1. Araújo, A.L., Murua, A., Sanz-Serna, J.M.: Symplectic methods based on decompositions. SIAM J. Numer. Anal. 34, 1926–1947 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  2. Abia, L., Sanz-Serna, J.M.: Order conditions for canonical Runge–Kutta schemes. SIAM J. Numer. Anal. 28, 1081–1096 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  3. Araujo, A.L., Murua, A., Sanz-Serna, J.-M.: Symplectic methods based on decompositions. SIAM J. Numer. Anal. 34(5), 1926–1947 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  4. Butcher, J.C.: An algebraic theory of integration methods. Math. Comput. 26, 79–106 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  5. Butcher, J.C.: Numerical Methods for Ordinary Differential Equations, 2nd edn. Wiley, Chichester (2008)

    Book  MATH  Google Scholar 

  6. Calvo, M.P., Sanz-Serna, J.M.: Canonical B-series. Numer. Math. 67, 161–175 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cayley, A.: On the theory of the analytical forms called trees. Philos. Mag. 13, 172–176 (1857)

    Google Scholar 

  8. Chapoton, F., Livernet, M.: Pre-Lie algebras and the rooted trees operad. Int. Math. Res. Not. 2001, 395–408 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chartier, Ph, Faou, E., Murua, A.: An algebraic approach to invariant preserving integrators: the case of quadratic and Hamiltonian invariants. Numer. Math. 103, 575–590 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chartier, Ph, Hairer, E., Vilmart, G.: Algebraic structures of B-series. Found. Comput. Math. 10(4), 407–427 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dzhumadil’daev, A., Löfwall, C.: Trees, free right-symmetric algebras, free Novikov algebras and identities. Homol. Homotopy Appl. 4, 165–190 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ebrahimi-Fard, K., Lundervold, A., Munthe-Kaas, H.: On the Lie enveloping algebra of a post-Lie algebra (2014). arXiv:1410.6350 (Preprint)

  13. Hairer, E., Wanner, G.: On the Butcher group and general multi-value methods. Comput. (Arch. Elektron. Rechnen) 13(1), 1–15 (1974)

  14. Hairer, E., Lubich, C., Wanner, G.: Geometric numerical integration. In: Structure-Preserving Algorithms for Ordinary Differential Equations, vol. 31, 2nd edn. Springer Series in Computational Mathematics. Springer, Berlin (2006)

  15. Munthe-Kaas, H., Lundervold, A.: On post-Lie algebras, Lie–Butcher series and moving frames. Found. Comput. Math. 13, 583–613 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  16. Murua, A.: Formal series and numerical integrators. I. Systems of ODEs and symplectic integrators. Appl. Numer. Math. 29(2), 221–251 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  17. Murua, A.: The Hopf algebra of rooted trees, free Lie algebras, and Lie series. Found. Comput. Math. 6, 387–426 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  18. Oudom, J.-M., Guin, D.: On the Lie enveloping algebra of a pre-Lie algebra. J. K-theory 2, 147–167 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  19. Sanz-Serna, J.-M.: Runge–Kutta schemes for Hamiltonian systems. BIT Numer. Anal. 28(4), 877–883 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  20. Sanz-Serna, J.M.: Symplectic integrators for Hamiltonian problems: an overview. Acta Numer. 1, 243–286 (1992)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This article came out from a workshop in December 2012 at NTNU in Trondheim. The authors thank Elena Celledoni, Kurusch Ebrahimi-Fard, Brynjulf Owren and all the participants for illuminating discussions. The third author also thanks Ander Murua and Jesus Sanz-Serna for sharing references and for their encouragements. This work is partly supported by Campus France, PHC Aurora 24678ZC. The third author also acknowledges a support by Agence Nationale de la Recherche (projet CARMA). We thank the referees for pertinent remarks which greatly helped us to improve the redaction of the article.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, NTNU, 7491, Trondheim, Norway

    Geir Bogfjellmo & Charles Curry

  2. Université Blaise Pascal, C.N.R.S.-UMR 6620, CS 60026, 3 place Vasarély, 63178, Aubière, France

    Dominique Manchon

Authors
  1. Geir Bogfjellmo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Charles Curry
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Dominique Manchon
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dominique Manchon.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bogfjellmo, G., Curry, C. & Manchon, D. Hamiltonian B-series and a Lie algebra of non-rooted trees. Numer. Math. 135, 97–112 (2017). https://doi.org/10.1007/s00211-016-0792-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-016-0792-3

Mathematics Subject Classification